Як виконати множинну лінійну регресію в spss

Множинна лінійна регресія — це метод, який ми можемо використовувати для розуміння зв’язку між двома або більше пояснювальними змінними та змінною відповіді.

У цьому посібнику пояснюється, як виконувати множинну лінійну регресію в SPSS.

Приклад: Множинна лінійна регресія в SPSS

Припустімо, ми хочемо знати, чи впливає кількість годин, витрачених на навчання, і кількість складених практичних іспитів на оцінку, яку студент отримує на даному іспиті. Щоб дослідити це, ми можемо виконати множинну лінійну регресію, використовуючи такі змінні:

Пояснювальні змінні:

• Вивчені години
• Підготовчі іспити складено

Змінна відповіді:

• Результат іспиту

Виконайте наступні кроки, щоб виконати цю множинну лінійну регресію в SPSS.

Крок 1: Введіть дані.

Про кількість вивчених годин, складених підготовчих іспитів та отриманих результатів іспитів для 20 студентів введіть такі дані:

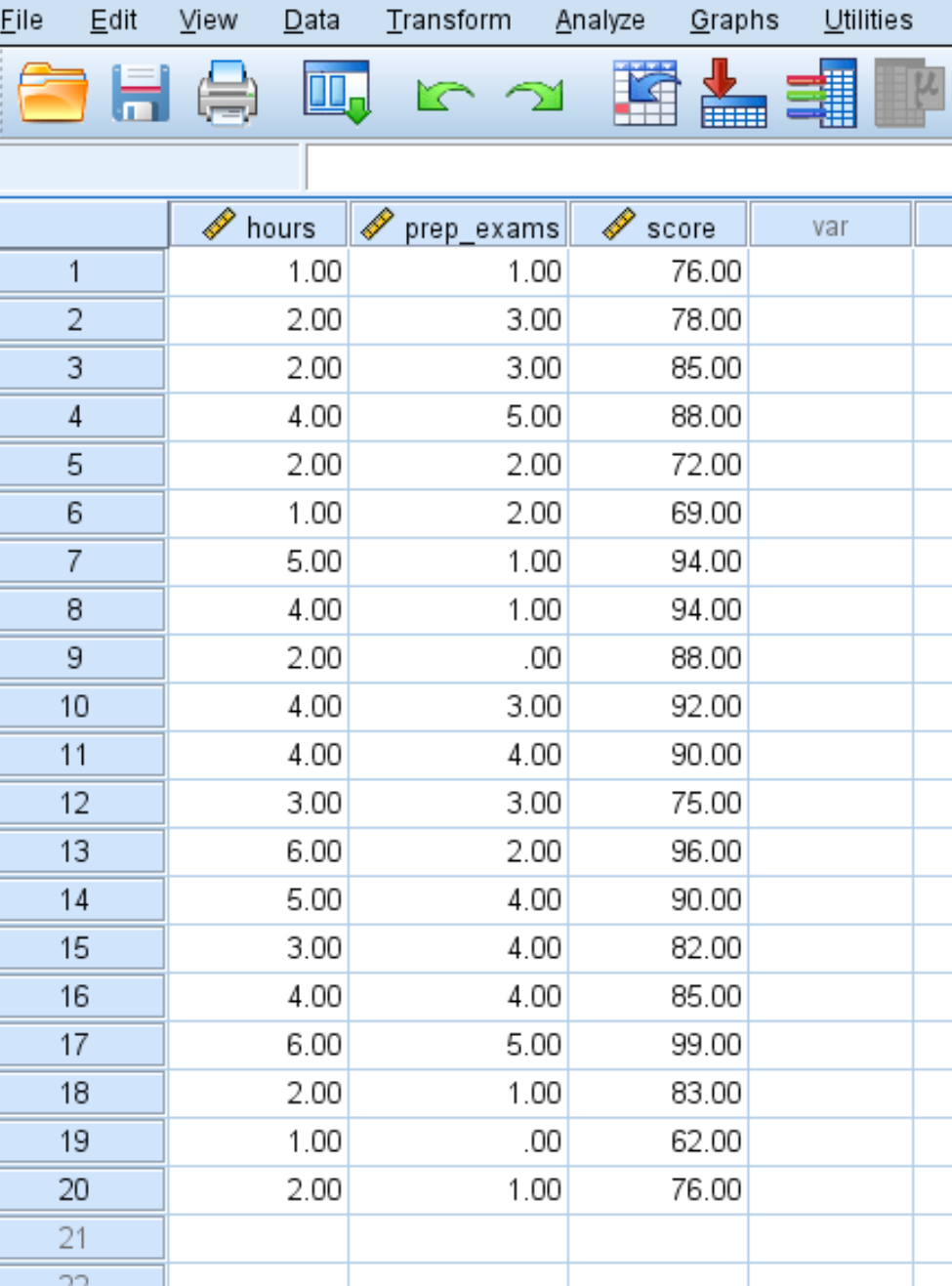
Крок 2: Виконайте множинну лінійну регресію.

Натисніть вкладку «Аналіз» , потім «Регресія» , потім «Лінійна» :

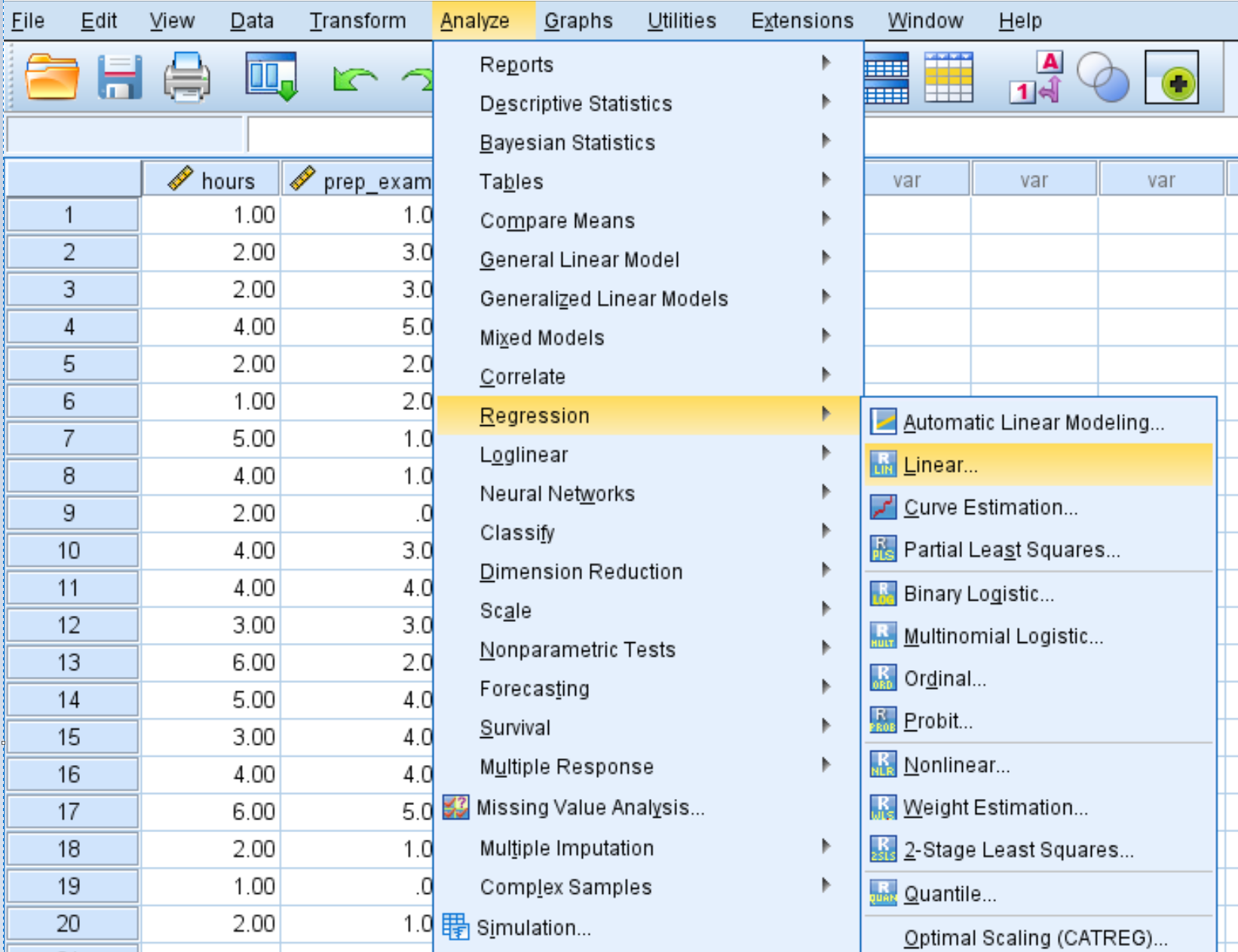
Перетягніть оцінку змінної в поле з позначкою «Залежна». Перетягніть змінні години та prep_exams у поле з позначкою Independent(s). Потім натисніть OK .

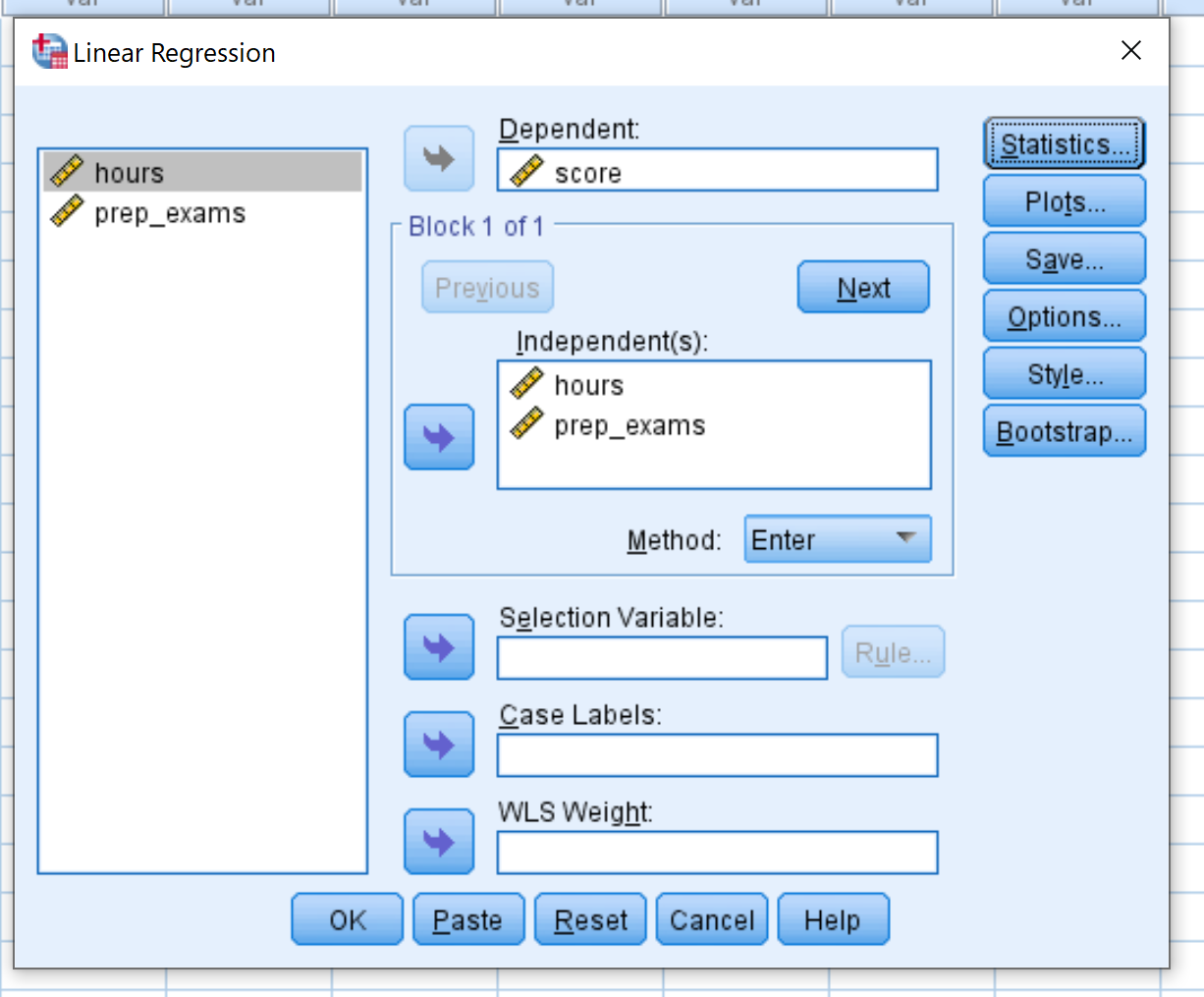
Крок 3: Інтерпретація результату.

Після натискання кнопки OK результати множинної лінійної регресії з’являться в новому вікні.

Перша таблиця, яка нас цікавить, називається «Підсумок моделі» :

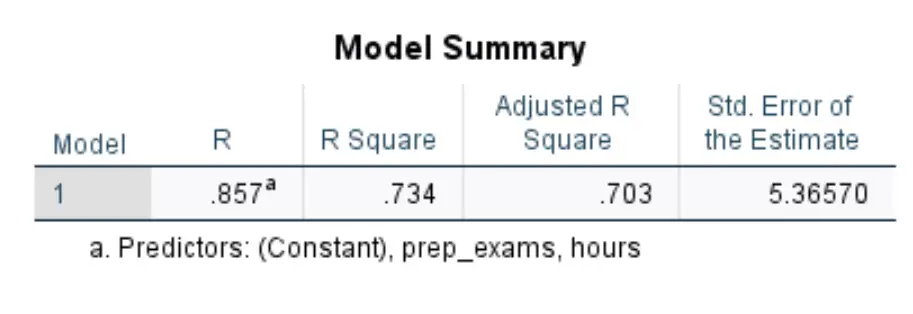
Ось як інтерпретувати найбільш відповідні цифри в цій таблиці:

• R Square: це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальними змінними. У цьому прикладі 73,4% варіації оцінок за іспит можна пояснити вивченими годинами та кількістю складених підготовчих іспитів.
• Стандартний. Похибка оцінки: стандартна помилка – це середня відстань між спостережуваними значеннями та лінією регресії. У цьому прикладі спостережувані значення відхиляються в середньому на 5,3657 одиниць від лінії регресії.

Наступна таблиця, яка нас цікавить, називається ANOVA :

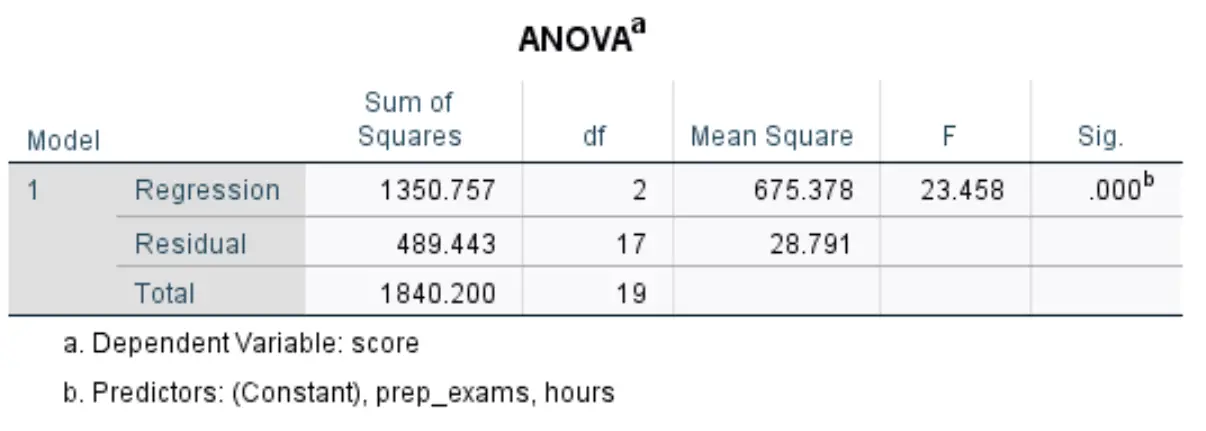
Ось як інтерпретувати найбільш відповідні цифри в цій таблиці:

• F: це загальна F-статистика для регресійної моделі, розрахована як середньоквадратична регресія / середньоквадратичний залишок.
• Sig: це p-значення, пов’язане із загальною статистикою F. Це говорить нам про те, чи є модель регресії в цілому статистично значущою чи ні. Іншими словами, це повідомляє нам, чи дві пояснювальні змінні разом мають статистично значущий зв’язок зі змінною відповіді. У цьому випадку p-значення дорівнює 0,000, що вказує на те, що пояснювальні змінні, вивчені години та складені підготовчі іспити, мають статистично значущий зв’язок із результатом іспиту.

Наступна таблиця, яка нас цікавить, має назву Коефіцієнти :

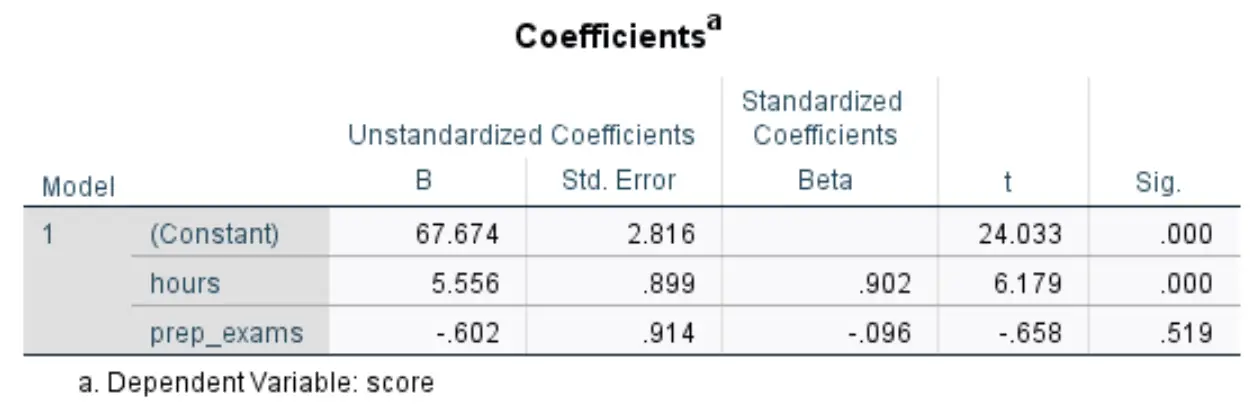
Ось як інтерпретувати найбільш відповідні цифри в цій таблиці:

• B нестандартизована (постійна): це повідомляє нам про середнє значення змінної відповіді, коли обидві змінні предиктора дорівнюють нулю. У цьому прикладі середній бал за іспит становить 67 674 , коли навчальні години та підготовчі іспити дорівнюють нулю.
• Нестандартизований B (годин): це вказує нам на середню зміну балів за іспит, пов’язану зі збільшенням навчальних годин на одну одиницю, припускаючи, що кількість складених підготовчих іспитів залишається постійною. У цьому випадку кожна додаткова година, витрачена на навчання, пов’язана зі збільшенням оцінки іспиту на 5556 балів, якщо припустити, що кількість складених практичних іспитів залишається постійною.
• Нестандартизований B (prep_exams): Це повідомляє нам про середню зміну оцінки іспиту, пов’язану зі збільшенням на одну одиницю кількості складених підготовчих іспитів, припускаючи, що кількість вивчених годин залишається постійною. У цьому випадку кожен додатковий складений підготовчий іспит пов’язаний зі зниженням оцінки іспиту на 0,602 бала, припускаючи, що кількість вивчених годин залишається постійною.
• Sig. (години): Це p-значення для пояснювальної змінної годин . Оскільки це значення (0,000) менше 0,05, ми можемо зробити висновок, що вивчені години мають статистично значущий зв’язок з оцінками іспиту.
• Sig. (prep_exams): це p-значення для пояснювальної змінної prep_exams . Оскільки це значення (0,519) не менше 0,05, ми не можемо зробити висновок, що кількість складених підготовчих іспитів має статистично значущий зв’язок із результатом іспиту.

Нарешті, ми можемо сформувати рівняння регресії, використовуючи значення, наведені в таблиці для постійних , годин і prep_exams . У цьому випадку рівняння буде таким:

Приблизний бал за іспит = 67,674 + 5,556*(годин) – 0,602*(підготовчі іспити)

Ми можемо використати це рівняння, щоб знайти приблизний бал студента за іспит на основі кількості годин навчання та кількості практичних іспитів, які вони склали. Наприклад, студент, який навчається 3 години і складає 2 підготовчі іспити, повинен отримати іспитовий бал 83,1:

Приблизний бал за іспит = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Примітка. Оскільки пояснювальна змінна для підготовчих іспитів не виявилася статистично значущою, ми можемо вирішити видалити її з моделі та замість цього виконати просту лінійну регресію , використовуючи досліджувані години як єдину пояснювальну змінну.