Як створити та інтерпретувати криву roc у spss

Логістична регресія – це статистичний метод, який ми використовуємо для підгонки регресійної моделі, коли змінна відповіді є двійковою. Щоб оцінити, наскільки модель логістичної регресії відповідає набору даних, ми можемо розглянути такі два показники:

• Чутливість: ймовірність того, що модель передбачає позитивний результат для спостереження, коли результат насправді позитивний.
• Специфічність: ймовірність того, що модель передбачає негативний результат для спостереження, коли результат насправді негативний.

Простим способом візуалізації цих двох показників є створення кривої ROC , яка є графіком, що відображає чутливість і специфічність моделі логістичної регресії.

Цей підручник пояснює, як створити та інтерпретувати криву ROC у SPSS.

Приклад: крива ROC у SPSS

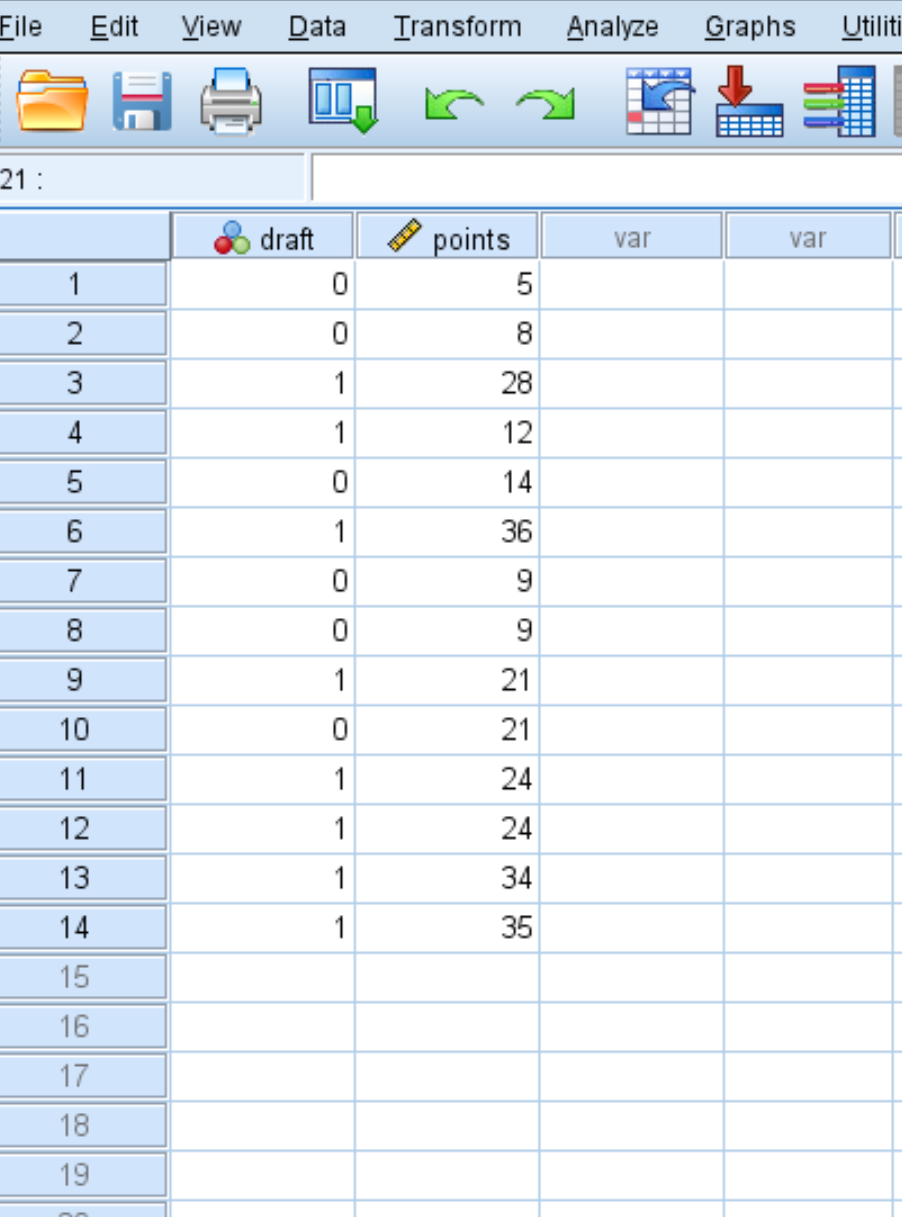
Припустимо, у нас є такий набір даних, який показує, чи був баскетболіст задрафтований до НБА (0 = ні, 1 = так), а також його середню кількість очок за гру в коледжі:

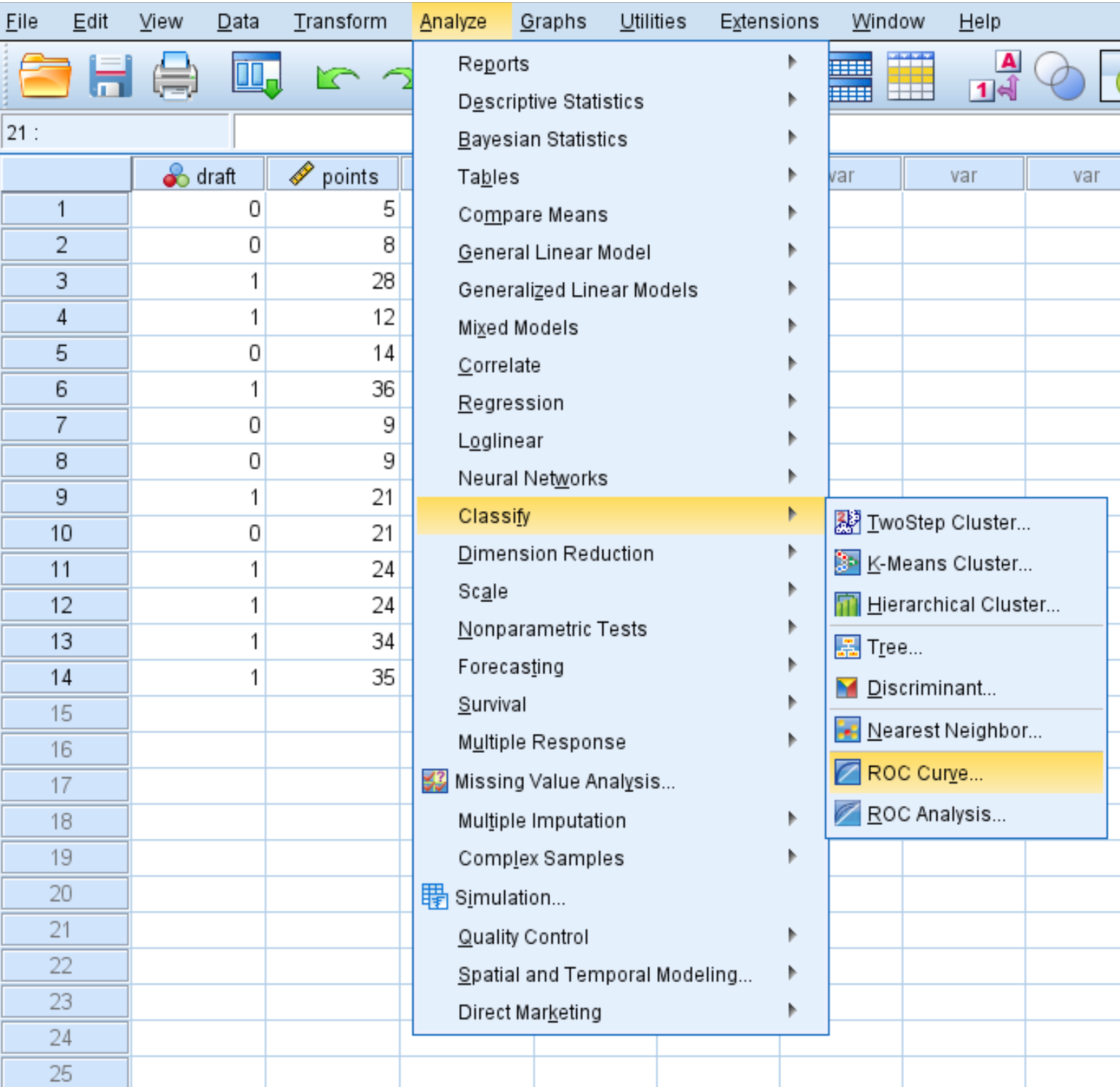
Щоб створити криву ROC для цього набору даних, клацніть вкладку Analyze , потім Classify , а потім ROC Curve :

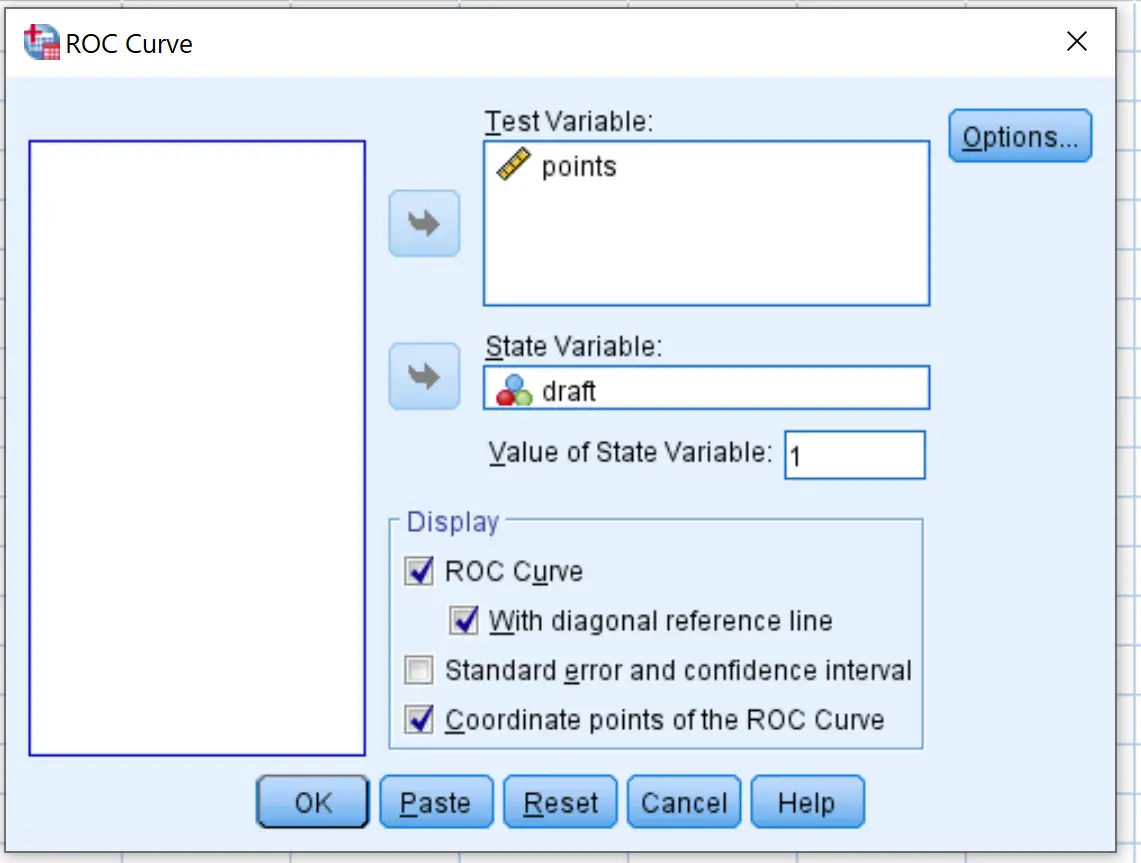
У новому вікні, що з’явиться, перетягніть чернетку змінної в область під назвою «Змінна стану». Встановіть значення змінної стану на 1 . (Це значення вказує на те, що гравця обрано). Перетягніть точки змінної в область під назвою «Тестова змінна».

Поставте прапорці поруч із пунктами «З діагональною опорною лінією та координатами точки кривої ROC» . Потім натисніть OK .

Ось як інтерпретувати результат:

Підсумок обробки файлів:

Ця таблиця відображає загальну кількість позитивних і негативних випадків у наборі даних. У цьому прикладі 8 гравців були задрафтовані (позитивний результат) і 6 гравців не були задрафтовані (негативний результат):

Крива ROC:

Крива робочих характеристик приймача (ROC) є графіком значень чутливості проти специфічності 1, коли порогове значення змінюється від 0 до 1:

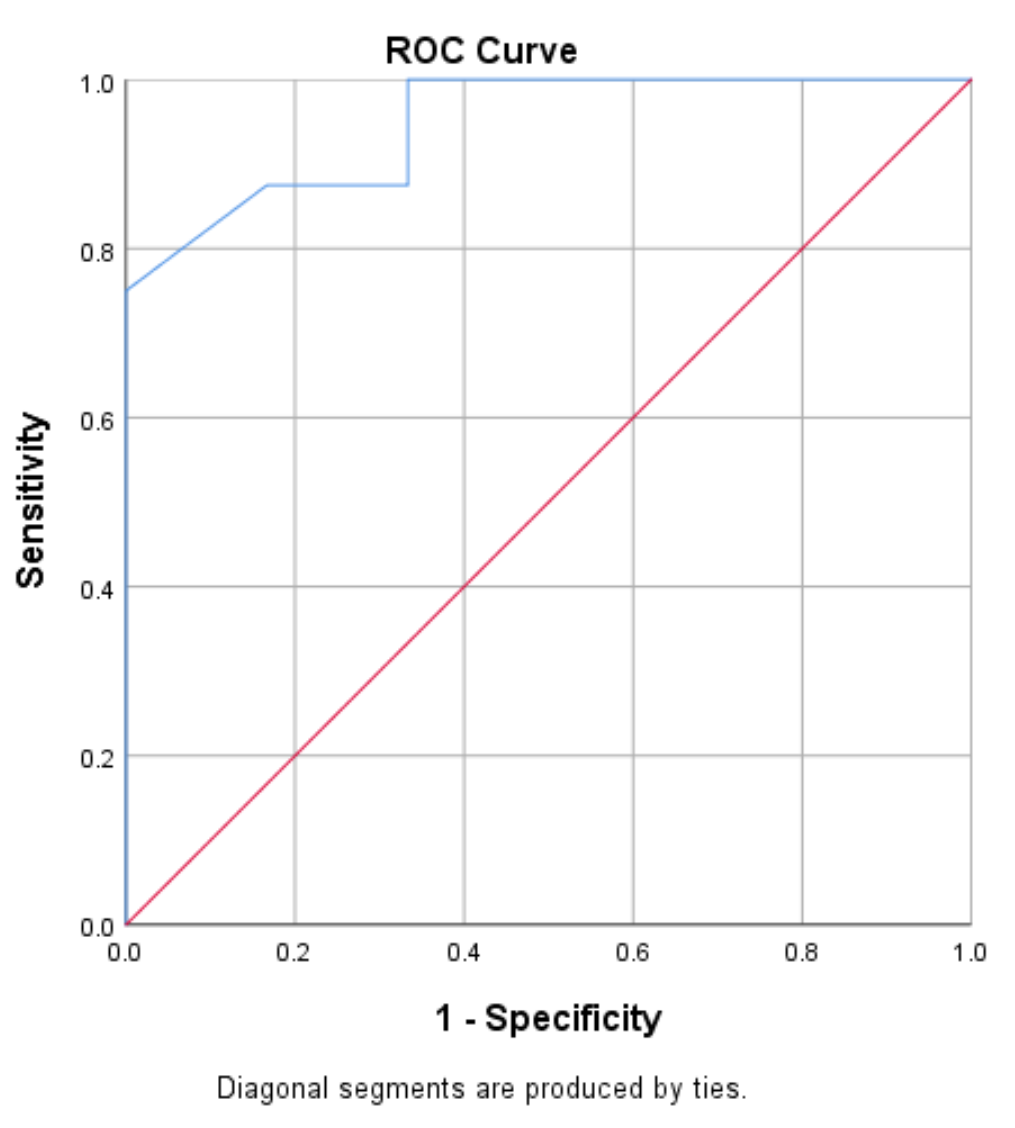
Модель з високою чутливістю та специфічністю матиме криву ROC, яка відповідає верхньому лівому куту графіка. Модель з низькою чутливістю та низькою специфічністю матиме криву, близьку до діагоналі 45 градусів.

Ми бачимо, що крива ROC (синя лінія) у цьому прикладі обіймає верхній лівий кут графіка, вказуючи на те, що модель добре справляється з прогнозуванням гравців, які будуть обрані чи ні, на основі їхніх середніх очок за гру . .

Площа під кривою:

Площа під кривою дає нам уявлення про здатність моделі розрізняти позитивні та негативні результати. AUC може коливатися від 0 до 1. Що вищий AUC, то краще модель правильно класифікує результати.

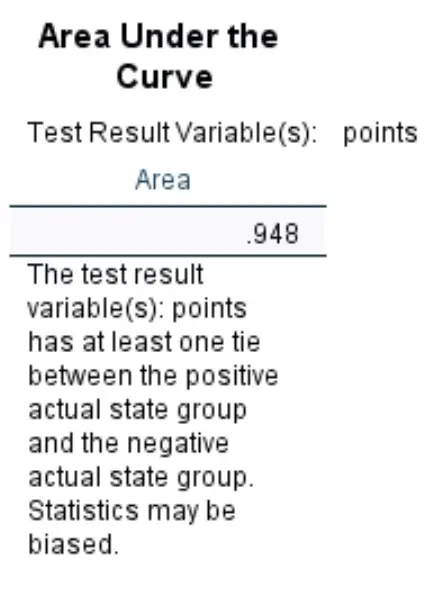
Ми бачимо, що AUC для цієї моделі логістичної регресії становить 0,948 , що є надзвичайно високим показником. Це вказує на те, що модель добре справляється з прогнозуванням того, буде гравець обраний чи ні.

Координати кривої:

Ця остання таблиця відображає чутливість і специфічність 1 кривої ROC для різних порогів.

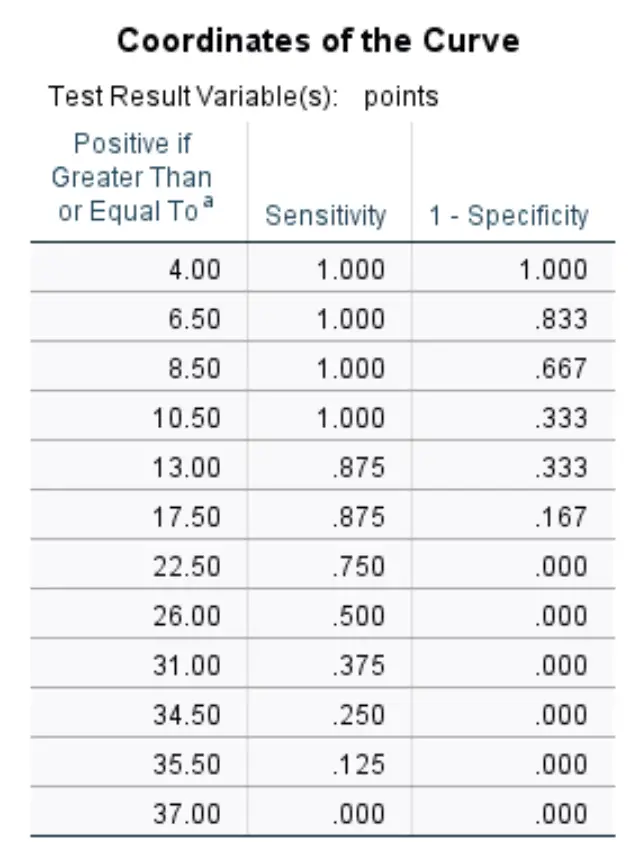
Наприклад:

Якщо ми дозволимо поріг становити 8,50 , це означає, що ми очікуємо, що будь-який гравець, який набере менше 8,50 очок за гру, не буде обраний, і що будь-який гравець, який набере більше 8,50 очок за гру, буде обраний.

Використовуючи це як порогове значення, наша чутливість становитиме 100% (оскільки кожен гравець, який набрав менше 8,50 очок за гру, справді не був задрафтований), а наша специфічність 1 становитиме 66,7% (оскільки 8 гравців із 12 набрали більше 8,50 очок за гру були драфтовані).

Наведена вище таблиця дозволяє нам побачити чутливість і специфічність 1 для кожного потенційного порогу.