Як виконати просту лінійну регресію в spss

Проста лінійна регресія — це метод, який ми можемо використати для розуміння зв’язку між змінною предиктором і змінною відповіді.

У цьому посібнику пояснюється, як виконати просту лінійну регресію в SPSS.

Приклад: проста лінійна регресія в SPSS

Скажімо, у нас є такий набір даних, який показує кількість вивчених годин і оцінку іспиту, отриману 20 студентами:

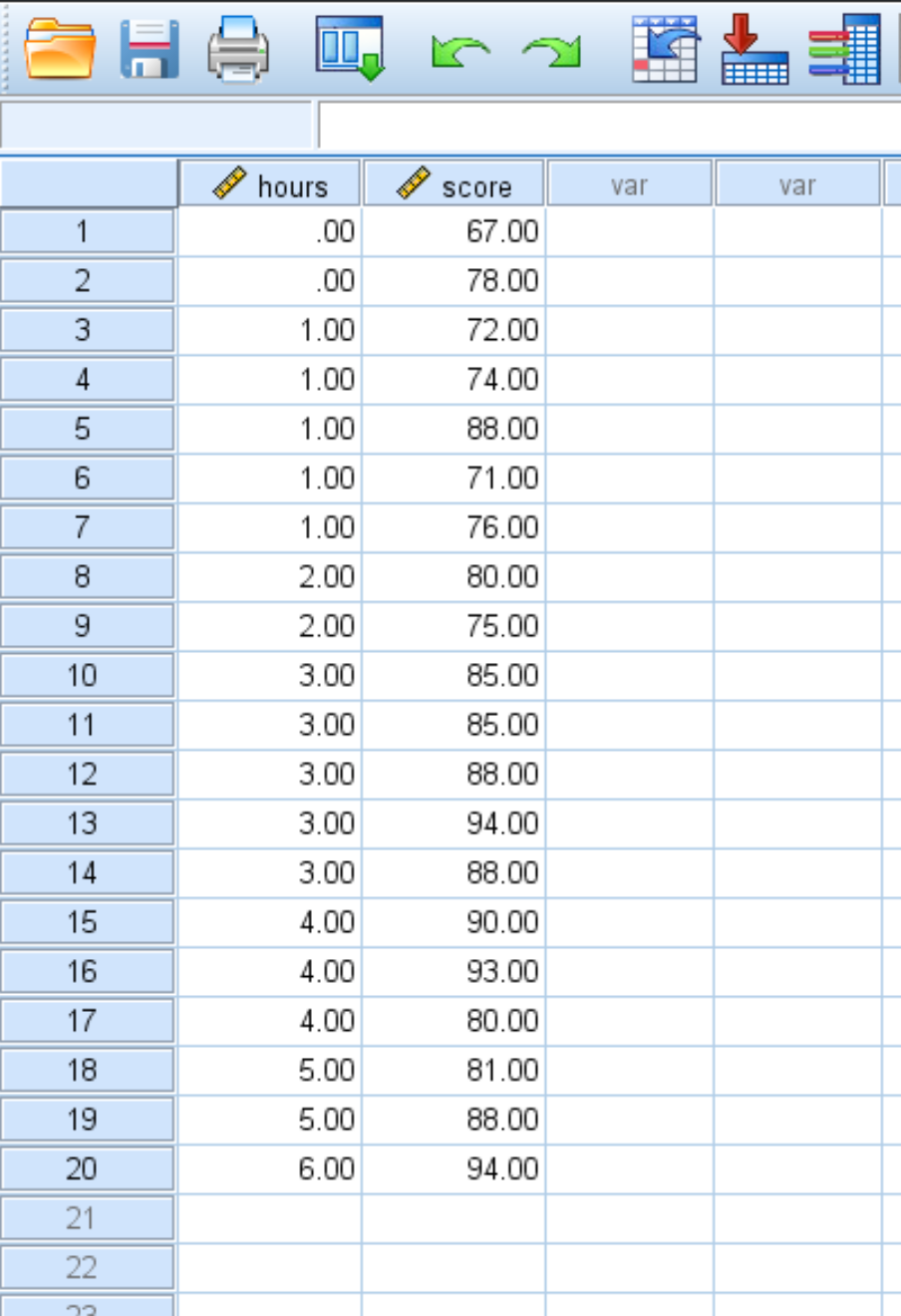
Виконайте наведені нижче кроки, щоб виконати просту лінійну регресію на цьому наборі даних, щоб кількісно визначити зв’язок між годинами вивчення та результатом іспиту:

Крок 1: Візуалізуйте дані.

По-перше, ми створимо діаграму розсіювання, щоб візуалізувати зв’язок між годинами та оцінкою, щоб переконатися, що зв’язок між двома змінними виглядає лінійним. Інакше проста лінійна регресія не буде відповідним методом для використання.

Перейдіть на вкладку «Діаграми» , а потім клацніть «Конструктор діаграм ».

У меню «Вибрати з» клацніть і перетягніть Scatter/Dot у головне вікно редагування. Потім перетягніть змінний час на вісь X, а оцінку на вісь Y.

Після натискання кнопки OK з’явиться така діаграма розсіювання:

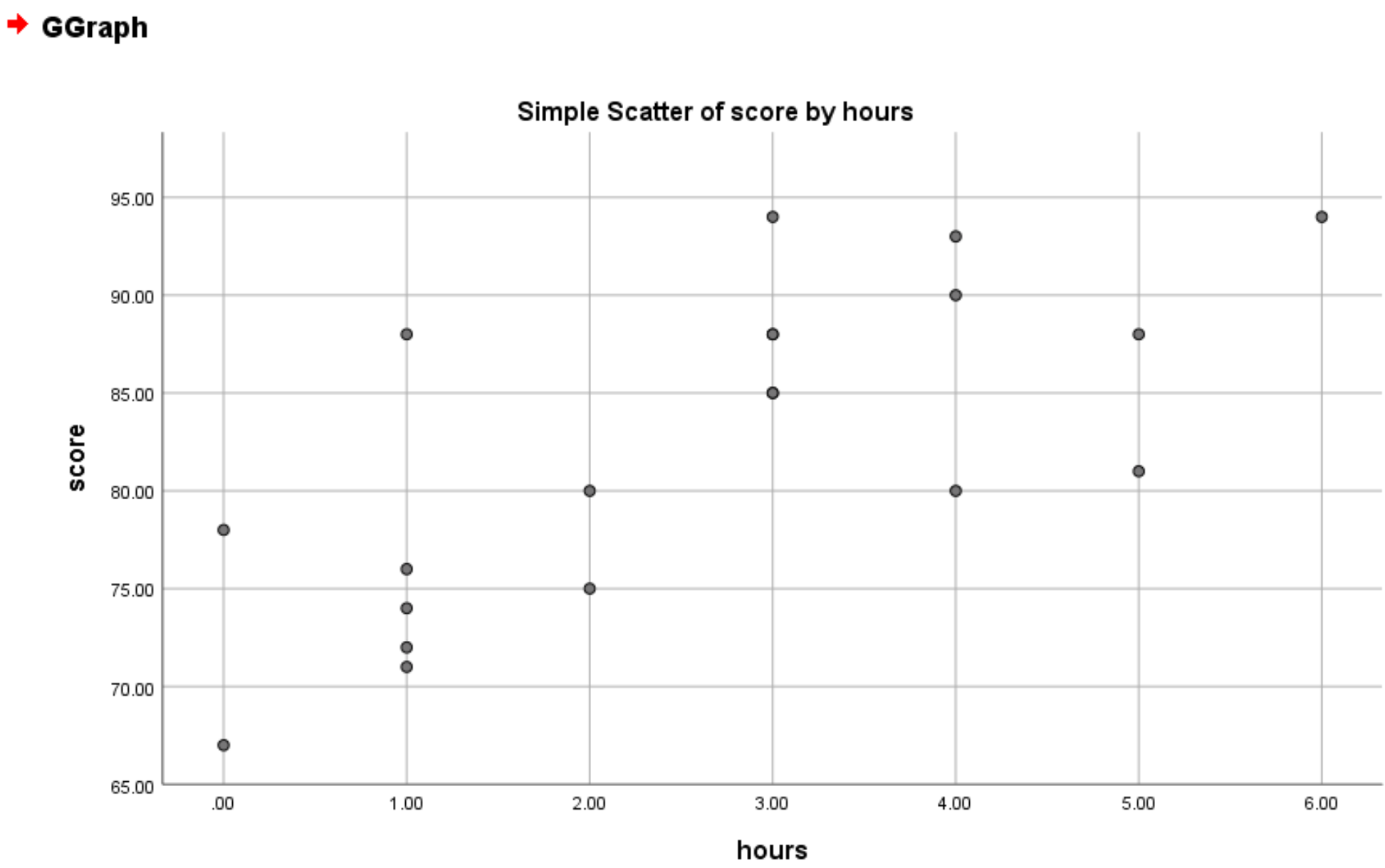
З графіка ми бачимо, що існує позитивна лінійна залежність між годинами та результатами. Загалом студенти, які навчаються більше годин, як правило, мають вищі бали.

Оскільки існує чіткий лінійний зв’язок між двома змінними, ми продовжимо адаптувати просту модель лінійної регресії до набору даних.

Крок 2. Підберіть просту модель лінійної регресії.

Натисніть вкладку «Аналіз» , потім «Регресія» , потім «Лінійна» :

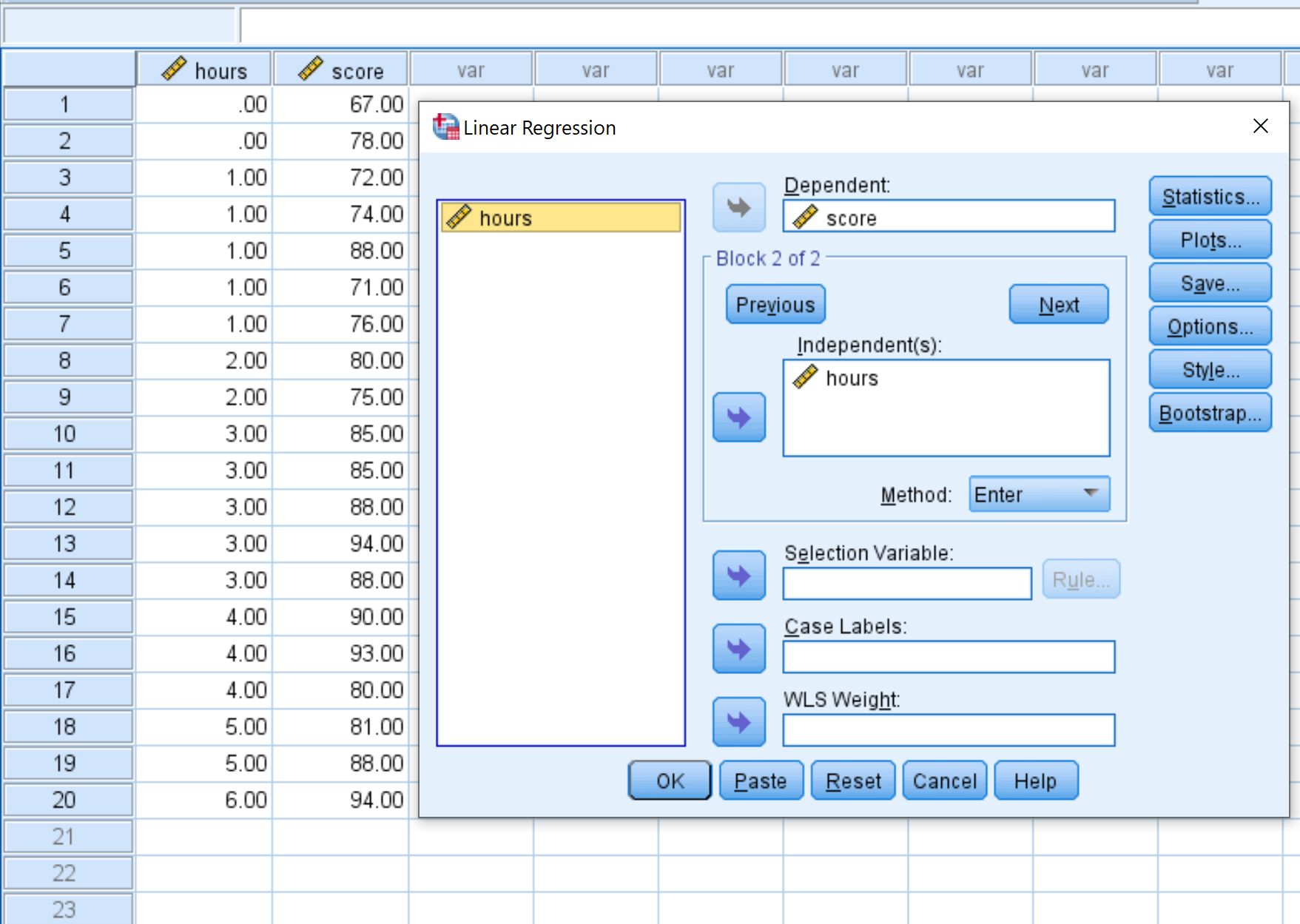
У новому вікні, що з’явиться, перетягніть змінну оцінку в поле з позначкою «Залежний» і перетягніть години в поле з позначкою «Незалежне». Потім натисніть OK .

Крок 3: Інтерпретація результатів.

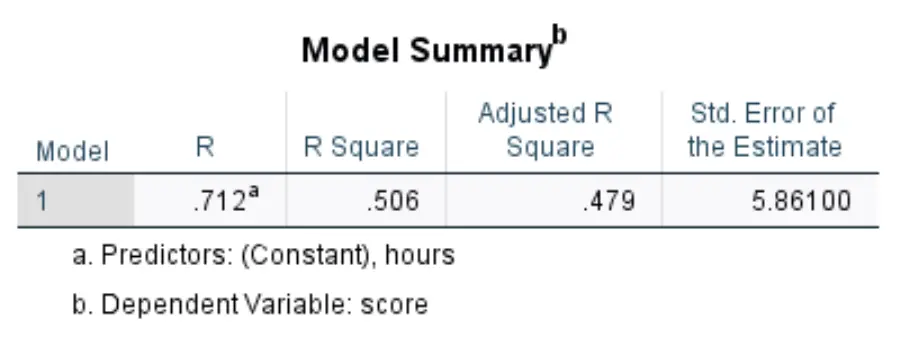
Після натискання кнопки OK з’являться результати простої лінійної регресії. Перша таблиця, яка нас цікавить, це таблиця під назвою «Резюме моделі» :

Ось як інтерпретувати найбільш відповідні цифри в цій таблиці:

• R Square: це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальною змінною. У цьому прикладі 50,6% варіації оцінок на іспитах можна пояснити кількістю вивчених годин.
• Стандартний. Похибка оцінки: стандартна помилка – це середня відстань між спостережуваними значеннями та лінією регресії. У цьому прикладі спостережувані значення відхиляються в середньому на 5861 одиницю від лінії регресії.

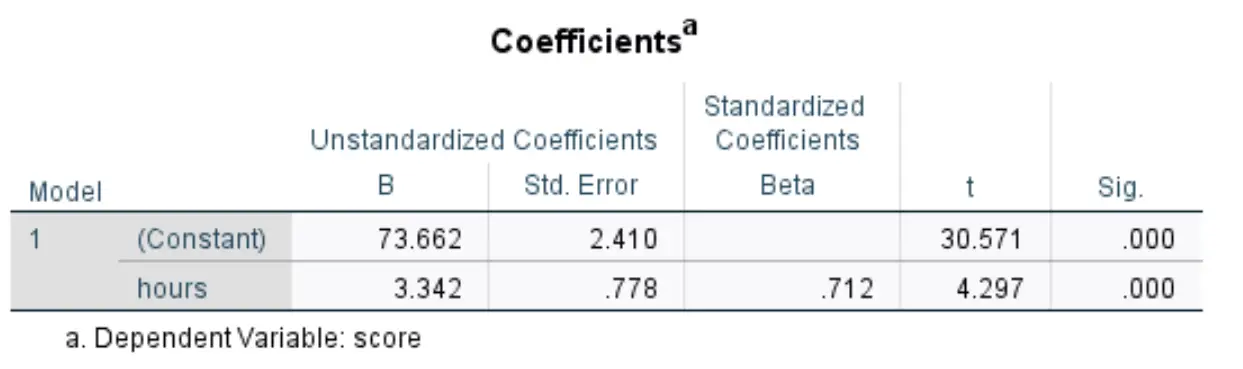
Наступна таблиця, яка нас цікавить, має назву Коефіцієнти :

Ось як інтерпретувати найбільш відповідні цифри в цій таблиці:

• Нестандартизований B (константа) : Це повідомляє нам про середнє значення змінної відповіді , коли змінна предиктора дорівнює нулю. У цьому прикладі середній бал іспиту становить 73,662 , коли вивчені години дорівнюють нулю.
• B нестандартизований (годин): це повідомляє нам про середню зміну змінної відповіді, пов’язану зі збільшенням на одну одиницю змінної предиктора. У цьому прикладі кожна додаткова вивчена година пов’язана зі збільшенням оцінки іспиту в середньому на 3342 .
• Sig (години): це p-значення , пов’язане зі статистикою тесту протягом годин. У цьому випадку, оскільки це значення менше 0,05, ми можемо зробити висновок, що прогностична змінна годин є статистично значущою.

Нарешті, ми можемо сформувати рівняння регресії, використовуючи значення константи та години . У цьому випадку рівняння буде таким:

Орієнтовний бал за іспит = 73,662 + 3,342*(години)

Ми можемо використати це рівняння, щоб знайти приблизний бал студента за іспит на основі кількості вивчених годин.

Наприклад, студент, який навчається 3 години, повинен набрати іспитовий бал 83,688:

Розрахунковий бал за іспит = 73,662 + 3,342*(3) = 83,688

Крок 4: Повідомте про результати.

Нарешті, ми хочемо підсумувати результати нашої простої лінійної регресії. Ось приклад того, як це зробити:

Просту лінійну регресію було виконано для кількісного визначення зв’язку між вивченими годинами та оцінкою іспиту. Для аналізу була використана вибірка з 20 студентів.

Результати показали, що існує статистично значущий зв’язок між вивченими годинами та оцінкою іспиту (t = 4,297, p < 0,000), і що витрачені години становлять 50,6% поясненої мінливості оцінки іспиту. екзамен.

Рівняння регресії вийшло таким:

Орієнтовний бал за іспит = 73,662 + 3,342*(години)

Кожна додаткова вивчена година пов’язана зі збільшенням оцінки іспиту в середньому на 3342 .

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в SPSS:

Як виконати множинну лінійну регресію в SPSS
Як виконати квадратичну регресію в SPSS
Як виконати логістичну регресію в SPSS