Короткий посібник із суми квадратів: sst, ssr, sse
Лінійна регресія використовується для пошуку лінії, яка найкраще «відповідає» набору даних.
Ми часто використовуємо три різні суми квадратів , щоб визначити, наскільки лінія регресії відповідає даним:
1. Сума загальних квадратів (SST) – сума квадратів різниць між окремими точками даних (y i ) і середнім значенням змінної відповіді ( y ).
- SST = Σ(y i – y ) 2
2. Сума квадратів регресії (SSR) – сума квадратів різниць між прогнозованими точками даних (ŷ i ) і середнім значенням змінної відповіді ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Помилка суми квадратів (SSE) – сума квадратів різниць між прогнозованими точками даних (ŷ i ) і спостережуваними точками даних (y i ).
- SSE = Σ(ŷ i – y i ) 2
Між цими трьома показниками існує такий зв’язок:
SST = SSR + SSE
Отже, якщо ми знаємо два з цих вимірювань, ми можемо використовувати просту алгебру для обчислення третього.
ССР, ССТ і Р-пл
R-квадрат , який іноді називають коефіцієнтом детермінації, є показником того, наскільки модель лінійної регресії відповідає набору даних. Він представляє частку дисперсії у змінній відповіді , яку можна пояснити змінною предиктора.
Значення R-квадрат може коливатися від 0 до 1. Значення 0 вказує на те, що змінна відповіді взагалі не може бути пояснена змінною предиктора. Значення 1 вказує на те, що змінна відповіді може бути ідеально пояснена безпомилково змінною предиктора.
Використовуючи SSR і SST, ми можемо обчислити R у квадраті наступним чином:
R у квадраті = SSR / SST
Наприклад, якщо SSR для даної регресійної моделі дорівнює 137,5, а SST — 156, ми розрахуємо R у квадраті таким чином:
R у квадраті = 137,5 / 156 = 0,8814
Це говорить нам про те, що 88,14% варіації змінної відповіді можна пояснити змінною предиктора.
Розрахунок SST, SSR, SSE: покроковий приклад
Припустімо, що ми маємо такий набір даних, який показує кількість годин, вивчених шістьма різними студентами, а також їхні підсумкові іспити:
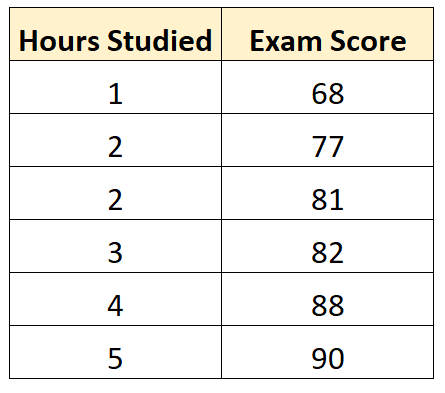
Використовуючи деяке статистичне програмне забезпечення (наприклад, R , Excel , Python ) або навіть вручну, ми можемо побачити, що найкращий рядок:
Оцінка = 66,615 + 5,0769*(години)
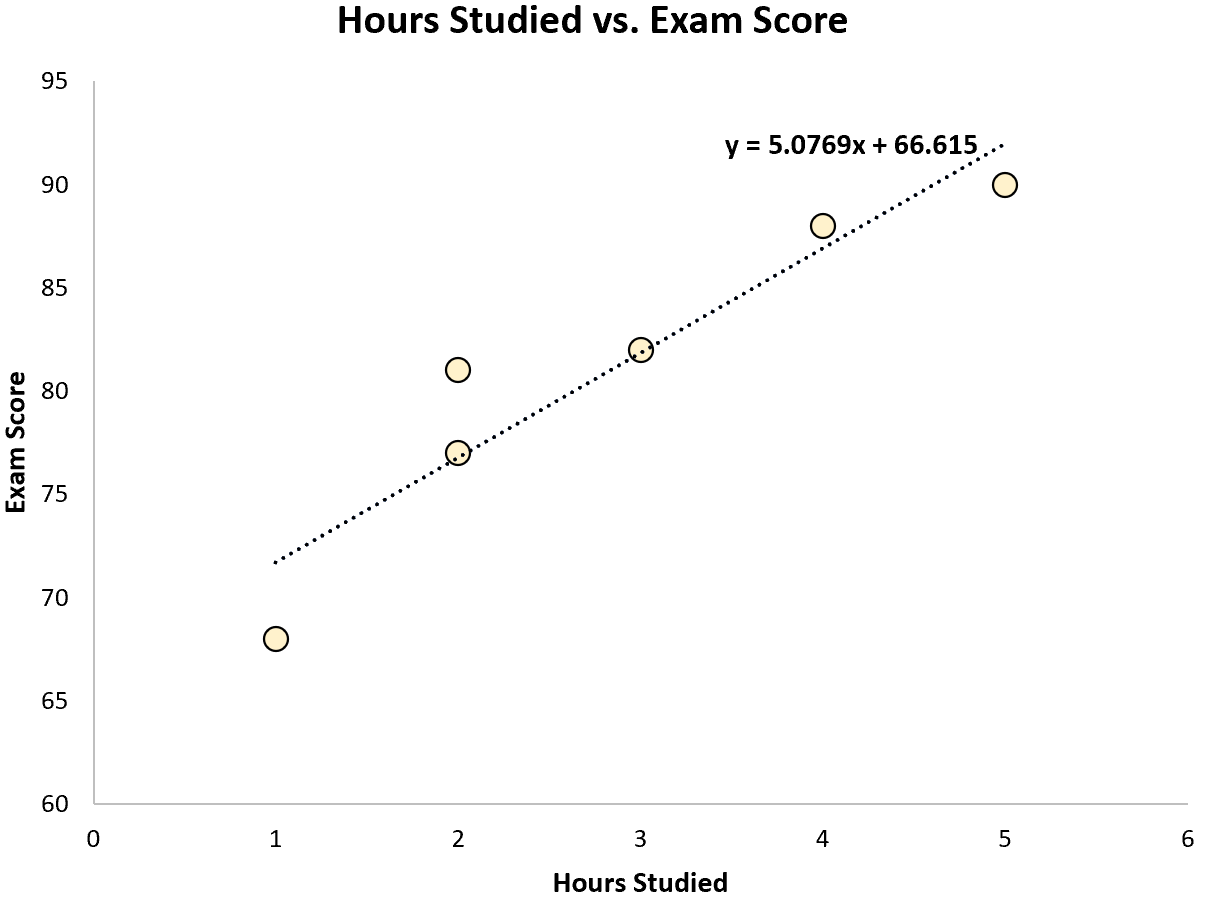
Коли ми знаємо лінію рівняння найкращого підходу, ми можемо використати наступні кроки для розрахунку SST, SSR і SSE:
Крок 1: Обчисліть середнє значення змінної відповіді.
Середнє значення змінної відповіді ( y ) виявляється рівним 81 .
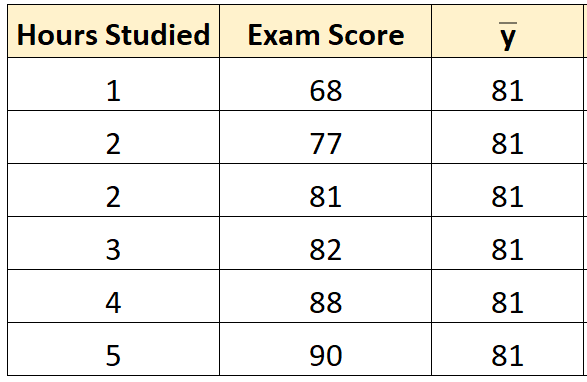
Крок 2: Обчисліть прогнозоване значення для кожного спостереження.
Тоді ми можемо використати рядок рівняння найкращого підходу, щоб обчислити прогнозований бал за іспит () для кожного студента.
Наприклад, прогнозована оцінка іспиту для студента, який навчався одну годину, становить:
Оцінка = 66,615 + 5,0769*(1) = 71,69 .
Ми можемо використати той самий підхід, щоб знайти прогнозований бал для кожного студента:
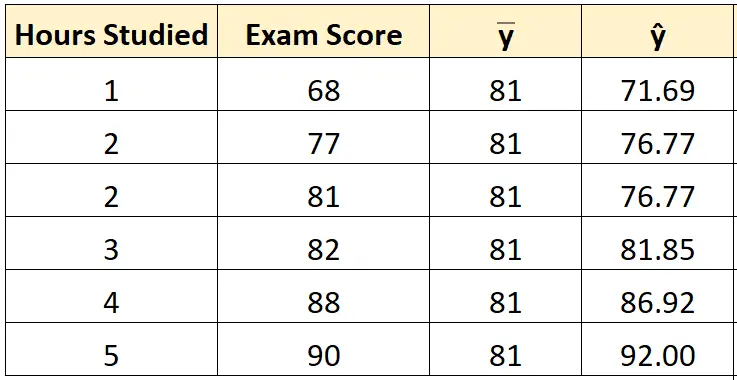
Крок 3: обчисліть загальну суму квадратів (SST).
Тоді ми можемо обчислити загальну суму квадратів.
Наприклад, загальна сума квадратів для першого учня:
(y i – y ) 2 = (68 – 81) 2 = 169 .
Ми можемо використати той самий підхід, щоб знайти загальну суму квадратів для кожного студента:
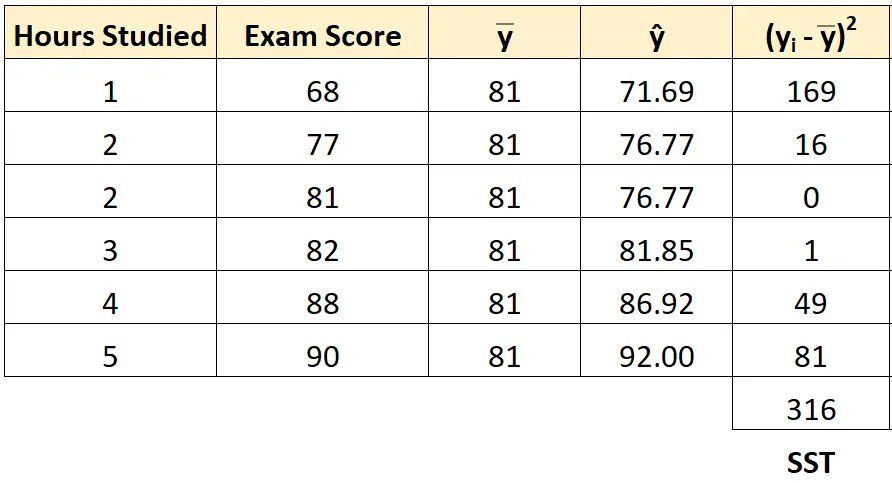
Загальна сума квадратів виявляється 316 .
Крок 4: Обчисліть регресію суми квадратів (SSR).
Тоді ми можемо обчислити суму квадратів регресії.
Наприклад, сума квадратів регресії для першого студента дорівнює:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
Ми можемо використати той самий підхід, щоб знайти регресію суми квадратів для кожного студента:
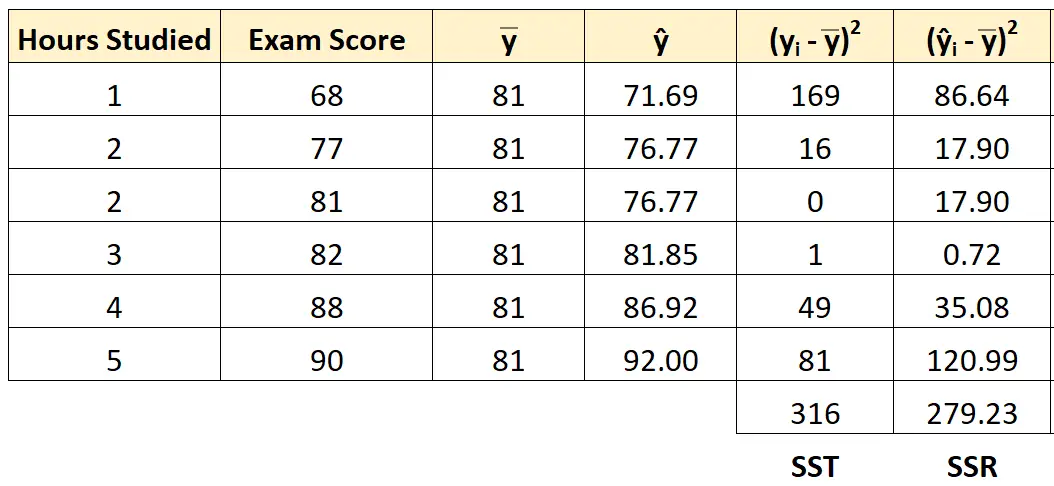
Сума квадратів регресії дорівнює 279,23 .
Крок 5. Обчисліть похибку суми квадратів (SSE).
Тоді можна обчислити похибку суми квадратів.
Наприклад, похибка суми квадратів для першого учня дорівнює:
(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .
Ми можемо використати той самий підхід, щоб знайти помилку суми квадратів для кожного студента:
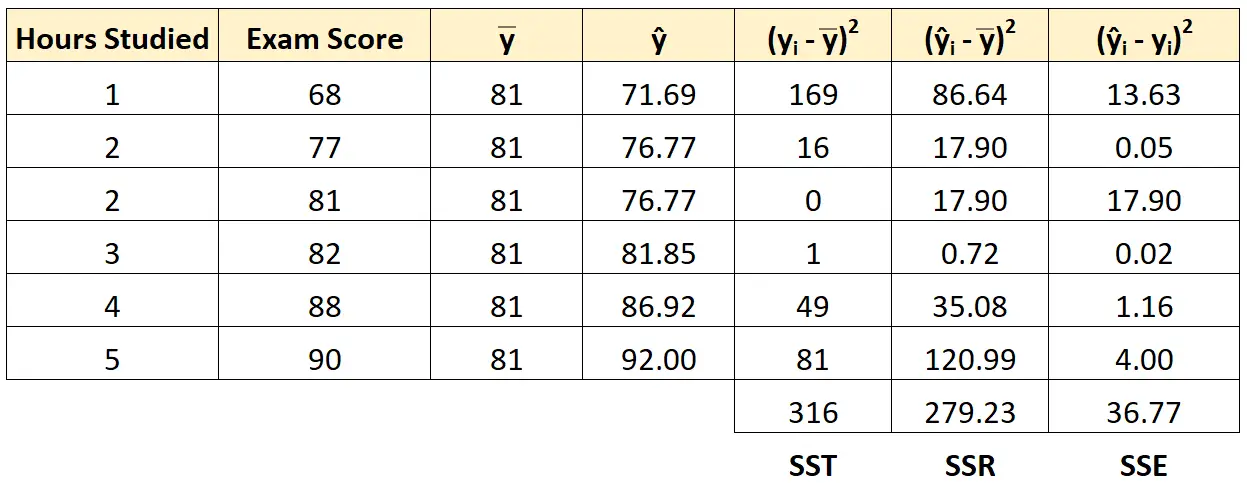
Ми можемо перевірити, що SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Ми також можемо обчислити квадрат R регресійної моделі за допомогою такого рівняння:
- R у квадраті = SSR / SST
- R у квадраті = 279,23 / 316
- R у квадраті = 0,8836
Це говорить нам про те, що 88,36% варіації оцінок на іспитах можна пояснити кількістю вивчених годин.
Додаткові ресурси
Ви можете використовувати такі калькулятори для автоматичного обчислення SST, SSR і SSE для будь-якої простої лінії лінійної регресії:
Калькулятор SST
RSS калькулятор
Калькулятор ESS
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше