Як розрахувати sst, ssr і sse в excel
Ми часто використовуємо три різні суми квадратів , щоб визначити, наскільки лінія регресії відповідає набору даних:
1. Сума загальних квадратів (SST) – сума квадратів різниць між окремими точками даних (y i ) і середнім значенням змінної відповіді ( y ).
- SST = Σ(y i – y ) 2
2. Сума квадратів регресії (SSR) – сума квадратів різниць між прогнозованими точками даних (ŷ i ) і середнім значенням змінної відповіді ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Помилка суми квадратів (SSE) – сума квадратів різниць між прогнозованими точками даних (ŷ i ) і спостережуваними точками даних (y i ).
- SSE = Σ(ŷ i – y i ) 2
У наведеному нижче покроковому прикладі показано, як обчислити кожен із цих показників для даної моделі регресії в Excel.
Крок 1: Створіть дані
По-перше, давайте створимо набір даних, який містить кількість вивчених годин і результати іспитів, отримані для 20 різних студентів у певній школі:
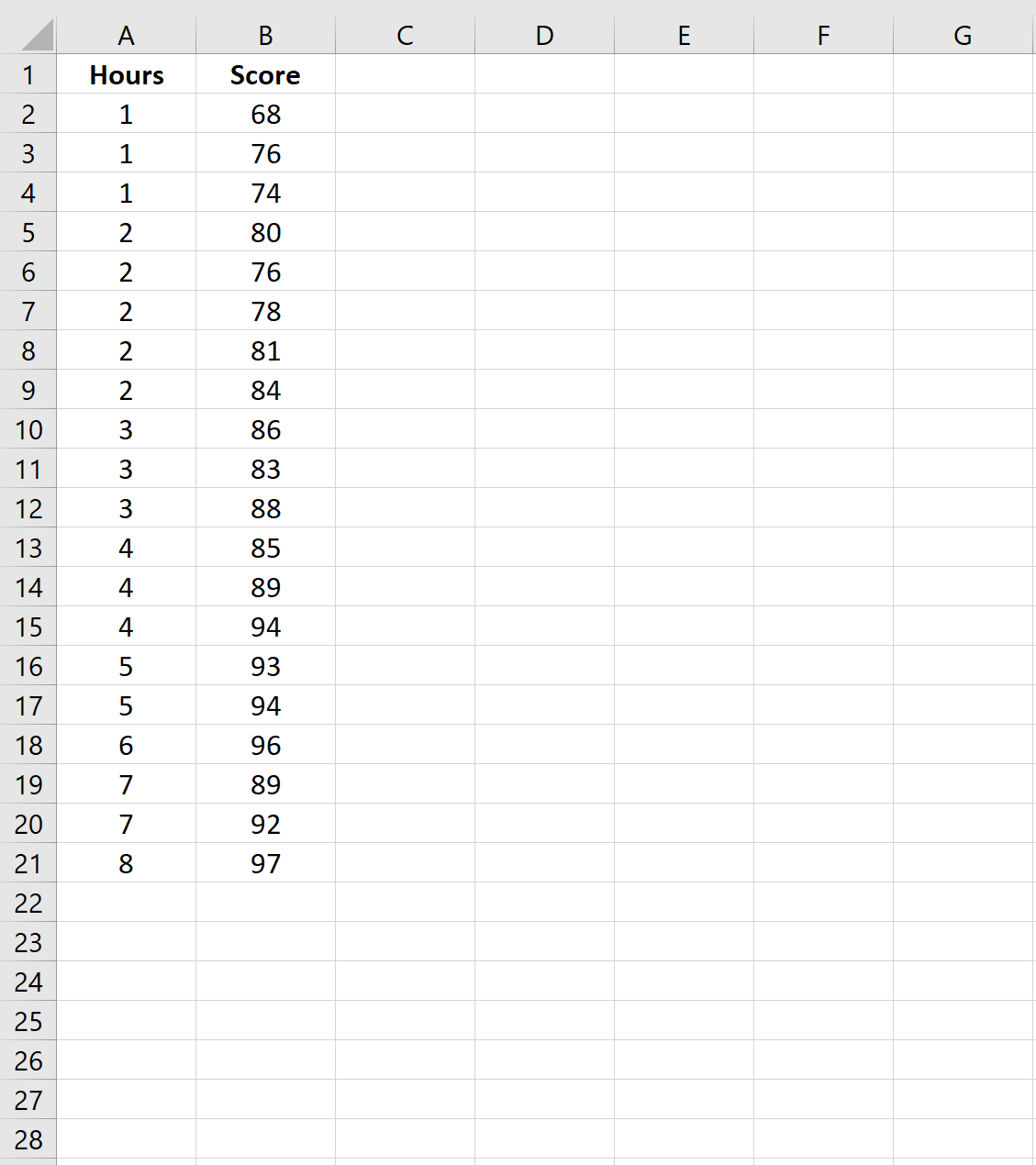
Крок 2. Підберіть регресійну модель
На верхній стрічці Excel клацніть вкладку Дані та натисніть Аналіз даних . Якщо ви не бачите цей параметр, спершу потрібно інсталювати безкоштовне програмне забезпечення Analysis ToolPak .
Коли ви натиснете «Аналіз даних», з’явиться нове вікно. Виберіть «Регресія» та натисніть «ОК».
У новому вікні, що з’явиться, введіть таку інформацію:
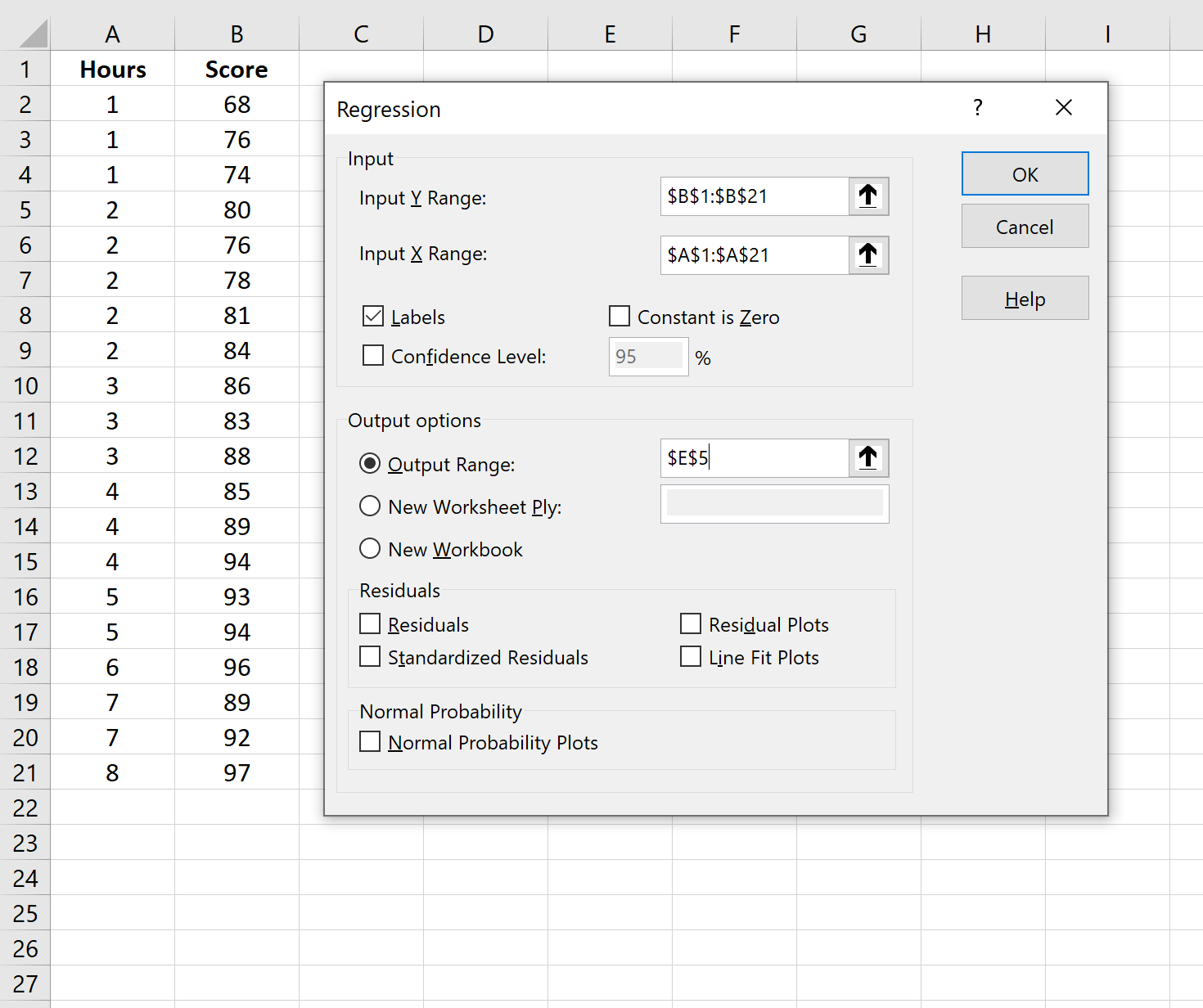
Після натискання кнопки OK з’явиться результат регресії.
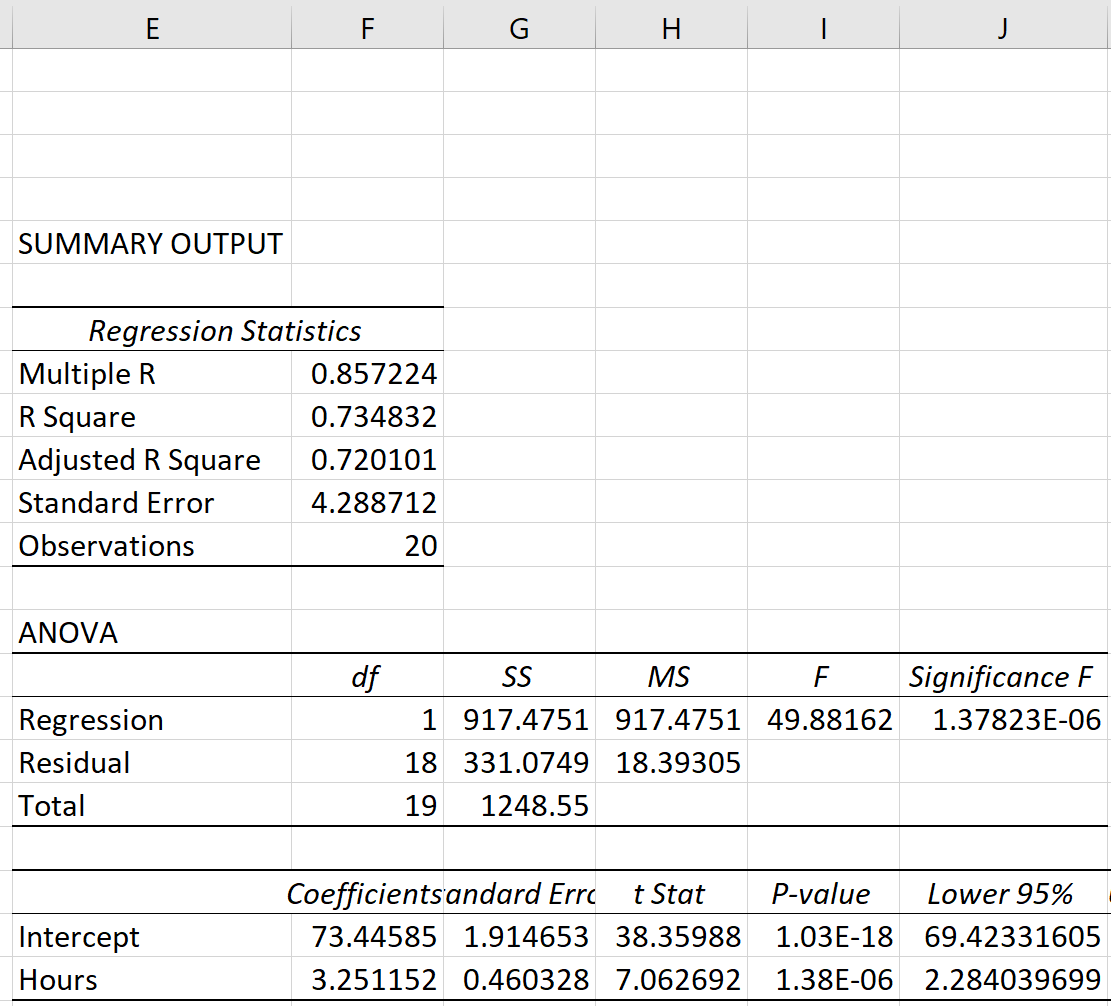
Крок 3: Проаналізуйте результат
Три показники суми квадратів – SST, SSR і SSE – можна побачити в стовпці SS таблиці ANOVA :
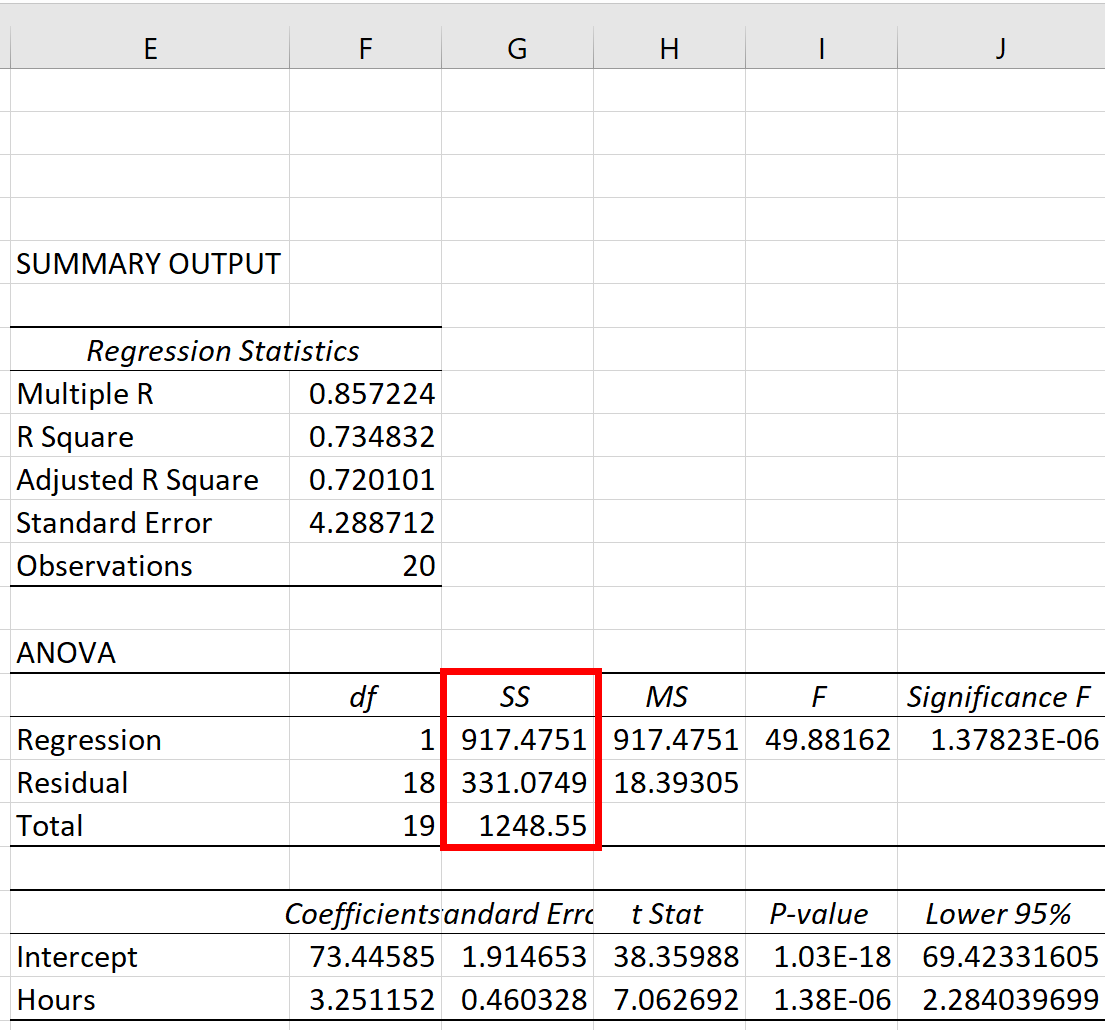
Показники виявляються такими:
- Загальна сума квадратів (SST): 1248.55
- Сума квадратів регресії (SSR): 917,4751
- Похибка суми квадратів (SSE): 331,0749
Ми можемо перевірити, що SST = SSR + SSE:
- SST = SSR + SSE
- 1248,55 = 917,4751 + 331,0749
Ми також можемо вручну обчислити R у квадраті регресійної моделі:
- R у квадраті = SSR / SST
- R у квадраті = 917,4751 / 1248,55
- R у квадраті = 0,7348
Це говорить нам про те, що 73,48% варіації оцінок на іспитах можна пояснити кількістю вивчених годин.
Додаткові ресурси
Як виконати просту лінійну регресію в Excel
Як виконати множинну лінійну регресію в Excel
Як виконати поліноміальну регресію в Excel
Як виконати експоненціальну регресію в Excel
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше