Як виконати кореляційний t-тест

Коефіцієнт кореляції Пірсона використовується для кількісного визначення лінійного зв’язку між двома змінними.

Він завжди приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію.
• 0 означає відсутність лінійної кореляції.
• 1 вказує на абсолютно позитивну лінійну кореляцію.

Щоб визначити, чи є коефіцієнт кореляції статистично значущим, ви можете виконати t-тест, який передбачає обчислення t-показника та відповідного p-значення.

Формула для розрахунку t-показника така:

t = r√ (n-2) / (1-r ² )

золото:

• r: Коефіцієнт кореляції
• n: розмір вибірки

P-значення обчислюється як відповідне двостороннє p-значення для t-розподілу з n-2 ступенями свободи.

У наступному прикладі показано, як виконати t-тест для коефіцієнта кореляції.

Приклад: виконання t-тесту для кореляції

Припустимо, ми маємо наступний набір даних із двома змінними:

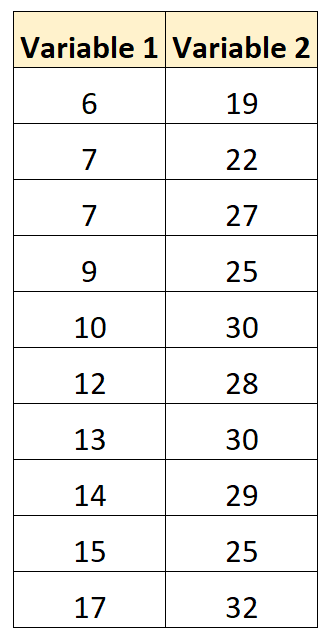
Використовуючи деяке статистичне програмне забезпечення (Excel, R, Python тощо), ми можемо обчислити коефіцієнт кореляції між двома змінними, який становить 0,707 .

Це дуже позитивна кореляція, але щоб визначити, чи є вона статистично значущою, нам потрібно обчислити відповідний t-показник і p-значення.

Ми можемо розрахувати t-показник наступним чином:

• t = r√ (n-2) / (1-r ² )
• t = 0,707√ (10-2) / (1-0,707 ² )
• t = 2,828

Використовуючи калькулятор T-балів P-value , ми знаходимо, що відповідне p-value дорівнює 0,022 .

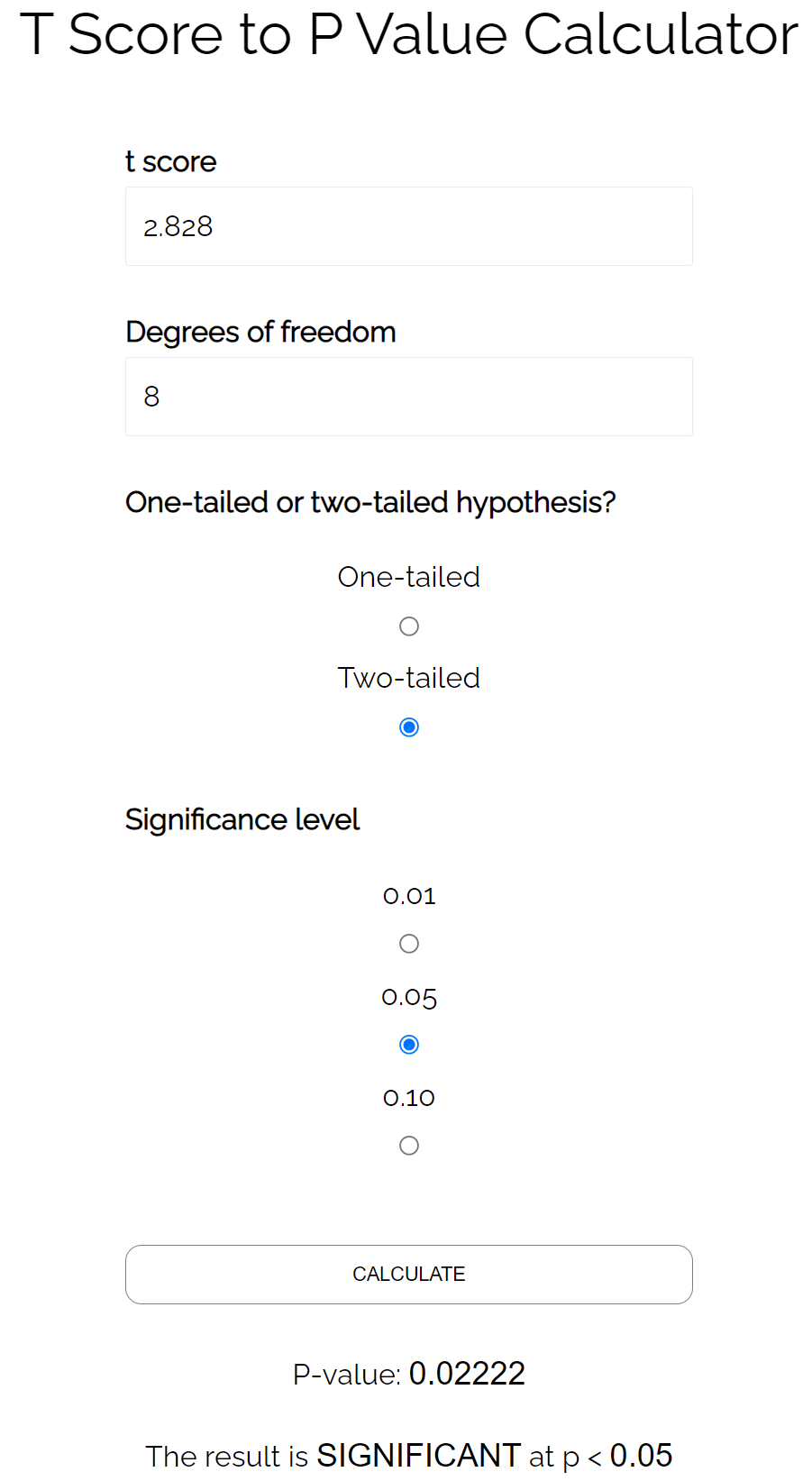
Оскільки це p-значення менше 0,05, можна зробити висновок, що кореляція між цими двома змінними є статистично значущою.

Додаткові ресурси

Як виконати кореляційний тест в Excel
Як виконати кореляційний тест у R
Що вважається «слабкою» кореляцією?
Що вважається «сильною» кореляцією?