T-score проти z-score: коли їх використовувати?

Два терміни, які часто плутають студентів на курсах статистики, це t-показники та z-показники .

Обидва широко використовуються під час перевірки гіпотез або побудови довірчих інтервалів , але вони дещо відрізняються.

Ось формула для кожного:

оцінка t = ( x – μ) / (s/√ n )

золото:

• x : вибірка середніх
• μ : середня чисельність населення
• s : Стандартне відхилення вибірки
• n : розмір вибірки

z-оцінка = ( x – μ) / σ

золото:

• x : значення необроблених даних
• μ : середня чисельність населення
• σ : стандартне відхилення сукупності

Ця блок-схема показує, коли вам слід використовувати кожен із них на основі ваших даних:

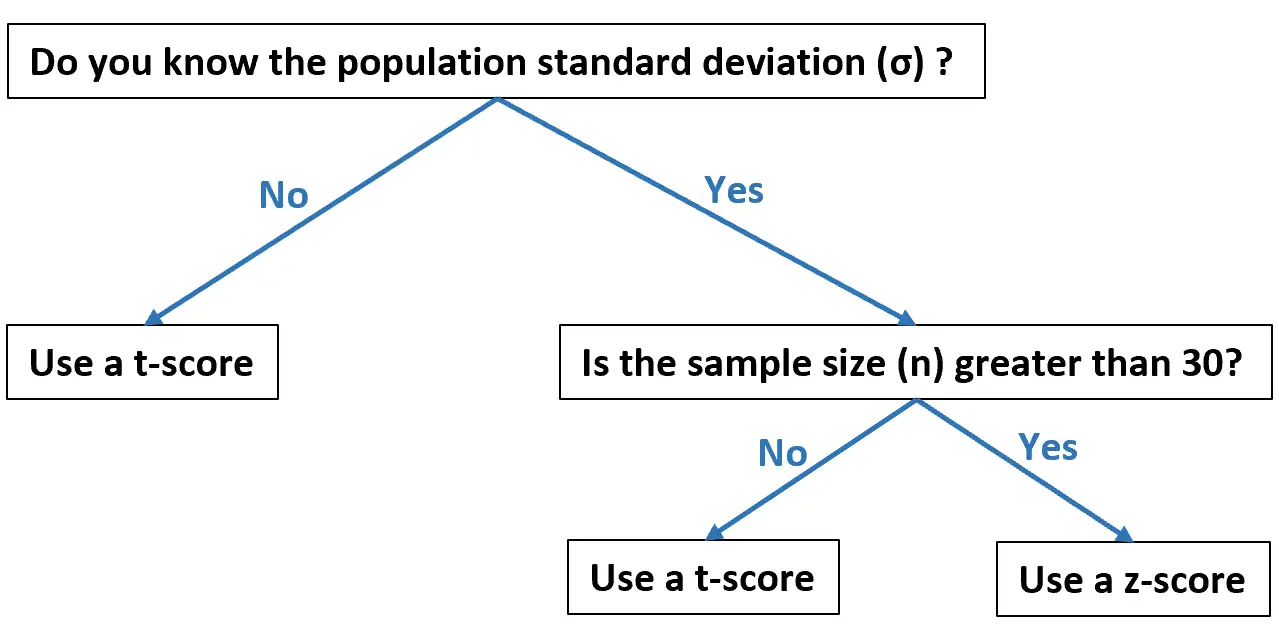
У наведених нижче прикладах показано, як на практиці розрахувати T-показник і Z-показник.

Приклад 1: Розрахунок Т-показника

Припустімо, що ресторан готує гамбургери, стверджуючи, що вони мають середню вагу μ = 0,25 фунта.

Припустимо, ми беремо випадкову вибірку з n = 20 гамбургерів і знаходимо, що середня вага вибірки становить x = 0,22 фунта зі стандартним відхиленням s = 0,05 фунта. Виконайте перевірку гіпотези, щоб визначити, чи дорівнює фактична середня вага всіх гамбургерів, вироблених у цьому ресторані, 0,25 фунта.

У цьому прикладі ми використаємо Т-оцінку для перевірки гіпотези, оскільки жодна з наступних двох умов не виконується.

• Стандартне відхилення сукупності (σ) відоме. (у цьому прикладі σ не вказано)
• Розмір вибірки перевищує 30. (n=20 у цьому прикладі)

Отже, ми розрахуємо t-показник наступним чином:

• оцінка t = ( x – μ) / (s/√ n )
• t-показник = (0,22 – 0,25) / (0,05 / √ 20 )
• t-показник = -2,68

Відповідно до калькулятора T-показника P-value , значення p, яке відповідає цьому t-показнику, становить 0,01481 .

Оскільки це p-значення менше 0,05, у нас є достатньо доказів, щоб стверджувати, що середня вага гамбургерів, вироблених у цьому ресторані, не дорівнює 0,25 фунта.

Приклад 2: Розрахунок балу Z

Припустимо, що компанія виробляє батареї, термін служби яких, як відомо, відповідає нормальному розподілу із середнім значенням μ = 20 годин і стандартним відхиленням σ = 5 годин.

Припустимо, ми беремо випадкову вибірку з n = 50 батарей і знаходимо, що середнє значення вибірки становить x = 21 година. Виконайте перевірку гіпотези, щоб визначити, чи справжній середній термін служби всіх батарей, вироблених цією компанією, дорівнює 20 годинам.

У цьому прикладі ми використаємо z-показник для перевірки гіпотези, оскільки виконуються обидві наступні умови:

• Стандартне відхилення сукупності (σ) відоме. (у цьому прикладі σ дорівнює 5)
• Розмір вибірки перевищує 30. (n=50 у цьому прикладі)

Отже, ми обчислюємо z-оцінку наступним чином:

• z-оцінка = ( x – μ) / σ
• z-оцінка = (21 – 20) / 5
• z-оцінка = 0,2

Згідно з калькулятором Z-показника P-значення, значення p, яке відповідає цьому z-показнику, становить 0,84184 .

Оскільки це значення p не менше 0,05, ми не маємо достатніх доказів того, що середній термін служби всіх батарей, вироблених цією компанією, відрізняється від 20 годин.

Додаткові ресурси

Наступні навчальні посібники пропонують більше інформації про бали T і Z:

Нормальний розподіл проти розподілу t: у чому різниця?
Як читати таблицю розподілу t
Як читати таблицю Z