Розуміння t-тесту в лінійній регресії

Лінійна регресія використовується для кількісного визначення зв’язку між змінною прогностикою та змінною відповіді.

Щоразу, коли ми виконуємо лінійну регресію, ми хочемо знати, чи існує статистично значущий зв’язок між змінною предиктора та змінною відповіді.

Ми перевіряємо значущість, виконуючи t-тест для нахилу регресії. Ми використовуємо таку нульову та альтернативну гіпотезу для цього t-критерію:

• H ₀ : β ₁ = 0 (нахил дорівнює нулю)
• H _A : β ₁ ≠ 0 (нахил не дорівнює нулю)

Потім ми обчислюємо тестову статистику наступним чином:

t = b / SE _b

золото:

• b : оцінка коефіцієнта
• SE _b : стандартна помилка оцінки коефіцієнта

Якщо p-значення, яке відповідає t , нижче певного порогу (наприклад, α = 0,05), тоді ми відхиляємо нульову гіпотезу та робимо висновок, що існує статистично значущий зв’язок між змінною предиктора та змінною відповіді.

У наступному прикладі показано, як на практиці виконати t-тест для моделі лінійної регресії.

Приклад: виконання t-тесту для лінійної регресії

Припустімо, професор хоче проаналізувати співвідношення між вивченими годинами та оцінками іспиту для 40 своїх студентів.

Він виконує просту лінійну регресію, використовуючи вивчені години як змінну прогностику та оцінки за іспит як змінну відповіді.

У наведеній нижче таблиці показано результати регресійної моделі:

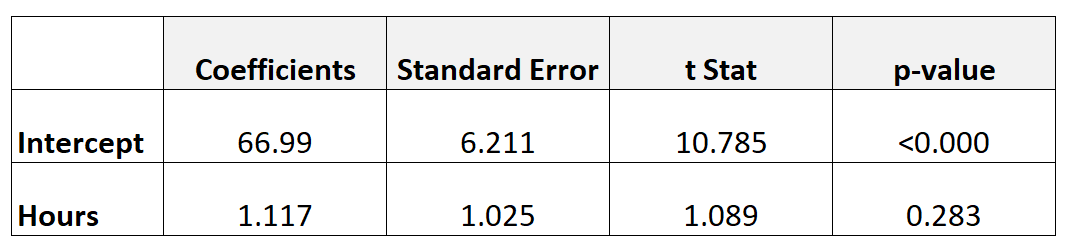
Щоб визначити, чи вивчені години мають статистично значущий зв’язок з оцінкою підсумкового іспиту, ми можемо виконати t-тест.

Ми використовуємо таку нульову та альтернативну гіпотезу для цього t-критерію:

• H ₀ : β ₁ = 0 (нахил досліджуваних годин дорівнює нулю)
• H _A : β ₁ ≠ 0 (нахил досліджуваних годин не дорівнює нулю)

Потім ми обчислюємо тестову статистику наступним чином:

• t = b / SE _b
• t = 1,117 / 1,025
• t = 1,089

P-значення, яке відповідає t = 1,089 з df = n-2 = 40 – 2 = 38, становить 0,283 .

Зауважте, що для обчислення цього значення p ми також можемо використовувати калькулятор відношення показника T до P :

Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу.

Це означає, що вивчені години не мають статистично значущого зв’язку між результатами фінального іспиту.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про лінійну регресію.

Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
Як інтерпретувати коефіцієнти регресії
Як інтерпретувати тест F для загальної значущості в регресії