Як виконувати t-тести в google таблицях

Загалом, існує три типи t-тестів:

• Зразок t тесту
• Двовибірковий Т-тест
• Т-критерій парних вибірок

У цьому посібнику наведено приклади виконання кожного з цих тестів у Google Таблицях.

Приклад: одновибірковий t-тест

Визначення: одновибірковий t-критерій використовується, щоб перевірити, чи дорівнює середнє значення генеральної сукупності певному значенню.

Приклад: ботанік хоче знати, чи дорівнює середня висота певного виду рослин 15 дюймам. Вона бере випадкову вибірку з 12 рослин і записує кожну їх висоту в дюймах.

На наступному знімку екрана показано, як виконати t-тест для однієї вибірки, щоб визначити, чи дорівнює справжній середній зріст населення 15 дюймам:

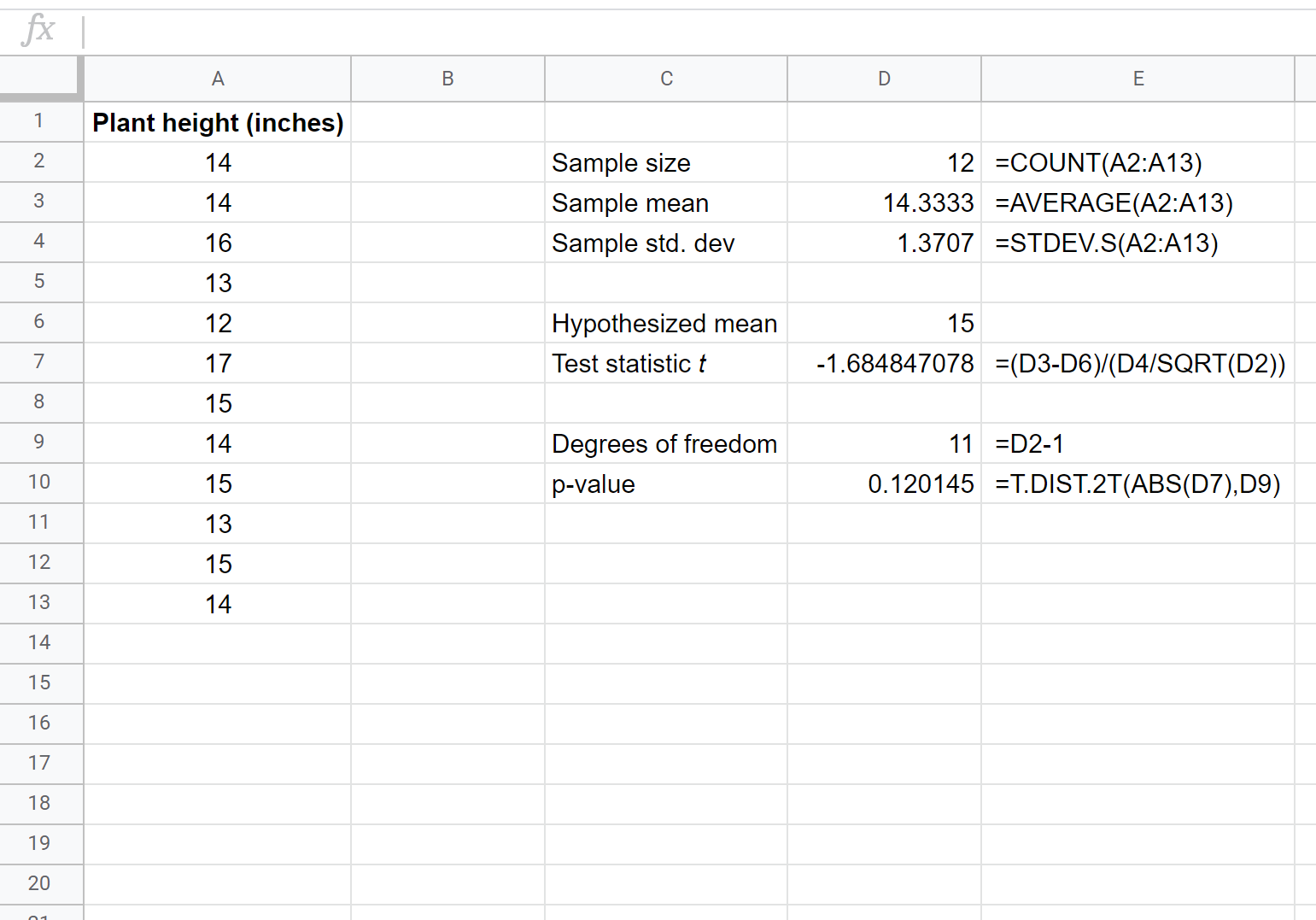
Дві гіпотези для цього t-критерію на певній вибірці такі:

H ₀ : µ = 15 (середня висота цього виду рослин 15 дюймів)

H _A : µ ≠15 (середній зріст не становить 15 дюймів)

P-значення нашого тесту (0,120145) більше, ніж альфа = 0,05, ми не можемо відхилити нульову гіпотезу тесту. У нас немає достатніх доказів, щоб стверджувати, що середня висота цього конкретного виду рослин є чимось іншим, ніж 15 дюймів.

Приклад: двовибірковий t-тест

Визначення: двовибірковий t-критерій використовується, щоб перевірити, чи рівні середні дві сукупності чи ні.

Приклад: дослідники хочуть знати, чи мають два різні види рослин у певній країні однакову середню висоту. Вони збирають випадкову вибірку з 20 рослин кожного виду та записують висоту кожної рослини в дюймах.

На наступному знімку екрана показано, як виконати t-тест із двома вибірками за допомогою функції T.TEST() , щоб визначити, чи є середні зрости двох популяцій рівними:

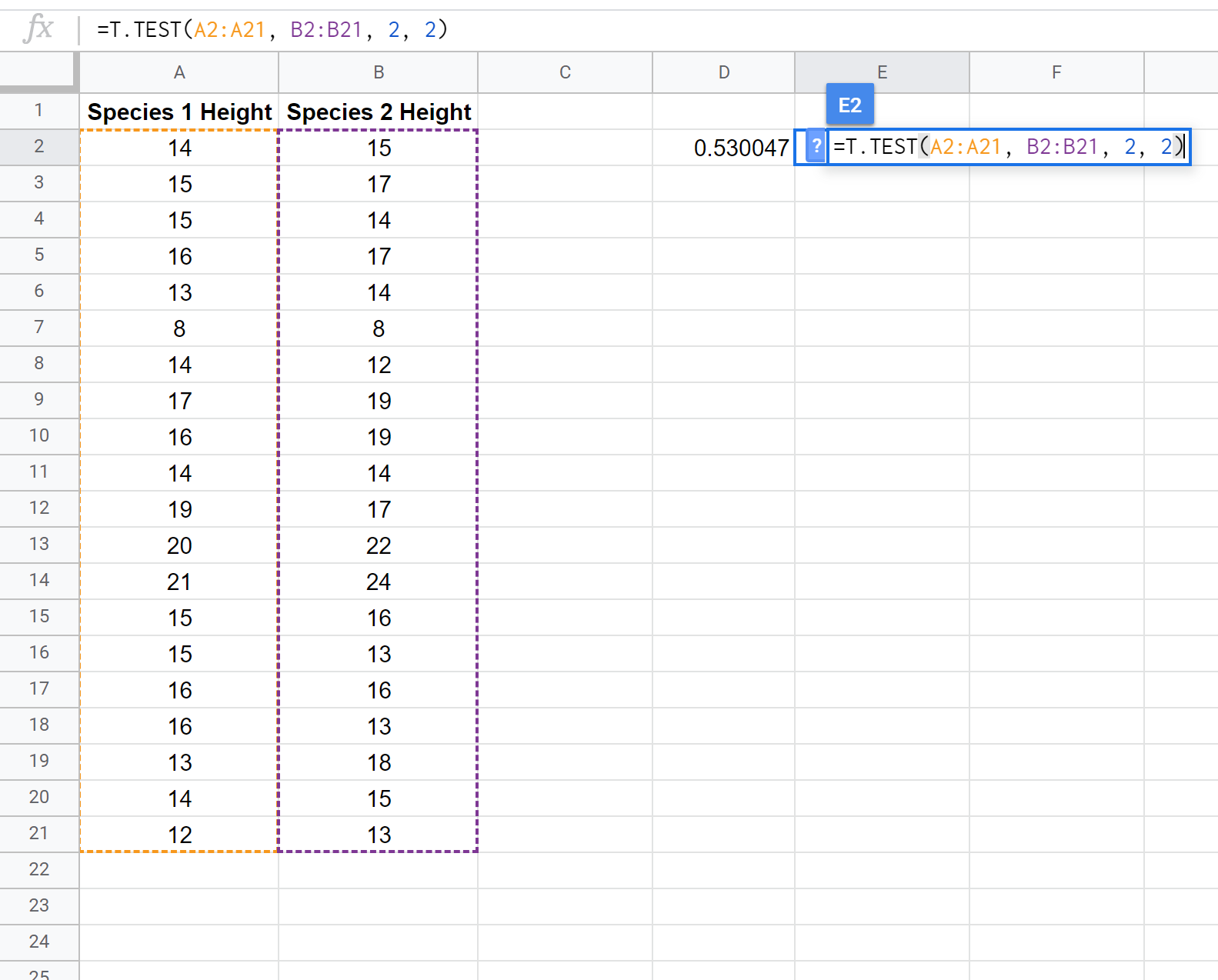
Примітка: також можна виконати однобічний двовибірковий t-критерій з або без припущення, що дві вибірки мають однакову дисперсію. Зверніться до документації T.TEST , щоб дізнатися, як налаштувати припущення тесту.

Дві гіпотези для цього двовибіркового t-критерію:

H ₀ : μ ₁ = μ ₂ (два середні сукупності рівні)

H ₁ : μ ₁ ≠ μ ₂ (два середні сукупності не рівні)

Оскільки p-значення нашого тесту (0,530047) більше, ніж альфа = 0,05, ми не можемо відхилити нульову гіпотезу тесту. У нас немає достатніх доказів, щоб стверджувати, що середня висота цього конкретного виду рослин є чимось іншим, ніж 15 дюймів.

Приклад: t-критерій парних зразків

Визначення: t-критерій парних вибірок використовується для порівняння середніх значень двох вибірок, коли кожне спостереження з однієї вибірки можна пов’язати зі спостереженням з іншої вибірки.

Приклад: ми хочемо знати, чи курс навчання має значний вплив на успішність студентів на конкретному іспиті. Щоб перевірити це, ми просимо 20 учнів у класі пройти попередній тест. Тоді ми маємо кожного зі студентів брати участь у навчальній програмі протягом двох тижнів. Потім студенти повторно складають тест подібної складності.

На наступному знімку екрана показано, як виконати t-критерій парної вибірки, щоб порівняти різницю між середніми значеннями першого та другого тестів:

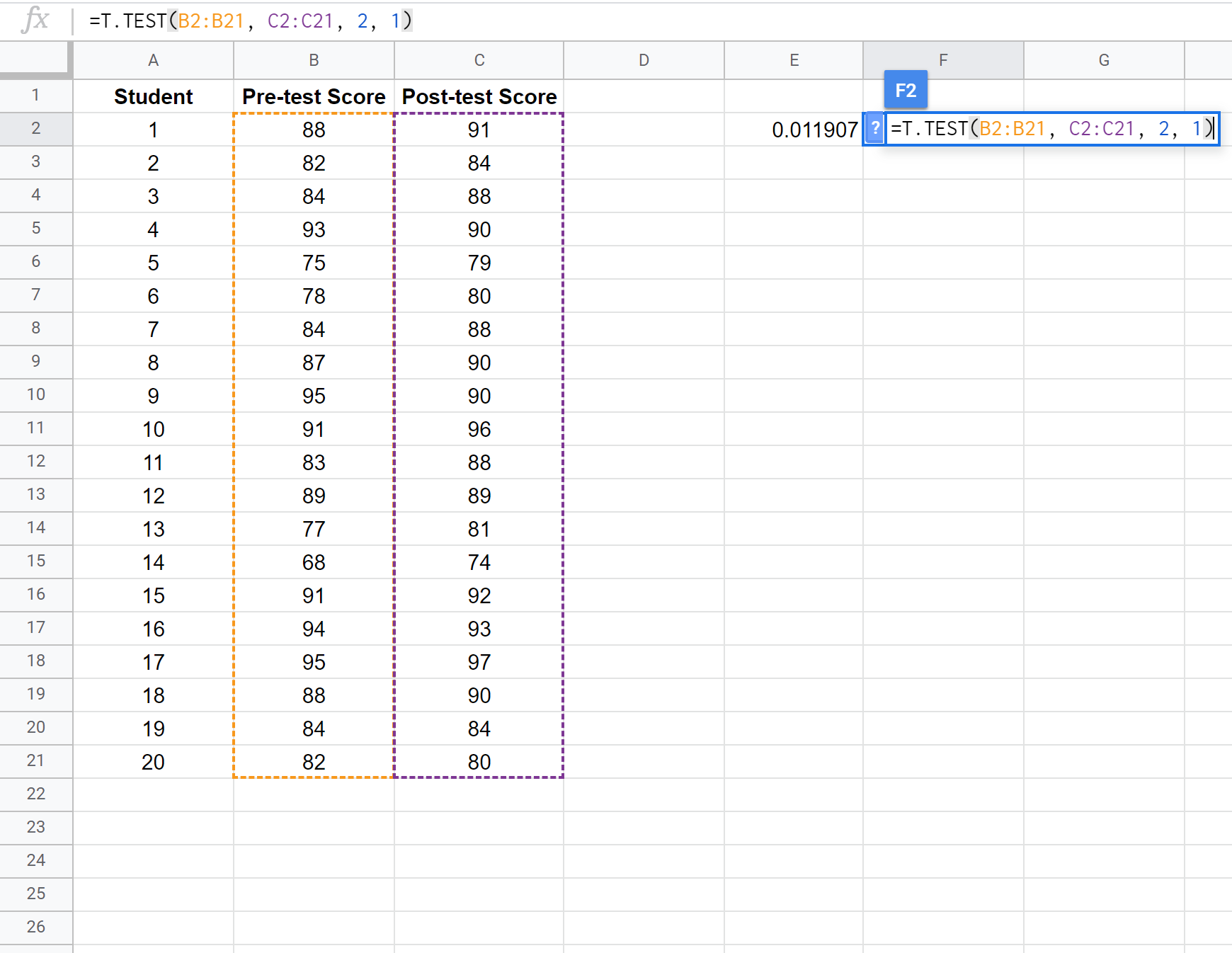
Примітка: також можна виконати однобічний двовибірковий t-критерій з або без припущення, що дві вибірки мають однакову дисперсію. Зверніться до документації T.TEST , щоб дізнатися, як налаштувати припущення тесту.

Два припущення для цього t-критерію парних зразків:

H ₀ : μ ₁ = μ ₂ (два середні сукупності рівні)

H ₁ : μ ₁ ≠ μ ₂ (два середні сукупності не рівні)

Оскільки p-значення нашого тесту (0,011907) менше, ніж альфа = 0,05, ми відхиляємо нульову гіпотезу тесту. У нас є достатньо доказів, щоб стверджувати, що існує статистично значуща різниця між середнім балом до і після тесту.