Як виконати пост-тест тьюкі-крамера в excel

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

У дисперсійному аналізі використовуються такі припущення :

Нульова гіпотеза (H ₀ ): µ ₁ = µ ₂ = µ ₃ = … = µ _k (середні рівні для кожної групи)

Альтернативна гіпотеза: (Ha): принаймні одне із середніх відрізняється від інших

Якщо p-значення ANOVA нижче рівня значущості, ми можемо відхилити нульову гіпотезу та зробити висновок, що у нас є достатньо доказів, щоб стверджувати, що принаймні одне з групових середніх відрізняється від інших.

Однак це не говорить нам , які групи відрізняються одна від одної. Це просто говорить нам про те, що не всі середні групові показники однакові. Для того, щоб точно знати, які групи відрізняються одна від одної, нам потрібно провести ретельний тест.

Найпоширенішим тестом post hoc є тест Тьюкі-Крамера , який порівнює середнє значення між кожною попарною комбінацією груп.

У наведеному нижче прикладі показано, як виконати тест Тьюкі-Крамера в Excel.

Приклад: тест Тьюкі-Крамера в Excel

Припустімо, ми виконуємо односторонній ANOVA для трьох груп: A, B і C. Результати одностороннього ANOVA наведені нижче:

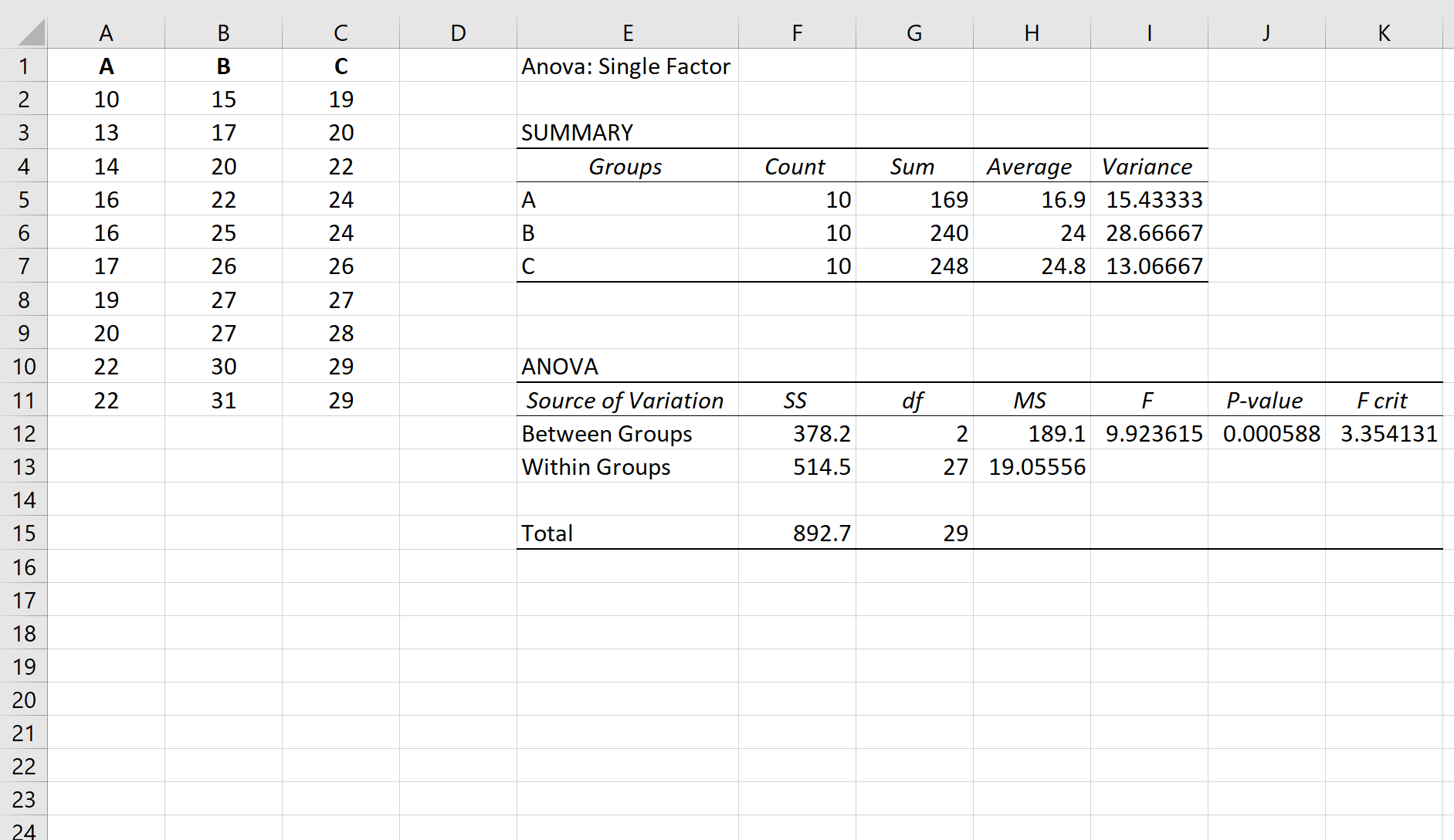
Пов’язане: Як виконати односторонній дисперсійний аналіз у Excel

P-значення таблиці ANOVA становить 0,000588 . Оскільки це p-значення менше 0,05, ми можемо відхилити нульову гіпотезу та зробити висновок, що середні значення між трьома групами не рівні.

Щоб точно визначити , які групові середні відрізняються, ми можемо виконати тест Tukey-Kramer post hoc, використовуючи такі кроки:

Крок 1: Знайдіть абсолютну середню різницю між кожною групою.

Спочатку ми знайдемо абсолютну середню різницю між кожною групою, використовуючи середні значення, наведені в першій таблиці результату ANOVA:

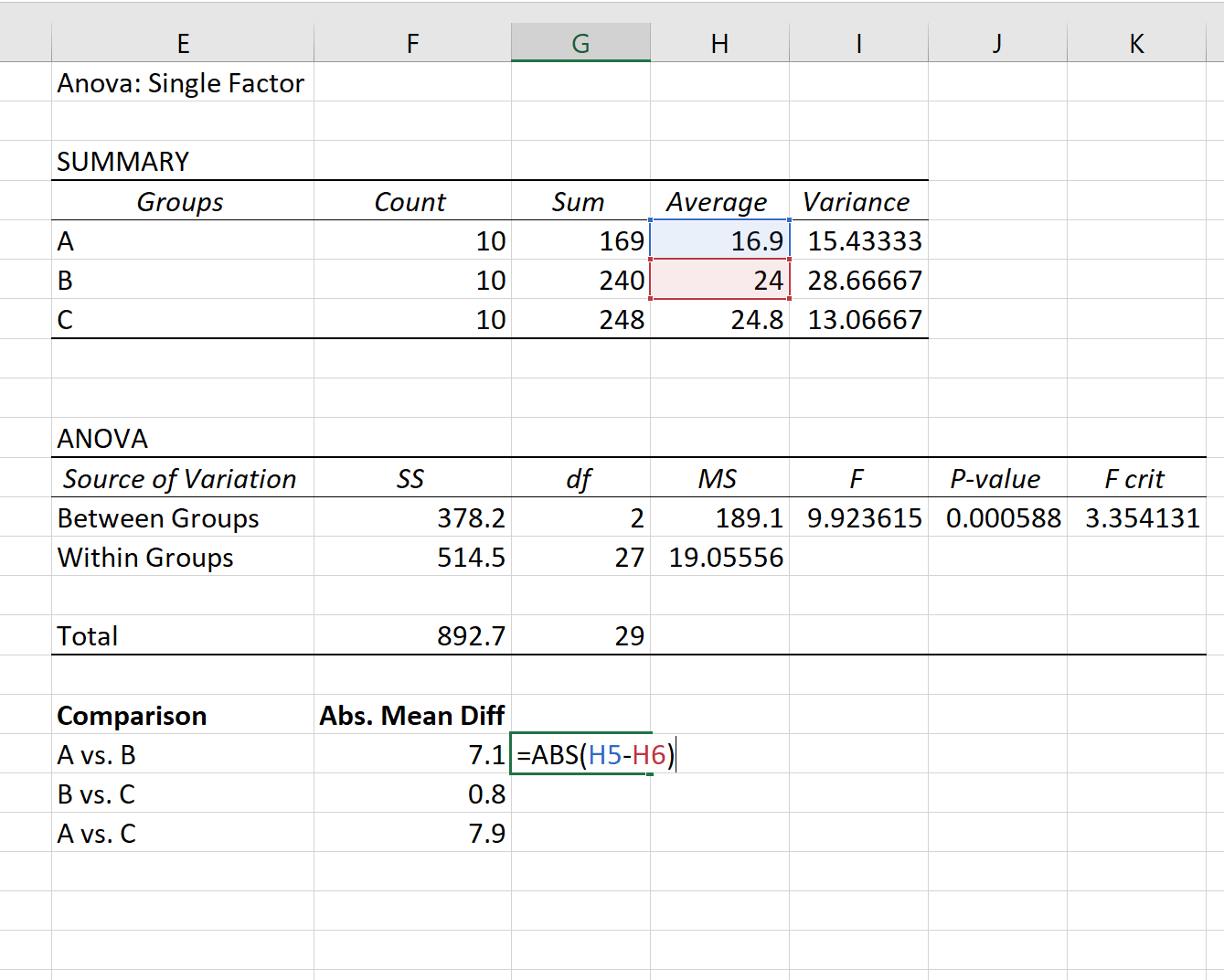
Крок 2: Знайдіть критичне значення Q.

Далі нам потрібно знайти критичне значення Q за такою формулою:

Критичне значення Q = Q*√(s ² _{згруповані} / n.)

золото:

• Q = значення діапазону таблиці студента Q
• s ² _{об’єднані} = дисперсія об’єднана по всіх групах
• ні. = Розмір вибірки для даної групи

Щоб знайти значення Q, ви можете звернутися до таблиці Q діапазону Studentized, яка виглядає так:

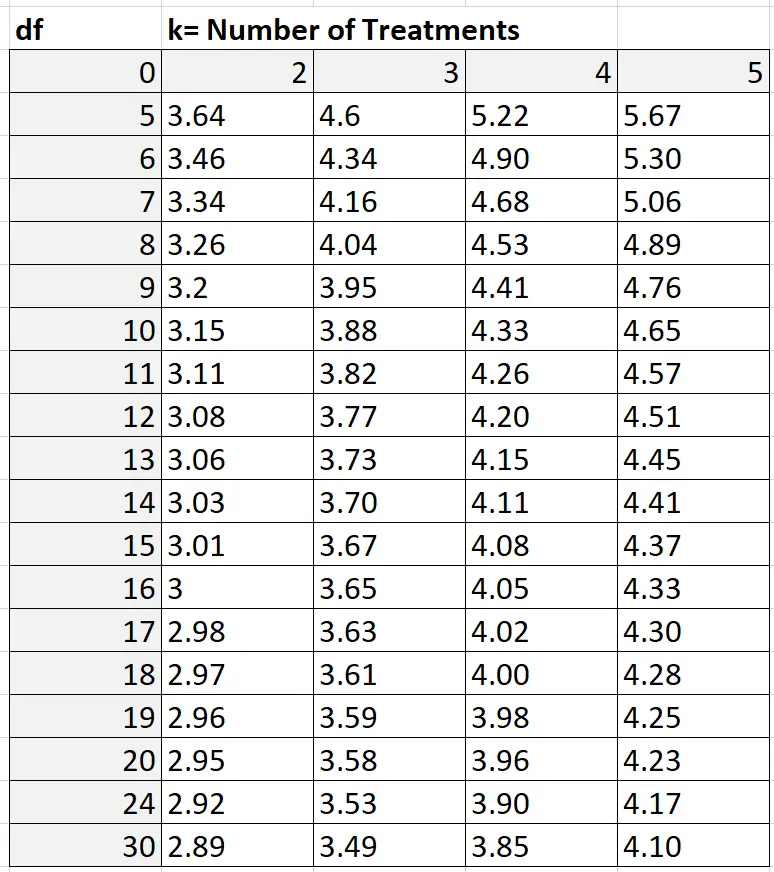
У нашому прикладі k = кількість груп, тобто k = 3. Ступені свободи обчислюються як: nk = 30 – 3 = 27. Оскільки 27 не показано в таблиці вище, ми можемо використовувати консервативну оцінку 24 Виходячи з k = 3 і df = 24, ми знаходимо, що Q = 3,53 .

Об’єднану дисперсію можна розрахувати як середнє значення дисперсій груп, яке виявляється рівним 19,056 .

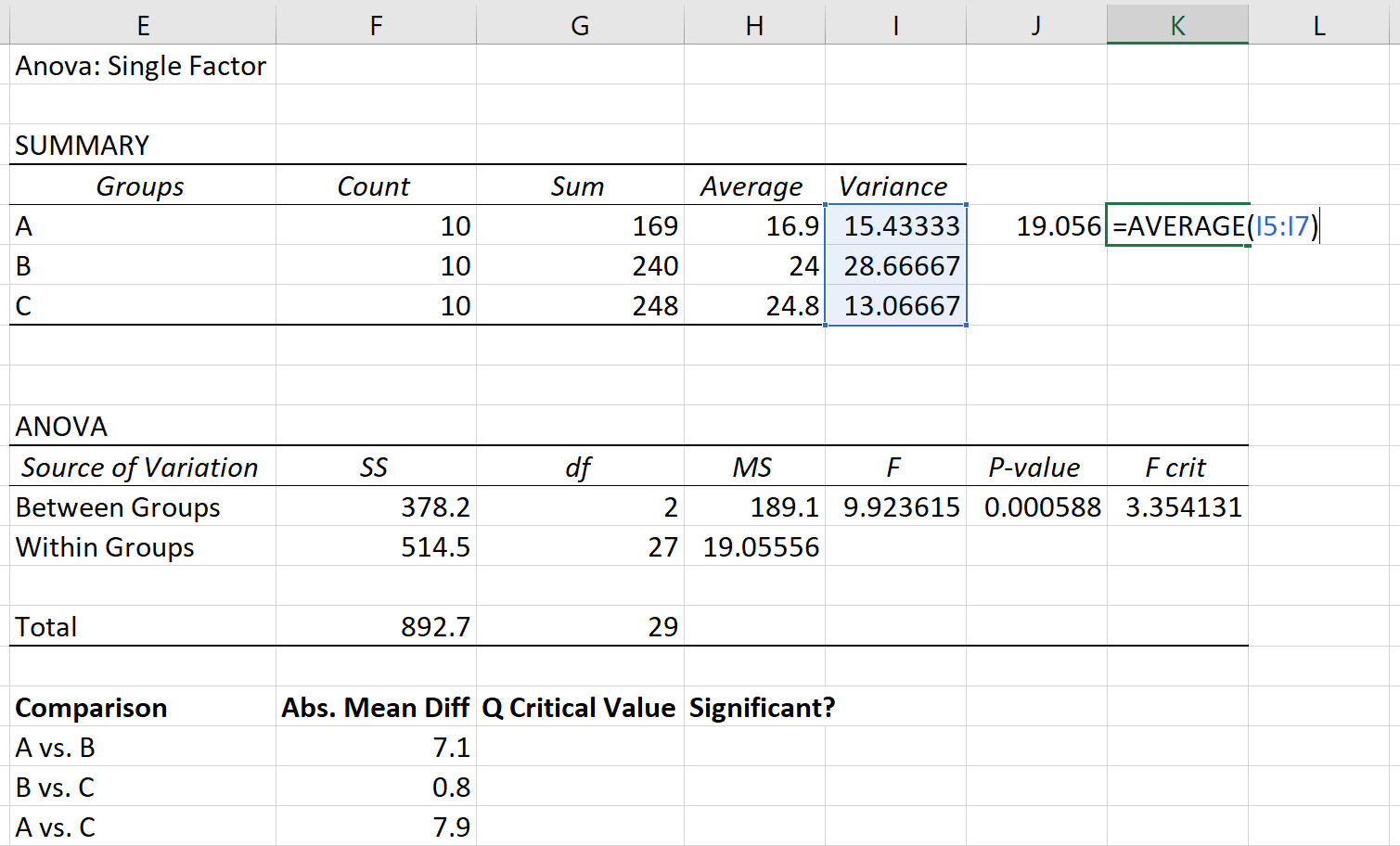
Нарешті, розмір вибірки кожної групи становить 10.

Таким чином, наше критичне значення Q можна обчислити таким чином:

Критичне значення Q = Q*√(s ² _{згруповані} / n.) = 3,53*√(19,056/10) = 4,87 .

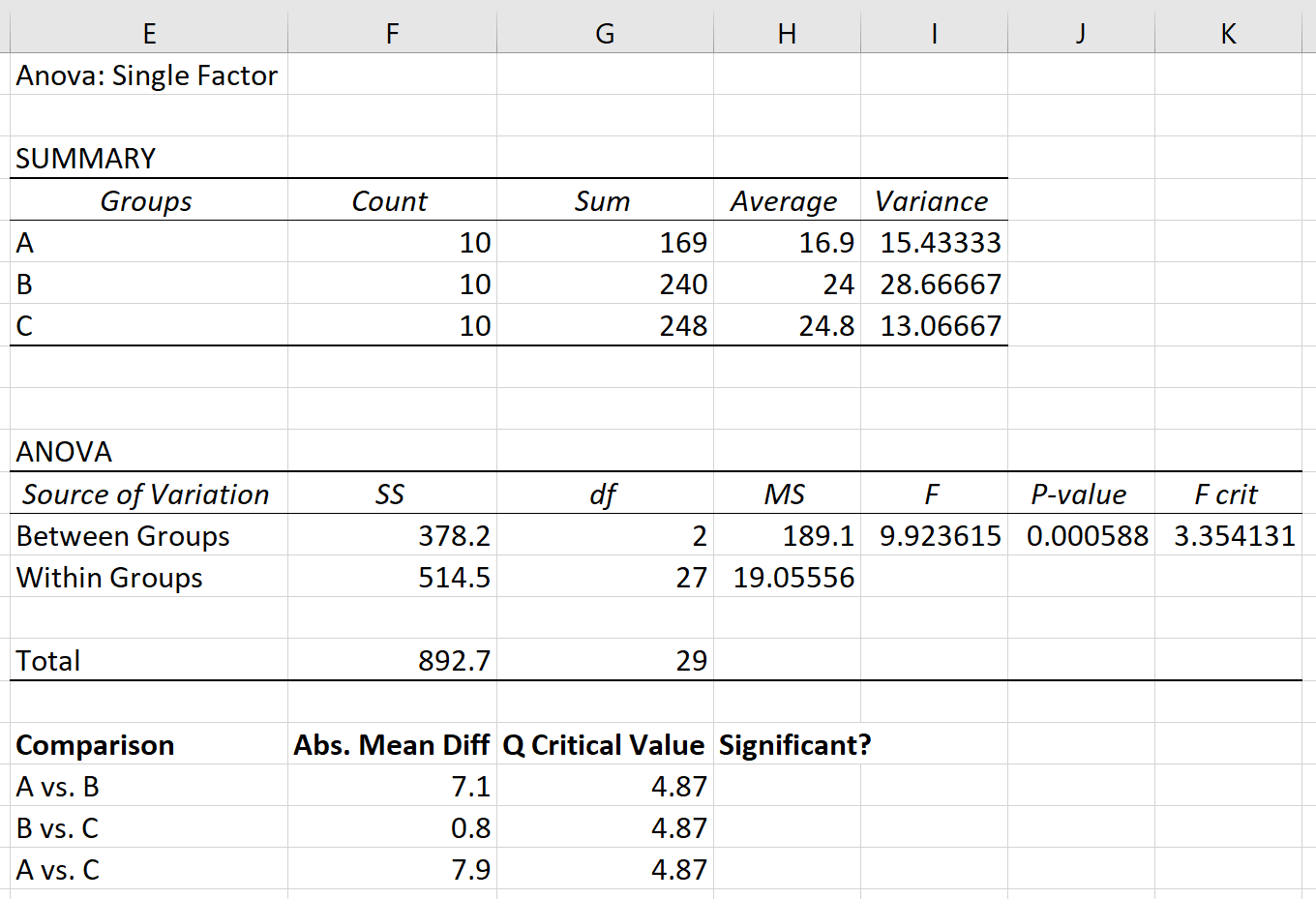
Крок 3: Визначте, які середні групи відрізняються .

Нарешті, ми можемо порівняти абсолютну середню різницю між кожною групою з критичним значенням Q. Якщо абсолютна середня різниця більша за критичне значення Q, тоді різниця між груповими середніми є статистично значущою:

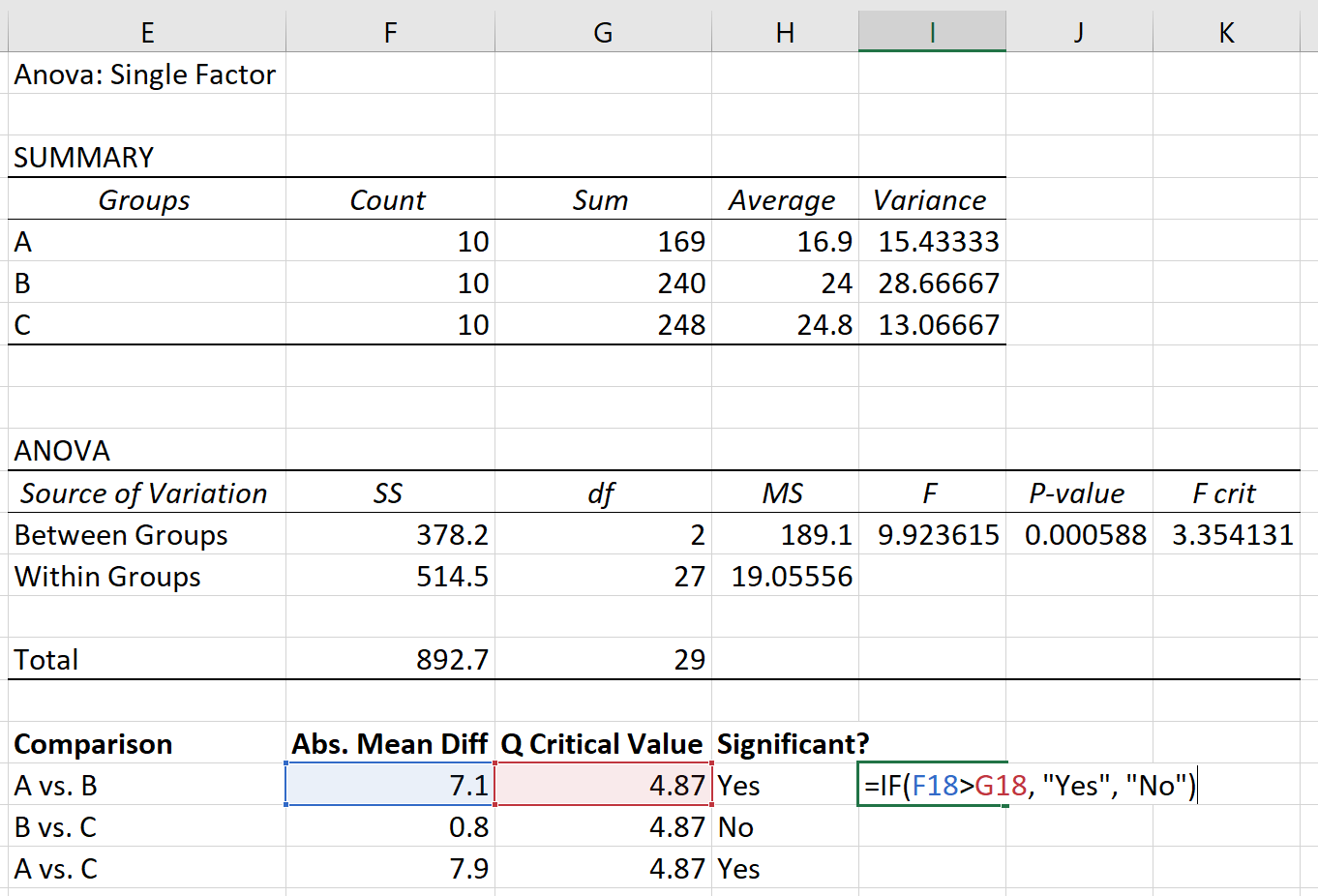
На основі тесту Tukey-Kramer post hoc ми виявили наступне:

• Різниця в середніх значеннях між групою А та групою В є статистично значущою.
• Різниця в середніх значеннях між групою B і групою C не є статистично значущою.
• Різниця в середніх значеннях між групою А та групою С є статистично значущою.

Додаткові ресурси

Як виконати односторонній дисперсійний аналіз в Excel
Посібник із використання пост-хок тестування з ANOVA