Як розрахувати z-оцінки в google таблицях

У статистиці z-показник говорить нам, скільки стандартних відхилень має значення від середнього . Ми використовуємо наступну формулу для розрахунку z-показника:

z = (X – μ) / σ

золото:

• X – це одне значення необроблених даних
• μ — середнє значення набору даних
• σ — стандартне відхилення набору даних

У цьому підручнику пояснюється, як обчислити z-показники для необроблених значень даних у Google Таблицях.

Приклад: z-оцінки в Google Таблицях

Припустімо, що ми маємо такий набір даних і хочемо знайти z-показник для кожного значення вихідних даних:

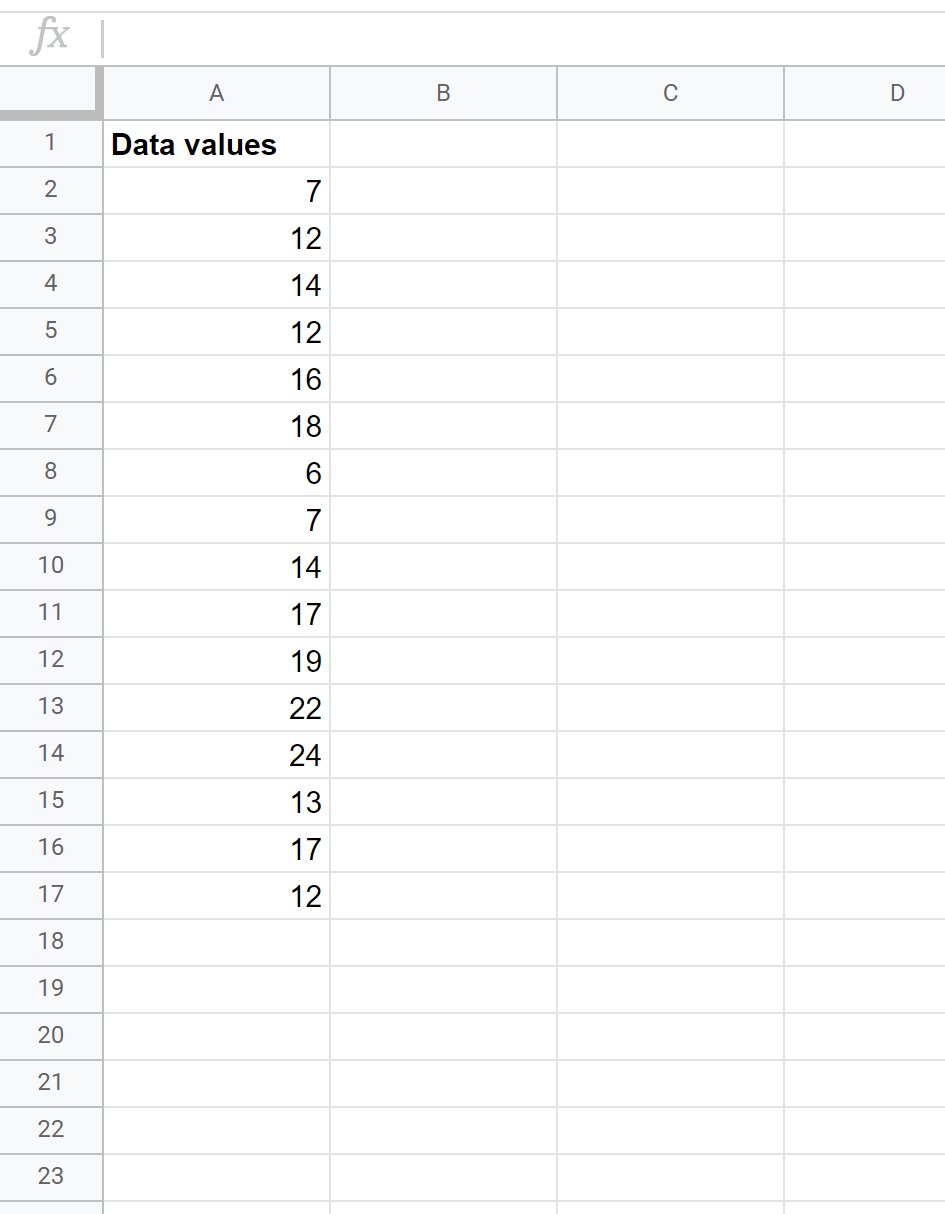
Для цього ми можемо виконати наступні кроки.

Крок 1: Знайдіть середнє значення та стандартне відхилення набору даних.

По-перше, нам потрібно знайти середнє значення та стандартне відхилення набору даних. Наступні формули показують, як це зробити:

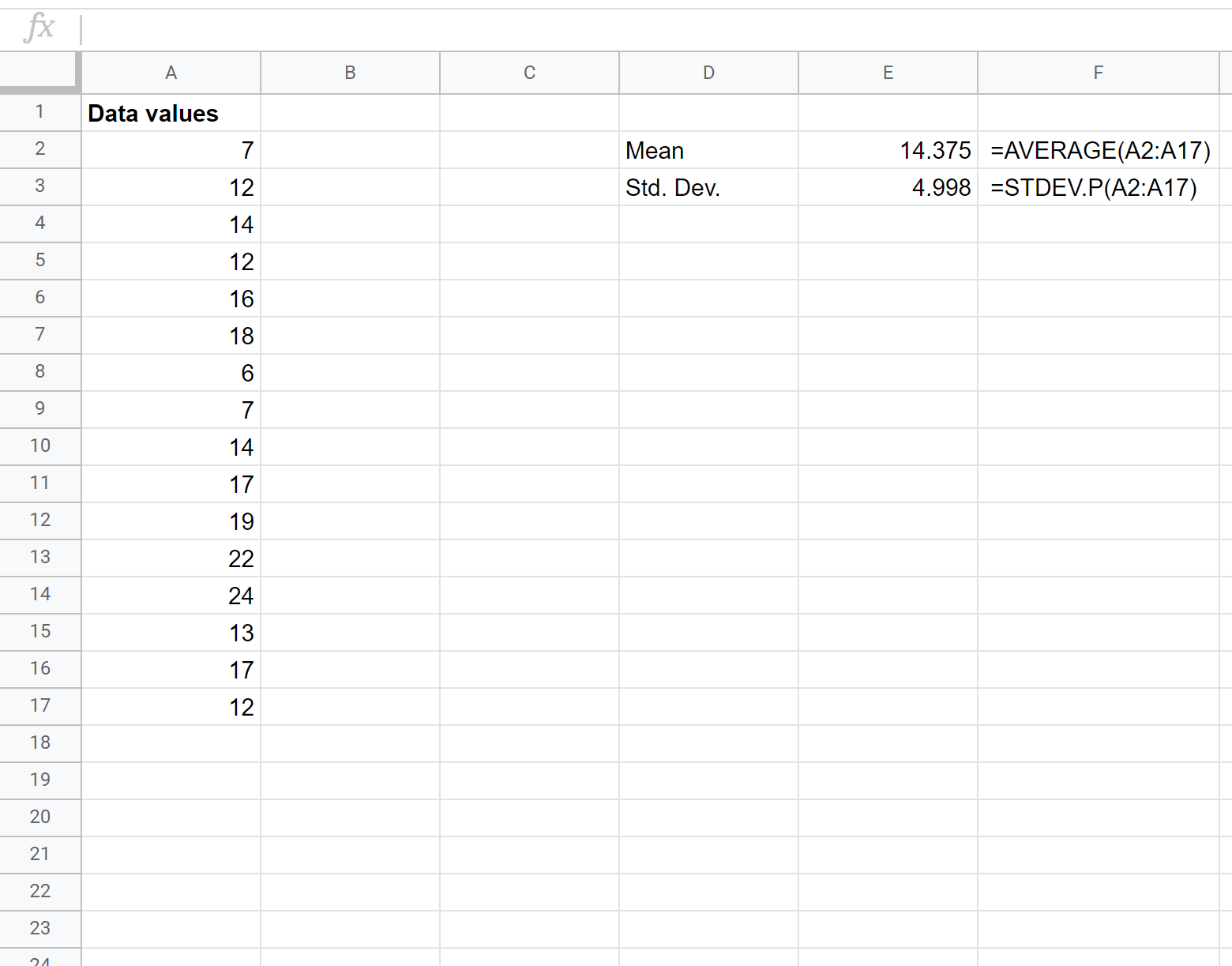
Середнє значення виявляється 14,375 , а стандартне відхилення – 4,998 .

Крок 2. Знайдіть z-показник для першого значення вихідних даних.

Далі ми знайдемо z-показник для першого значення вихідних даних, ввівши таку формулу в клітинку B2:

= ( A2 – $E$2 ) / $E$3

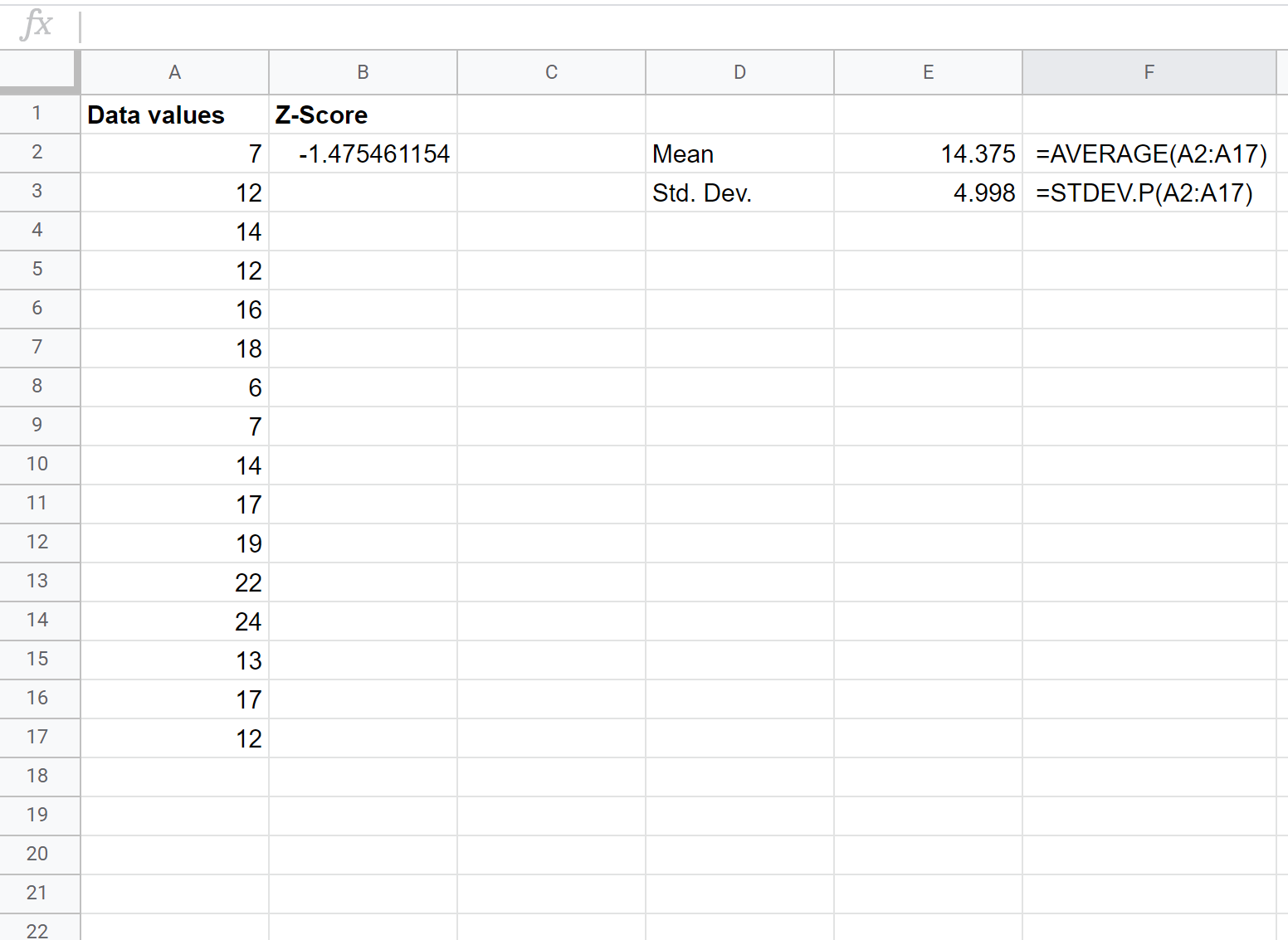
Крок 3. Знайдіть z-оцінки для всіх значень, що залишилися.

Після того, як ми обчислили перший z-показник, ми можемо виділити решту стовпця B, починаючи з клітинки B2, і натиснути Ctrl+D , щоб скопіювати формулу з клітинки B2 до кожної з клітинок нижче:

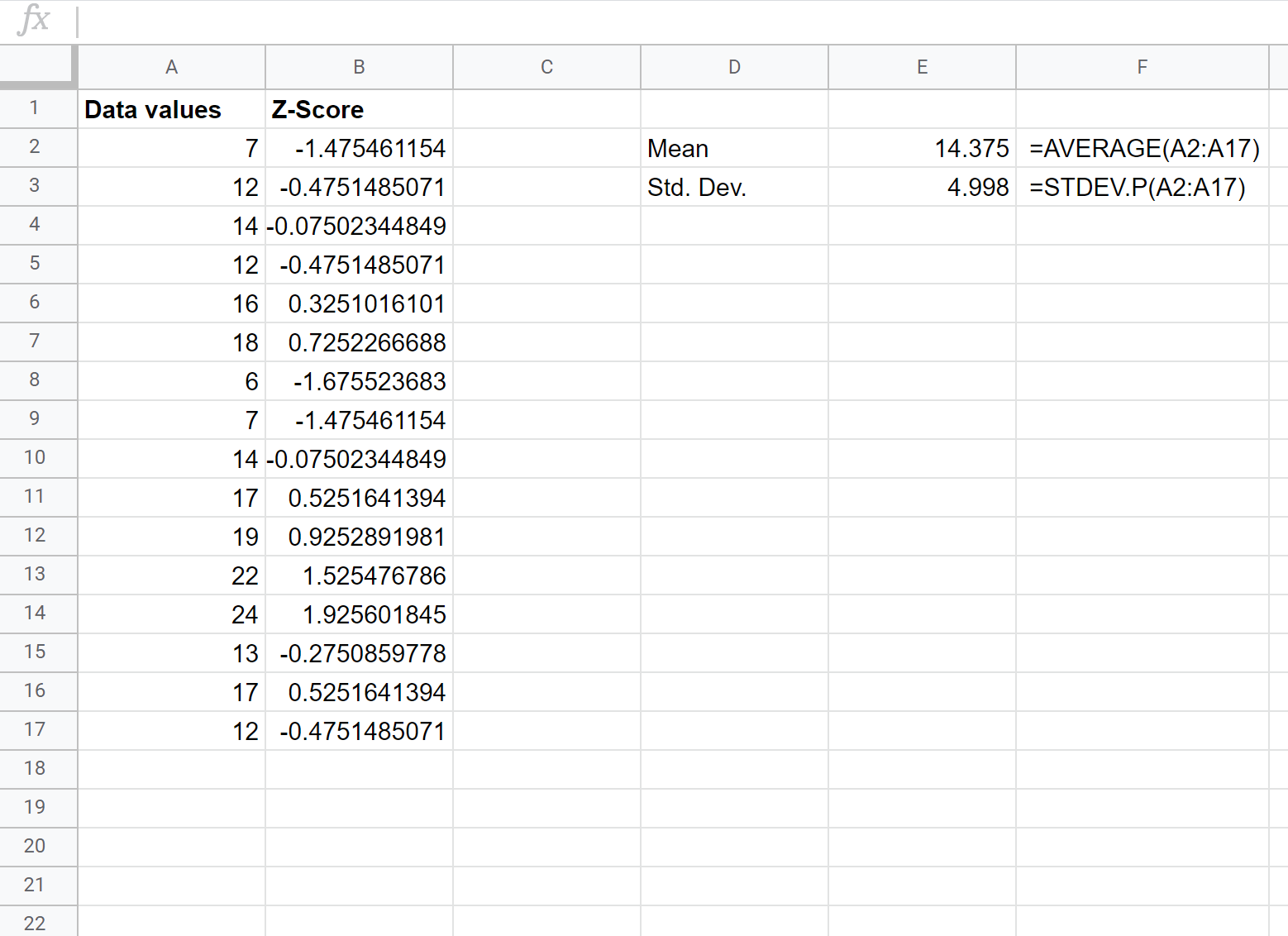
Тепер ми знайшли z-показник для кожного значення вихідних даних.

Як інтерпретувати Z бали

Z-показник просто повідомляє нам, скільки стандартних відхилень має значення від середнього.

У нашому прикладі ми виявили, що середнє значення становило 14,375 , а стандартне відхилення – 4,998 .

Таким чином, перше значення в нашому наборі даних було 7, яке мало z-показник (7-14,375) / 4,998 = -1,47546 . Це означає, що значення «7» на -1,47545 стандартних відхилень нижче середнього.

Наступне значення в наших даних, 12, мало z-показник (12-14,375) / 4,998 = -0,47515 . Це означає, що значення «12» на -0,47515 стандартних відхилень нижче середнього.

Чим далі значення від середнього, тим вищим буде абсолютне значення z-показника для цього значення. Наприклад, значення 7 знаходиться далі від середнього (14,375), ніж значення 12, що пояснює, чому 7 мав z-показник із вищим абсолютним значенням.

Додаткові ресурси

Як обчислити Z-оцінки в Excel
Як розрахувати Z бали в R
Як розрахувати Z-оцінки на калькуляторі TI-84