Аналіз основних компонентів у r: покроковий приклад

Аналіз головних компонентів, часто скорочено PCA, — це техніка машинного навчання без контролю , яка прагне знайти головні компоненти — лінійні комбінації вихідних предикторів, — які пояснюють значну частину варіації в наборі даних.

Мета PCA полягає в тому, щоб пояснити більшість мінливості в наборі даних з меншою кількістю змінних, ніж вихідний набір даних.

Для заданого набору даних із p змінними ми могли б перевірити діаграми розсіювання кожної попарної комбінації змінних, але кількість діаграм розсіювання може стати великою дуже швидко.

Для p предикторів існують p(p-1)/2 хмари точок.

Отже, для набору даних із p = 15 предикторами буде 105 різних діаграм розсіювання!

На щастя, PCA пропонує спосіб знайти низькорозмірне представлення набору даних, яке охоплює якомога більше варіацій у даних.

Якщо ми зможемо охопити більшість варіацій лише у двох вимірах, ми зможемо спроектувати всі спостереження з вихідного набору даних на просту діаграму розсіювання.

Основні компоненти ми знаходимо наступним чином:

_{Дано набір даних із} p _{предикторами} : _

• _{Z m = ΣΦ jm _}
• Z ₁ — це лінійна комбінація предикторів, яка фіксує якомога більшу дисперсію.
• Z ₂ є наступною лінійною комбінацією предикторів, яка фіксує найбільшу дисперсію, будучи ортогональною (тобто некорельованою) до Z ₁ .
• Тоді Z ₃ є наступною лінійною комбінацією предикторів, яка фіксує найбільшу дисперсію, будучи ортогональною до Z ₂ .
• І так далі.

На практиці ми використовуємо такі кроки для обчислення лінійних комбінацій вихідних предикторів:

1. Масштабуйте кожну зі змінних, щоб мати середнє значення 0 і стандартне відхилення 1.

2. Розрахувати коваріаційну матрицю для масштабованих змінних.

3. Обчислити власні значення коваріаційної матриці.

Використовуючи лінійну алгебру, ми можемо показати, що власний вектор, який відповідає найбільшому власному значенню, є першою головною компонентою. Іншими словами, ця конкретна комбінація предикторів пояснює найбільшу дисперсію в даних.

Власний вектор, що відповідає другому за величиною власному значенню, є другим головним компонентом і так далі.

Цей підручник надає покроковий приклад того, як виконати цей процес у R.

Крок 1. Завантажте дані

Спочатку ми завантажимо пакет Tidyverse , який містить кілька корисних функцій для візуалізації та обробки даних:

 library (tidyverse)

Для цього прикладу ми використаємо набір даних USArrests , вбудований у R, який містить кількість арештів на 100 000 жителів у кожному штаті США у 1973 році за вбивства , напади та зґвалтування .

Він також включає відсоток населення кожного штату, що проживає в містах, UrbanPop .

Наступний код показує, як завантажити та відобразити перші рядки набору даних:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

Крок 2: Обчисліть головні компоненти

Після завантаження даних ми можемо використати вбудовану функцію R prcomp() для обчислення основних компонентів набору даних.

Перед обчисленням основних компонентів обов’язково вкажіть scale = TRUE , щоб кожна зі змінних у наборі даних масштабувалася до середнього значення 0 і стандартного відхилення 1.

Також зауважте, що власні вектори в R за замовчуванням вказують у негативному напрямку, тому ми помножимо на -1, щоб змінити знаки.

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

Ми бачимо, що перший головний компонент (PC1) має високі значення для вбивства, нападу та зґвалтування, що вказує на те, що цей головний компонент описує найбільшу варіацію цих змінних.

Ми також бачимо, що другий основний компонент (PC2) має високе значення для UrbanPop, що вказує на те, що цей головний компонент акцентує увагу на міському населенні.

Зауважте, що оцінки основного компонента для кожного стану зберігаються в results$x . Ми також помножимо ці оцінки на -1, щоб змінити знаки:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

Крок 3: Візуалізуйте результати за допомогою біплоту

Далі ми можемо створити біплот – графік, який проектує кожне зі спостережень у наборі даних на діаграму розсіювання, яка використовує перший і другий головні компоненти як осі:

Зауважте, що scale = 0 гарантує, що стрілки на графіку масштабуються відповідно до навантажень.

 biplot(results, scale = 0 )

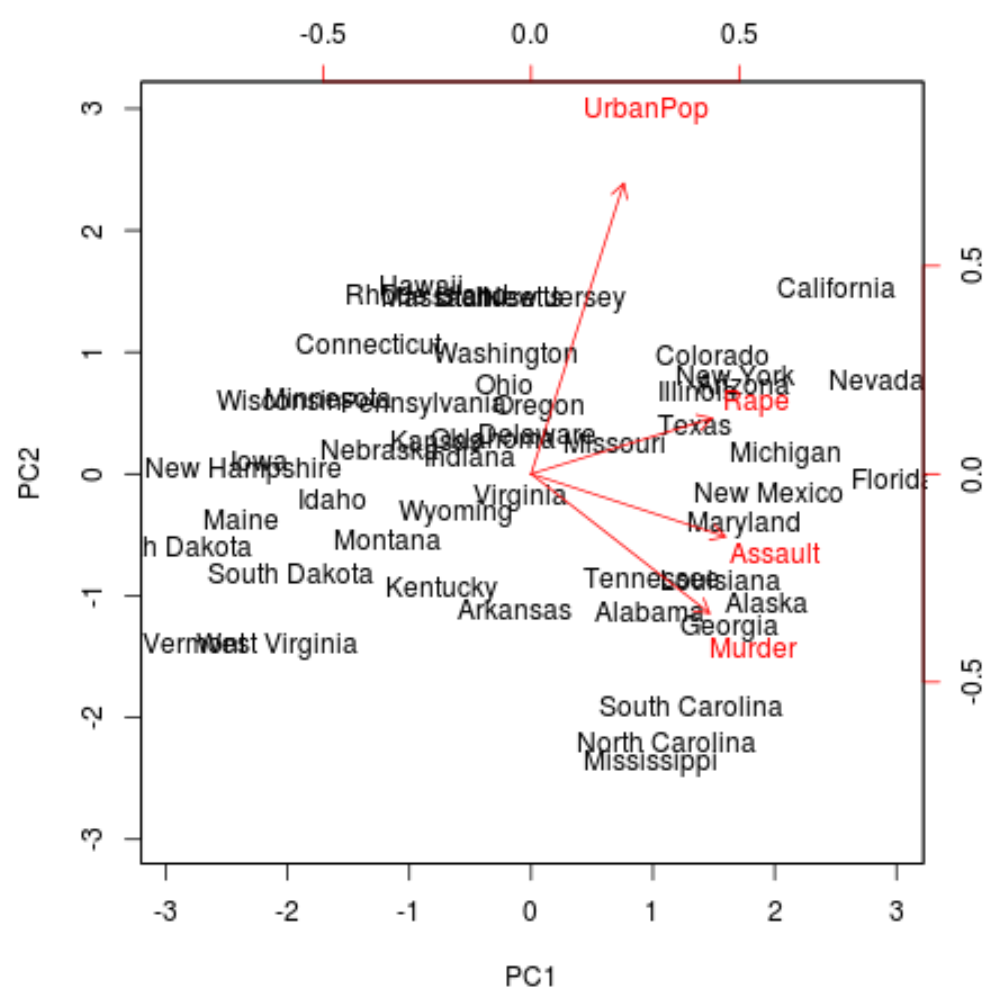
На сюжеті ми можемо побачити кожне з 50 станів, представлених у простому двовимірному просторі.

Стани, близькі один до одного на графіку, мають схожі моделі даних щодо змінних у вихідному наборі даних.

Ми також бачимо, що деякі держави сильніше пов’язані з певними злочинами, ніж інші. Наприклад, Джорджія є штатом, найближчим до змінної Вбивства в сюжеті.

Якщо ми подивимося на штати з найвищим рівнем вбивств у вихідному наборі даних, ми побачимо, що Грузія фактично очолює список:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

Крок 4: Знайдіть дисперсію, пояснену кожним головним компонентом

Ми можемо використати такий код, щоб обчислити загальну дисперсію у вихідному наборі даних, що пояснюється кожним головним компонентом:

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

З результатів ми можемо спостерігати наступне:

• Перший головний компонент пояснює 62% загальної дисперсії в наборі даних.
• Другий головний компонент пояснює 24,7% загальної дисперсії в наборі даних.
• Третій головний компонент пояснює 8,9% загальної дисперсії в наборі даних.
• Четвертий головний компонент пояснює 4,3% загальної дисперсії в наборі даних.

Таким чином, перші два основні компоненти пояснюють більшу частину загальної дисперсії в даних.

Це хороший знак, тому що попередній біплот проектував кожне спостереження з вихідних даних на діаграму розсіювання, яка враховувала лише перші два головних компоненти.

Таким чином, є дійсним вивчити шаблони в біплоті, щоб ідентифікувати стани, які схожі один на одного.

Ми також можемо створити діаграму осипів – графік, який відображає загальну дисперсію, пояснену кожним головним компонентом – для візуалізації результатів PCA:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

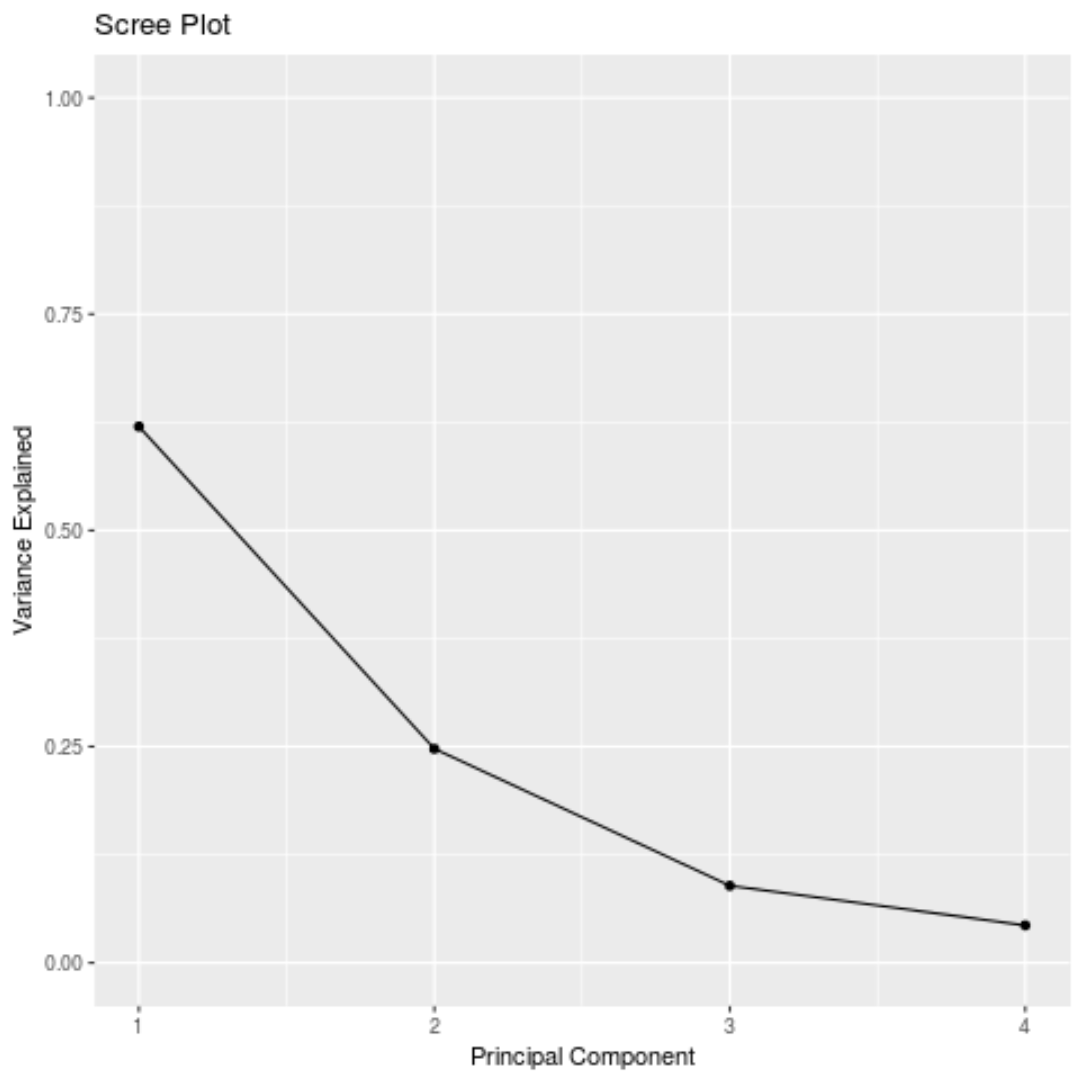
Аналіз головних компонент на практиці

На практиці PCA використовується найчастіше з двох причин:

1. Дослідницький аналіз даних . Ми використовуємо PCA, коли вперше досліджуємо набір даних і хочемо зрозуміти, які спостереження в даних найбільш подібні одне до одного.

2. Регресія головних компонентів – Ми також можемо використовувати PCA для обчислення головних компонентів, які потім можна використовувати в регресії головних компонентів . Цей тип регресії часто використовується, коли існує мультиколінеарність між предикторами в наборі даних.

Повний код R, використаний у цьому посібнику, можна знайти тут .