Вступ до ancova (дисперсійний аналіз)

ANCOVA розшифровується як «аналіз коваріації». Щоб зрозуміти, як працює ANCOVA, спочатку потрібно зрозуміти ANOVA.

ANOVA _   (дисперсійний аналіз) використовується для визначення того, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

Наприклад, скажімо, ми хочемо знати, чи впливає техніка навчання на результати іспитів у класі студентів. Ми розділили клас на три групи випадковим чином. Кожна група використовує різну методику навчання протягом місяця для підготовки до іспиту. Наприкінці місяця всі учні складають однаковий іспит.

Щоб з’ясувати, чи техніка навчання впливає на результати іспитів, ми можемо виконати односторонній дисперсійний аналіз, який покаже нам, чи є статистично значуща різниця між середніми оцінками трьох груп.

ANCOVA — це розширення дисперсійного аналізу ANOVA, у якому ми хочемо визначити, чи існує статистично значуща різниця між трьома чи більше незалежними групами після врахування однієї чи кількохковаріат .

Коваріата — це безперервна змінна, яка змінюється разом зі змінною відповіді.

Наприклад, скажімо, ми хочемо знати, чи впливає техніка навчання на результати іспиту, але ми хочемо взяти до уваги оцінку, яку студент уже має в класі . Ми можемо використовувати їх поточну оцінку як коваріату та виконати ANCOVA, щоб визначити, чи існує статистично значуща різниця між середніми оцінками трьох груп.

Це дає нам змогу перевірити, чи впливає техніка навчання на результати іспиту, коли вплив коваріати буде усунено.

Отже, якщо ми виявимо, що існує статистично значуща різниця в балах за іспит між трьома методами навчання, ми можемо бути впевнені, що ця різниця існує навіть після врахування поточної оцінки студентів у класі (c ‘тобто, якщо вони вже почуваються добре або якщо вони вже почуваються добре). не на уроці) .

Припущення ANCOVA

Перш ніж виконувати ANCOVA, важливо переконатися, що виконуються такі припущення:

• Коваріата (змінні) і факторна змінна (змінні) є незалежними – Коваріата та факторна змінна мають бути незалежними одна від одної, тому що додавання члена коваріати в модель має сенс, лише якщо коваріата та факторна змінна діють незалежно на змінна відповіді.
• Коваріата(и) є безперервними даними. Коваріати мають бути неперервними (тобто дані інтервалу або співвідношення).
• Однорідність дисперсій – дисперсії між групами мають бути приблизно рівними.
• Незалежність – спостереження в кожній групі мають бути незалежними.
• Нормальність – дані повинні бути приблизно нормально розподілені в кожній групі.
• Ніяких екстремальних викидів – у жодній із груп не повинно бути екстремальних викидів, які могли б суттєво вплинути на результати ANCOVA.

ANCOVA: приклад

Викладач хоче знати, чи три різні методи навчання впливають на результати іспиту, але він хоче взяти до уваги поточну оцінку, яку студент уже має в класі.

Він виконає ANCOVA з використанням таких змінних:

• Факторна змінна: технічне дослідження
• Коваріант: поточний бал
• Змінна відповіді: іспитовий бал

У наступній таблиці представлено набір даних 15 студентів, залучених для участі в дослідженні:

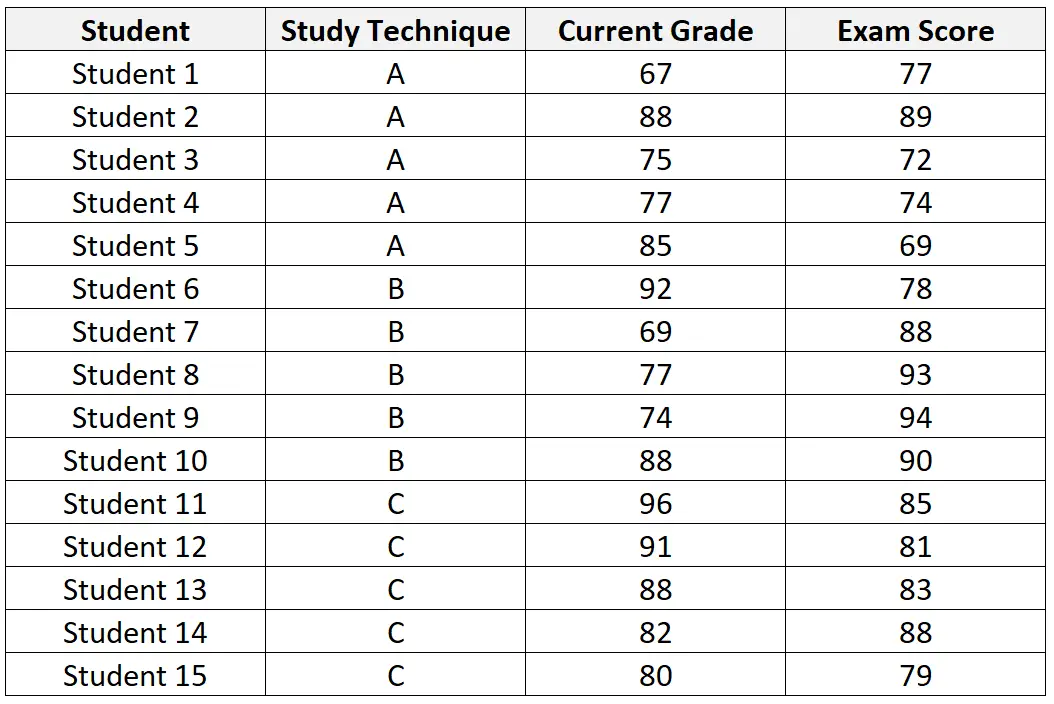
Після виконання ANCOVA на наборі даних викладач отримує такі результати:

P-значення для методики дослідження становить 0,03155 . Оскільки це значення менше 0,05, ми можемо відхилити нульову гіпотезу про те, що кожен із методів навчання призводить до однакової середньої оцінки іспиту, навіть якщо врахувати поточну оцінку студента в класі .

Щоб точно визначити, які методи навчання дають різні середні оцінки іспиту, вчителю потрібно буде провести пост-хок тестування .

Додаткові ресурси

Як виконати ANCOVA в Excel
Як виконати ANCOVA в R
Як виконати ANCOVA в Python
Відмінності між ANOVA, ANCOVA, MANOVA та MANCOVA