Як обчислити асиметрію та ексцес у r

У статистиці асиметрія та ексцес є двома способами вимірювання форми розподілу.

Асиметрія – це міра асиметрії розподілу. Це значення може бути позитивним або негативним.

• Від’ємна асиметрія вказує на те, що хвіст знаходиться на лівій стороні розподілу, який розширюється до більш негативних значень.
• Позитивний перекіс вказує на те, що хвіст знаходиться на правій стороні розподілу, який розширюється до більш позитивних значень.
• Значення нуль вказує на те, що в розподілі немає асиметрії, що означає, що розподіл є абсолютно симетричним.

Ексцес – це міра того, чи є розподіл важким чи легким хвостом порівняно з нормальним розподілом .

• Ексцес нормального розподілу дорівнює 3.
• Якщо певний розподіл має ексцес менший за 3, його називають динамічним , що означає, що він має тенденцію створювати менше екстремальних викидів, ніж нормальний розподіл.
• Якщо заданий розподіл має ексцес більше 3, його називають лептокуртичним , тобто він має тенденцію створювати більше викидів, ніж нормальний розподіл.

Примітка. Деякі формули (визначення Фішера) віднімають 3 від ексцесу, щоб полегшити порівняння з нормальним розподілом. Використовуючи це визначення, розподіл матиме більший ексцес, ніж звичайний розподіл, якщо він матиме значення ексцесу більше 0.

У цьому підручнику пояснюється, як обчислити як асиметрію, так і ексцес даного набору даних у R.

Приклад: перекос і сплощення в R

Припустимо, ми маємо наступний набір даних:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Ми можемо швидко візуалізувати розподіл значень у цьому наборі даних, створивши гістограму:

 hist(data, col=' steelblue ') 

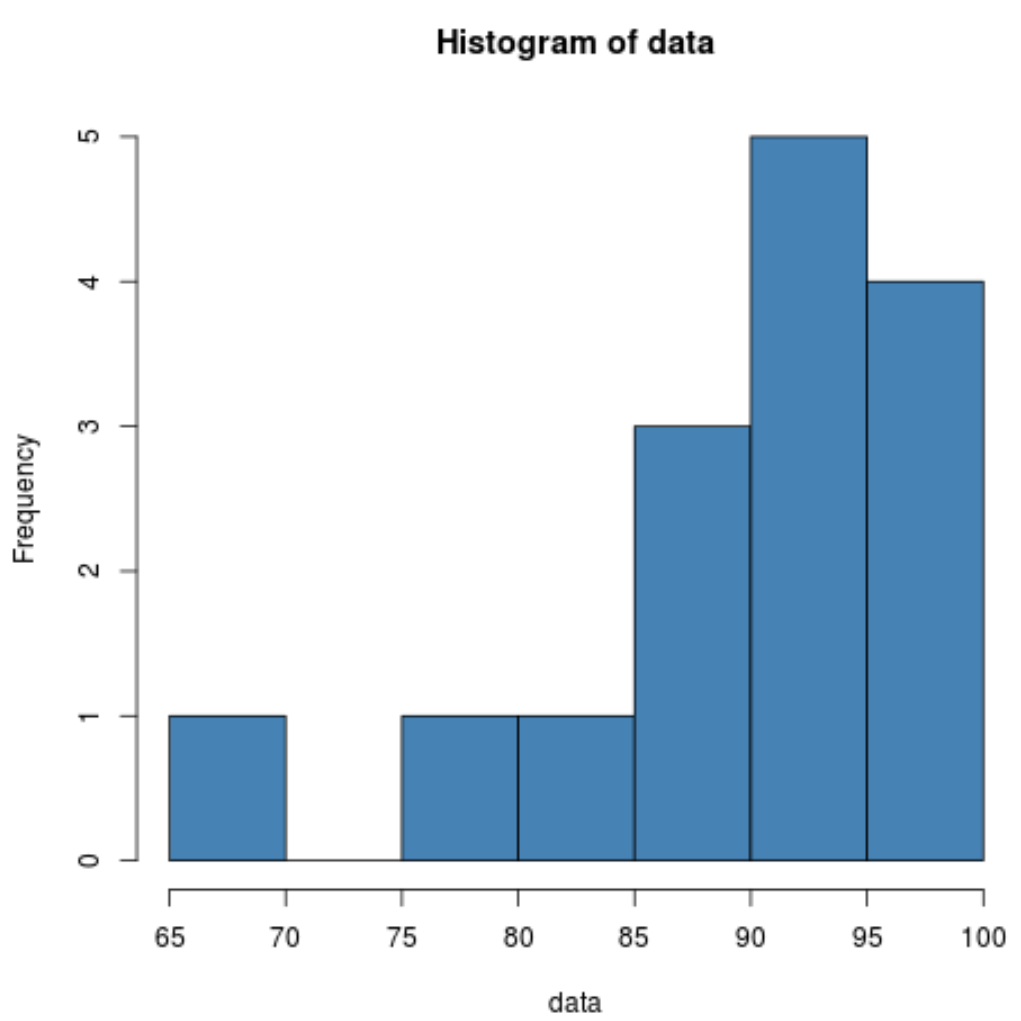
Гістограма показує нам, що розподіл має перекіс вліво. Тобто більша частина значень зосереджена в правій частині розподілу.

Щоб обчислити асимметрию та ексцес цього набору даних, ми можемо використати функції skewness() та ексцес() із бібліотеки моментів у R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

Асиметрія виявляється -1,391777 , а ексцес виявляється 4,177865 .

Оскільки асиметрія від’ємна, це означає, що розподіл є спотвореним. Це підтверджує те, що ми бачили на гістограмі.

Оскільки ексцес більше 3, це означає, що розподіл має більше значень у хвостах порівняно зі звичайним розподілом.

Бібліотека моментів також пропонує функцію jarque.test() , яка виконує перевірку відповідності, яка визначає, чи демонструють вибіркові дані асимметрию та ексцес, що відповідають нормальному розподілу. Нульова та альтернативна гіпотези цього тесту такі:

Нульова гіпотеза : набір даних має асиметрію та ексцес, що відповідає нормальному розподілу.

Альтернативна гіпотеза : набір даних має перекіс і ексцес, що не відповідає нормальному розподілу.

Наступний код показує, як виконати цей тест:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

P-значення тесту виявляється рівним 0,05756 . Оскільки це значення не менше α = 0,05, ми не можемо відхилити нульову гіпотезу. У нас немає достатніх доказів, щоб стверджувати, що цей набір даних має асимметрию та ексцес, відмінні від нормального розподілу.

Ви можете знайти повну документацію Moments Library тут .

Бонус: калькулятор асиметрії та ексцесу

Ви також можете обчислити асиметрію для певного набору даних за допомогою статистичного калькулятора асиметрії та ексцесу , який автоматично обчислює асиметрію та ексцес для заданого набору даних.