Розподіл бернуллі та біноміальний розподіл: у чому різниця?

Випадкова величина відповідає розподілу Бернуллі , якщо вона має лише два можливі результати: 0 або 1.

Наприклад, припустимо, що ми один раз кидаємо монету. Нехай p . Це означає, що ймовірність приземлення хвостів становить 1- p .

Отже, ми могли б написати:

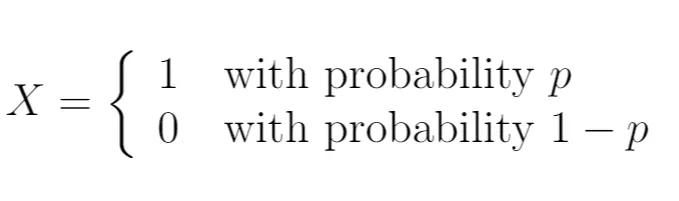
У цьому випадку випадкова величина X відповідає розподілу Бернуллі. Він може приймати лише два можливі значення.

Тепер, якщо ми кидаємо монету кілька разів, сума випадкових величин Бернуллі буде відповідати біноміальному розподілу.

Наприклад, припустімо, що ми кидаємо монету 5 разів і хочемо знати ймовірність отримати голову k разів. Це виглядає як випадкова величина

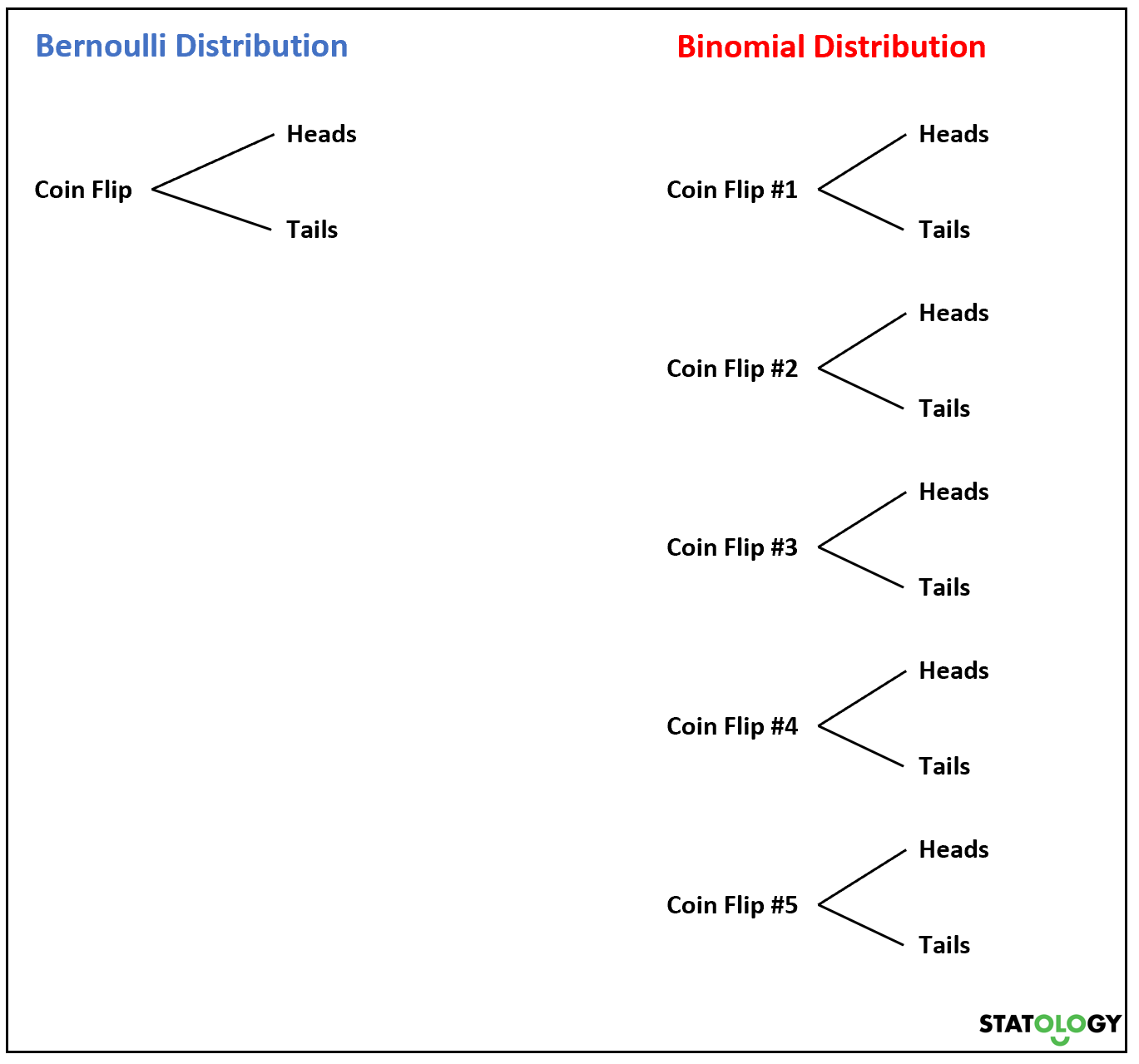
Якщо випадкова величина X відповідає біноміальному розподілу, то ймовірність успіху X = k можна знайти за такою формулою:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

золото:

• n: кількість випробувань
• k: кількість успіхів
• p: ймовірність успіху в даному випробуванні
• _n C _k : кількість способів отримати k успіхів у n випробуваннях

Наприклад, припустимо, що ми кидаємо монету 3 рази. Ми можемо використати наведену вище формулу, щоб визначити ймовірність отримати 0 голів під час цих 3 переворотів:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Коли n = 1 спроба, біноміальний розподіл еквівалентний розподілу Бернуллі.

ВАЖЛИВІ примітки

Ось деякі важливі примітки щодо розподілу Бернуллі та біноміального розподілу:

1. Випадкова величина, яка відповідає розподілу Бернуллі, може приймати лише два можливі значення, але випадкова величина, яка слідує біноміальному розподілу, може приймати кілька значень.

Наприклад, під час одного підкидання монети ми матимемо 0 або 1 голову. Однак у серії з 5 нічиїх ми могли б мати 0, 1, 2, 3, 4 або 5 голів.

2. Щоб випадкова величина відповідала біноміальному розподілу, ймовірність «успіху» в кожному досліді Бернуллі має бути рівною та незалежною.

Наприклад, якщо ми визначаємо «успіх» як приземлення на голови, тоді ймовірність успіху в кожному жеребкуванні дорівнює 0,5, і кожне жеребкування є незалежним – результат жеребкування не впливає на результат іншого.

Додаткові ресурси

Вступ до біноміальних експериментів
Введення в біноміальний розподіл
Розуміння форми біноміального розподілу