Бета-розповсюдження
У цій статті пояснюється, що таке бета-розповсюдження та для чого воно використовується. Так само ви зможете побачити графік бета-розподілу та властивості цього типу розподілу ймовірностей.
Що таке бета-розповсюдження?
Бета-розподіл — це розподіл ймовірностей, визначений на інтервалі (0,1) і параметризований двома позитивними параметрами: α і β. Іншими словами, значення бета-розподілу залежать від параметрів α і β.
Отже, головною особливістю бета-розподілу є те, що його формою можна керувати параметрами α і β. Крім того, бета-розподіл використовується для визначення випадкових змінних, значення яких становить від 0 до 1.
Існує кілька позначень, які вказують на те, що безперервна випадкова змінна регулюється бета-розподілом, найпоширеніші:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ee1d0d8a1624a017b8ef9ce8a67c694e_l3.png)
У статистиці бета-розповсюдження має дуже різноманітне застосування. Наприклад, бета-розподіл використовується для вивчення варіацій у відсотках у різних зразках. Так само в управлінні проектами бета-розповсюдження використовується для виконання аналізу Pert.
Діаграма розподілу бета-версії
Враховуючи визначення бета-розподілу, функція щільності та функція розподілу ймовірностей бета-розподілу зображені нижче.
Нижче ви можете побачити, як змінюється графік функції густини бета-розподілу в залежності від параметрів α і β.
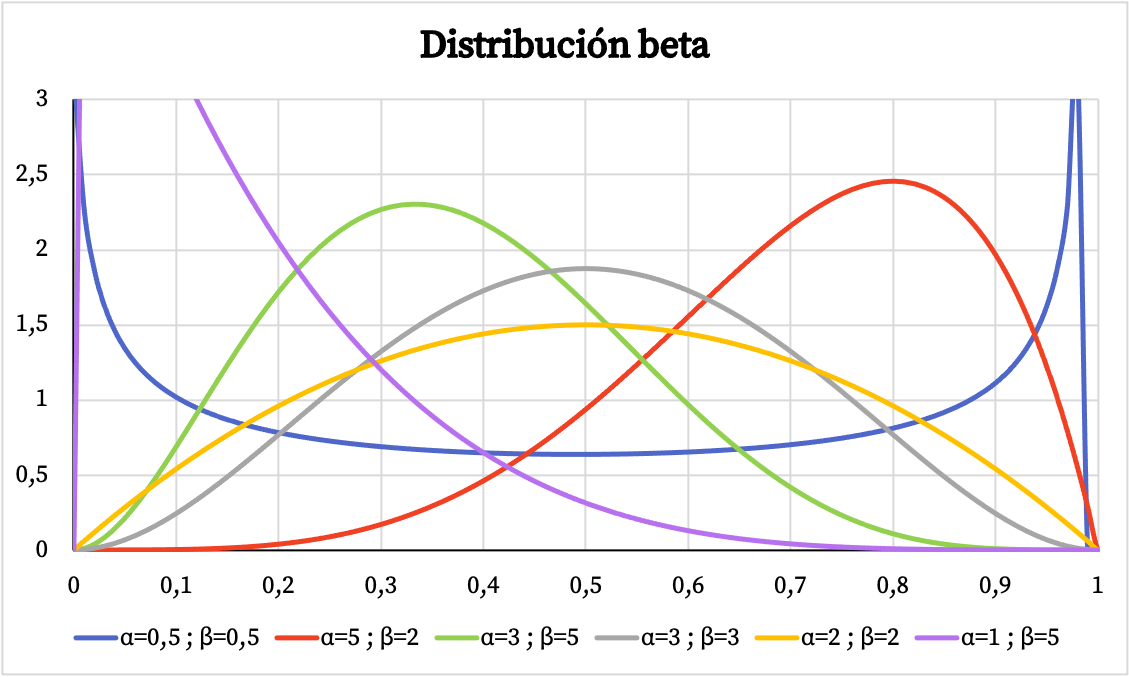
Так само нижче ви можете побачити графічне представлення кумулятивної ймовірності бета-розподілу на основі параметрів α і β.
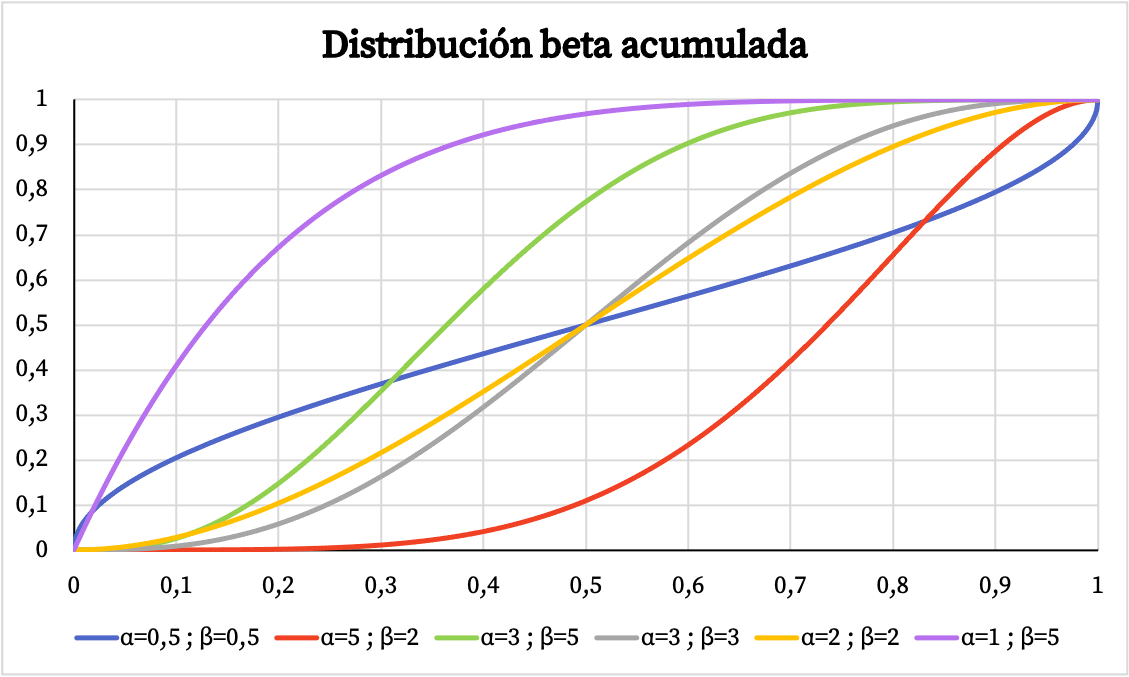
Характеристика бета-розподілу
У цьому розділі ми побачимо, які найважливіші характеристики бета-версії.
- Параметри α і β бета-розподілу є дійсними і додатними числами.
![\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Область бета-розподілу коливається від 0 до 1, два крайні значення не враховуються.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-442bebaba847543d6db71cdf0127a4b0_l3.png)
![]()
- Середнє значення бета-розподілу дорівнює альфа, поділеному на суму альфа плюс бета.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4530a8b72211111e8bec79b6388e00a7_l3.png)
- Дисперсію бета-розподілу можна обчислити за такою формулою:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-71c6ef40db833722e63c56cd763d6601_l3.png)
- Для значень альфа і бета більше 1 режим розподілу бета можна легко знайти за допомогою наступного виразу:
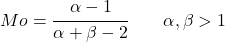
![]()
Де B(α,β) є бета-функцією, яка визначається як:
![]()
- Кумулятивна функція ймовірності бета-розподілу:
![]()
Де B(x;α,β) є неповною бета-функцією, визначеною як:
![]()
- Якщо X є змінною, визначеною бета-розподілом, тоді 1-X є змінною, визначеною бета-розподілом, альфа- та бета-параметри якої є бета- та альфа-параметрами вихідного бета-розподілу відповідно.
![]()
- Якщо обидва альфа- та бета-параметри бета-розподілу дорівнюють 1, тоді розподіл еквівалентний рівномірному розподілу параметрів 0 і 1.
![]()