Що таке бета-рівень у статистиці? (визначення & #038; приклад)

У статистиці ми використовуємо перевірку гіпотез , щоб визначити, чи вірна гіпотеза про параметр сукупності .

Перевірка гіпотези завжди має такі дві гіпотези:

Нульова гіпотеза (H ₀ ): Дані вибірки узгоджуються з домінуючим переконанням щодо параметра сукупності.

Альтернативна гіпотеза ( _HA ): вибіркові дані свідчать про те, що гіпотеза, викладена в нульовій гіпотезі, не відповідає дійсності. Іншими словами, на дані впливає невипадкова причина.

Щоразу, коли ми виконуємо перевірку гіпотези, завжди є чотири можливі результати:

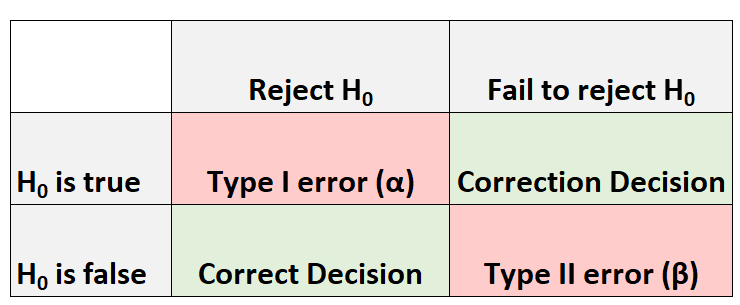
Є два типи помилок, які ми можемо зробити:

• Помилка типу I: ми відкидаємо нульову гіпотезу, коли вона насправді вірна. Імовірність здійснення цього типу помилки позначається α .
• Помилка типу II: ми не можемо відхилити нульову гіпотезу, коли вона насправді хибна. Імовірність такого типу помилки позначається β .

Співвідношення між альфа і бета

В ідеалі дослідники хочуть, щоб імовірність помилки типу I та ймовірність помилки типу II були низькими.

Однак існує компроміс між цими двома ймовірностями. Якщо ми зменшимо альфа-рівень, ми можемо зменшити ймовірність відхилення нульової гіпотези, коли вона насправді вірна, але це фактично збільшить бета-рівень – ймовірність того, що ми не зможемо відхилити нульову гіпотезу, коли вона є неправильною.

Співвідношення між потужністю та бета-версією

Сила перевірки гіпотези стосується ймовірності виявлення ефекту або різниці, коли ефект або різниця насправді присутні. Іншими словами, це ймовірність правильного відхилення хибної нульової гіпотези.

Він розраховується таким чином:

Потужність = 1 – β

Загалом дослідники хочуть, щоб потужність тесту була високою, щоб, якщо є ефект або різниця, тест міг це виявити.

З наведеного вище рівняння ми бачимо, що найкращий спосіб збільшити потужність тесту – це зменшити бета-рівень. І найкращий спосіб зменшити рівень бета-тестування – зазвичай збільшити розмір вибірки.

У наведених нижче прикладах показано, як обчислити бета-рівень перевірки гіпотези, і продемонстровано, чому збільшення розміру вибірки може зменшити бета-рівень.

Приклад 1: обчислення бета-версії для перевірки гіпотези

Припустимо, дослідник хоче перевірити, чи середня вага віджетів, вироблених на фабриці, менше 500 унцій. Ми знаємо, що стандартне відхилення ваг становить 24 унції, і дослідник вирішує зібрати випадкову вибірку з 40 віджетів.

Це реалізує наступну гіпотезу при α = 0,05:

• H ₀ : µ = 500
• H _A : μ < 500

А тепер уявіть, що середня вага виготовлених віджетів фактично становить 490 унцій. Іншими словами, нульову гіпотезу необхідно відкинути.

Ми можемо використати такі кроки, щоб обчислити бета-рівень – ймовірність неспростування нульової гіпотези, коли вона насправді має бути відхилена:

Крок 1. Знайдіть область без відхилення.

Згідно з калькулятором критичного значення Z, ліве критичне значення при α = 0,05 становить -1,645 .

Крок 2: Знайти мінімальний зразок, який ми не зможемо відхилити.

Статистика тесту обчислюється як z = ( x – μ) / (s/ √n )

Отже, ми можемо вирішити це рівняння для вибіркового середнього:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/ √40 )
• х = 493,758

Крок 3: Визначте ймовірність того, що мінімальне середнє значення вибірки дійсно відбудеться.

Ми можемо розрахувати цю ймовірність наступним чином:

• P(Z ≥ (493,758 – 490) / (24/√ 40 ))
• P(Z ≥ 0,99)

Відповідно до звичайного калькулятора CDF ймовірність того, що Z ≥ 0,99, дорівнює 0,1611 .

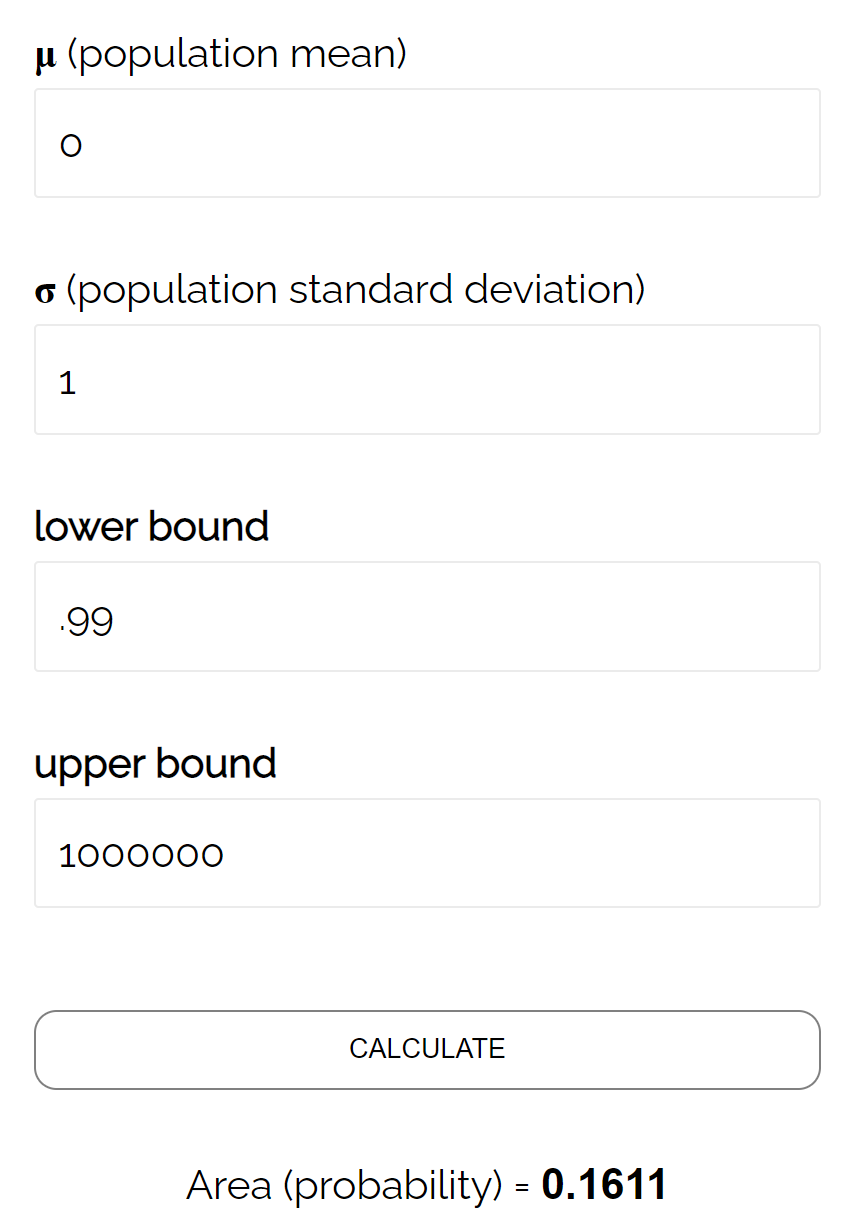
Таким чином, бета-рівень для цього тесту становить β = 0,1611. Це означає, що ймовірність не виявити різницю становить 16,11%, якщо фактичне середнє значення становить 490 унцій.

Приклад 2: обчислення бета-версії для тесту з більшим розміром вибірки

Тепер припустімо, що дослідник виконує точно таку ж перевірку гіпотези, але замість цього використовує вибірку з n = 100 віджетів. Ми можемо повторити ті самі три кроки, щоб обчислити бета-рівень для цього тесту:

Крок 1. Знайдіть область без відхилення.

Згідно з калькулятором критичного значення Z, ліве критичне значення при α = 0,05 становить -1,645 .

Крок 2: Знайти мінімальний зразок, який ми не зможемо відхилити.

Статистика тесту обчислюється як z = ( x – μ) / (s/ √n )

Отже, ми можемо вирішити це рівняння для вибіркового середнього:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/√ 100 )
• х = 496,05

Крок 3: Визначте ймовірність того, що мінімальне середнє значення вибірки дійсно відбудеться.

Ми можемо розрахувати цю ймовірність наступним чином:

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• P(Z ≥ 2,52)

Відповідно до звичайного калькулятора CDF ймовірність того, що Z ≥ 2,52, дорівнює 0,0059.

Таким чином, бета-рівень для цього тесту становить β = 0,0059. Це означає, що ймовірність не виявити різницю становить лише 0,59%, якщо фактичне середнє значення становить 490 унцій.

Зверніть увагу, що просто збільшивши розмір вибірки з 40 до 100, дослідник зміг знизити бета-рівень з 0,1611 до 0,0059.

Бонус: використовуйте цей калькулятор помилок типу II, щоб автоматично обчислити бета-рівень тесту.

Додаткові ресурси

Вступ до перевірки гіпотез
Як написати нульову гіпотезу (5 прикладів)
Пояснення значень P і статистичної значущості