Несхожість брея-кертіса: визначення та приклади

Розбіжність Брея–Кертіса, названа на честь Дж. Роджера Брея та Джона Томаса Кертіса , є способом вимірювання несхожості між двома різними місцями.

Він часто використовується в екології та біології для кількісного визначення різниці між двома ділянками з точки зору видів, знайдених на цих ділянках.

Розбіжність Брея-Кертіса обчислюється наступним чином:

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

золото:

• C _ij : сума найнижчих значень для видів, знайдених на кожному місці.
• S _i : Загальна кількість підрахованих зразків на ділянці i
• S _j : Загальна кількість зразків, підрахованих на ділянці j

Відмінність Брея-Кертіса завжди між 0 і 1, де:

• 0 означає, що два сайти не мають відмінностей. Іншими словами, вони поділяють однакову кількість кожного типу видів.
• 1 вказує на те, що два місця мають повну несхожість. Іншими словами, вони не мають жодного виду одного типу.

У наступному прикладі показано, як обчислити різницю Брея-Кертіса для двох сайтів.

Приклад: розрахунок неподібності Брея-Кертіса

Припустимо, ботанік виходить і підраховує кількість п’яти різних видів рослин (A, B, C, D і E) у двох різних місцях.

У наведеній нижче таблиці підсумовуються дані, які вона зібрала:

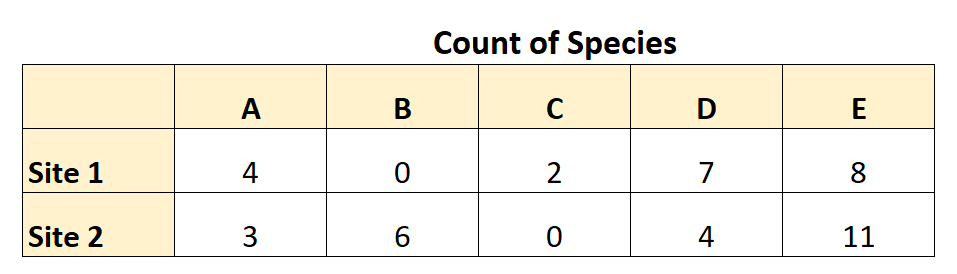
Використовуючи ці дані, вона може обчислити різницю Брей-Кертіса наступним чином:

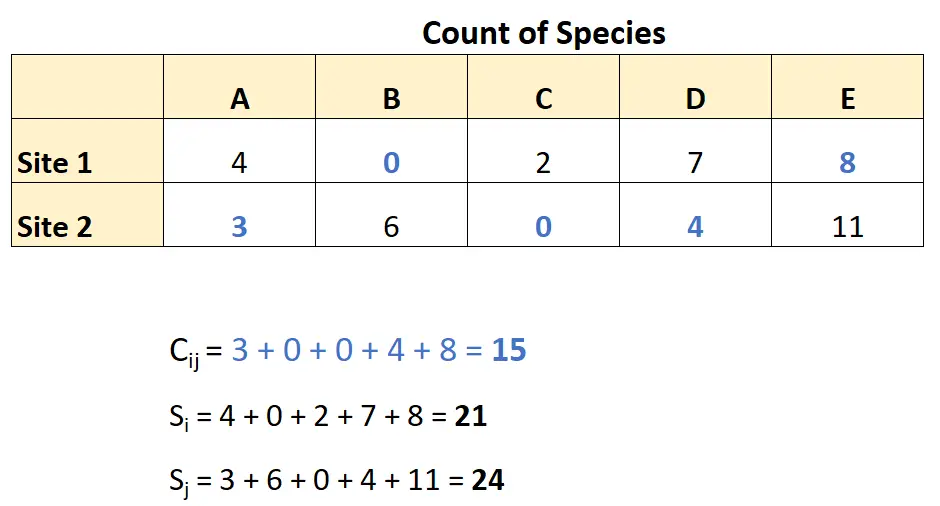
Інтегруючи ці числа у формулу неподібності Брея-Кертіса, ми отримуємо:

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• BC _ij = 0,33

Відмінність Брея-Кертіса між цими двома сайтами становить 0,33 .

Ключове припущення несхожості Брея-Кертіса

Несхожість Брея-Кертіса припускає, що два сайти однакові за розміром.

Це важливе припущення, тому що якщо одна ділянка в чотири рази більша за іншу, ми, природно, матимемо більше видів на більшій ділянці, ніж на меншій, просто тому, що потрібно охопити набагато більше території.

Щоб проілюструвати це, припустімо, що одна з ділянок, для яких ботанік зібрав дані, у чотири рази більша за іншу ділянку:

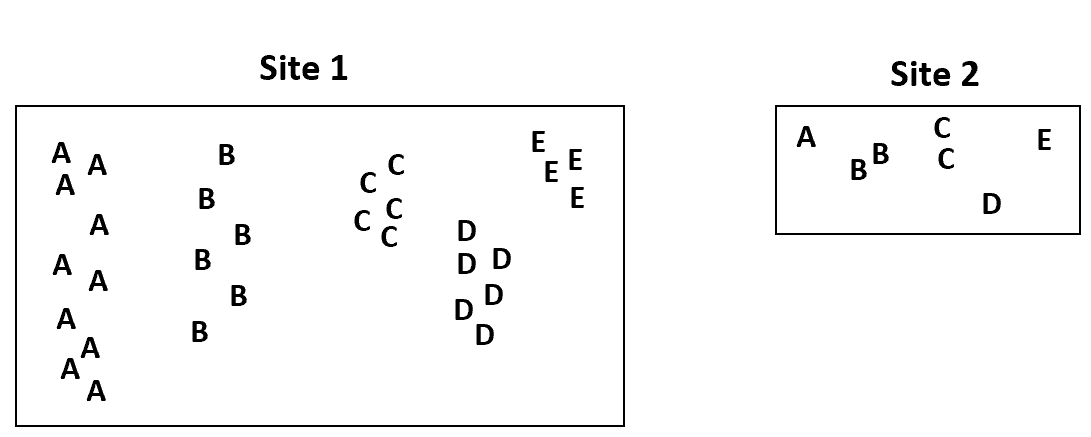
Ми очікували б набагато більшої частоти виду на місці 1 просто тому, що воно набагато більше, ніж місце 2.

Отже, коли ми обчислюємо різницю Брея-Кертіса, вона буде досить великою. Однак це вводить в оману, оскільки різниця між двома сайтами полягає не в їх складі, а скоріше в розмірі.