Біноміальний розподіл

за Редакція 3 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке біноміальний розподіл у статистиці та для чого він використовується. Тому ви знайдете визначення біноміального розподілу, приклади біноміального розподілу та властивості цього типу розподілу ймовірностей. Крім того, ви зможете розрахувати будь-яку ймовірність біноміального розподілу за допомогою онлайн-калькулятора.

Що таке біноміальний розподіл?

Біноміальний розподіл — це розподіл ймовірностей, який підраховує кількість успіхів під час виконання серії незалежних дихотомічних експериментів із постійною ймовірністю успіху.

Іншими словами, біноміальний розподіл — це розподіл, який описує кількість успішних результатів послідовності випробувань Бернуллі.

Пам’ятайте, що тест Бернуллі — це експеримент, який має два можливі результати: «успіх» і «невдача». Отже, якщо ймовірність «успіху» дорівнює p , то ймовірність «невдачі» дорівнює q=1-p .

Загалом, загальна кількість проведених експериментів визначається параметром n , тоді як p є ймовірністю успіху кожного експерименту. Таким чином, випадкова величина, яка слідує за біноміальним розподілом, записується так:

$X\sim\text{Bin}(n,p)$

Зверніть увагу, що в біноміальному розподілі той самий експеримент повторюється n разів, і експерименти не залежать один від одного, тому ймовірність успіху кожного експерименту однакова (p) .

Біноміальний розподіл також можна назвати біноміальним розподілом .

Приклади біноміального розподілу

Ознайомившись із визначенням біноміального розподілу, ми побачимо кілька прикладів змінних, які слідують за цим типом розподілу, щоб краще зрозуміти концепцію.

Кількість разів, коли голови з’являються під час підкидання монети 25 разів.
Кількість кидків, зроблених баскетболістом, коли він кидає в кошик 60 разів з одного місця.
Скільки разів ми отримуємо число 6, кидаючи кубик 30 разів.
Кількість здачі із загальної кількості 50 студентів, які складали іспит.
Кількість бракованих одиниць у вибірці 100 виробів.

Біноміальна формула розподілу

Враховуючи параметри x, n, p, функція ймовірності біноміального розподілу визначається як комбінаторне число n у x , помножене на p ^x , помножене на (1-p) ^nx .

Отже, формула для обчислення ймовірності біноміального розподілу :

👉 Ви можете скористатися наведеним нижче калькулятором, щоб обчислити ймовірність змінної, яка відповідає біноміальному розподілу.

З іншого боку, кумулятивна ймовірність біноміального розподілу обчислюється шляхом додавання ймовірностей кількості розглянутих випадків успіху та всіх попередніх ймовірностей. Отже, формула для обчислення кумулятивної ймовірності біноміального розподілу:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Розв’язана вправа на біноміальний розподіл

Підкидаємо монету 10 разів, яка ймовірність отримати 6 головок?

Змінна в цій задачі відповідає біноміальному розподілу, оскільки всі запуски незалежні один від одного, а також мають однакову ймовірність успіху.

Конкретно ймовірність успіху становить 50%, оскільки лише один із двох можливих результатів вважається успіхом.

$p=\cfrac{1}{2}=0,5$

Отже, розподіл для цієї вправи є біноміальним із загальною кількістю 10 експериментів і ймовірністю 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Отже, щоб визначити ймовірність отримати шість голів, нам потрібно застосувати формулу біноміального розподілу.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Отже, ймовірність отримати рівно шість голів, підкинувши монету десять разів, становить 20,51%.

Характеристика біноміального розподілу

Біноміальний розподіл має такі характеристики:

Біноміальний розподіл визначається двома параметрами: n — загальна кількість експериментів Бернуллі та, з іншого боку, p — ймовірність успіху кожного експерименту Бернуллі.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

Середнє значення біноміального розподілу дорівнює добутку загальної кількості експериментів, помноженої на ймовірність успіху кожного експерименту. Отже, щоб обчислити середнє біноміального розподілу, потрібно помножити n на p .

$E[X]=n\cdot p$

Дисперсія біноміального розподілу дорівнює загальній кількості випробувань, помноженій на ймовірність успіху та ймовірність невдачі.

$Var(X)=n\cdot p\cdot (1-p)$

Формула для функції ймовірності біноміального розподілу має такий вигляд:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Подібним чином формула для кумулятивної функції розподілу біноміального розподілу має вигляд:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Сума двох незалежних біноміальних розподілів з однаковою ймовірністю еквівалентна біноміальному розподілу з тим самим значенням імовірності p і n , що є сумою загальної кількості спроб двох розподілів.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

Розподіл Бернуллі є окремим випадком біноміального розподілу, в якому n=1 , тобто проводиться лише один експеримент.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Якщо _X 1 , _X ₂ ,…, X _k є незалежними випадковими величинами такими, що

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

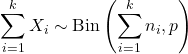
Калькулятор біноміального розподілу

Введіть значення параметрів p, n і x біноміального розподілу в наступний калькулятор, щоб обчислити ймовірність. Вам потрібно вибрати ймовірність, яку ви хочете обчислити, і ввести числа, використовуючи крапку як десятковий роздільник, наприклад 0,1667.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше