Чому медіана важлива в статистиці?

Медіана представляє середнє значення набору даних, коли всі значення впорядковані від найменшого до найбільшого.

Наприклад, медіана в наступному наборі даних становить 19:

Набір даних: 3, 4, 11, 15, 19 , 22, 23, 23, 26

Медіана також представляє ^50-й процентиль набору даних. Тобто рівно половина значень у наборі даних вище медіани, а половина значень — нижче.

Медіана є важливим показником для обчислення, оскільки вона дає нам уявлення про те, де знаходиться «центр» набору даних. Це також дає нам уявлення про «типове» значення в даному наборі даних.

Наприклад, скажімо, у нас є набір даних, що містить ціни продажу 10 000 різних будинків у певному місті.

Замість перегляду рядків і рядківвихідних даних ми можемо обчислити середнє значення, щоб швидко зрозуміти середню ціну продажу будинків у цьому місті.

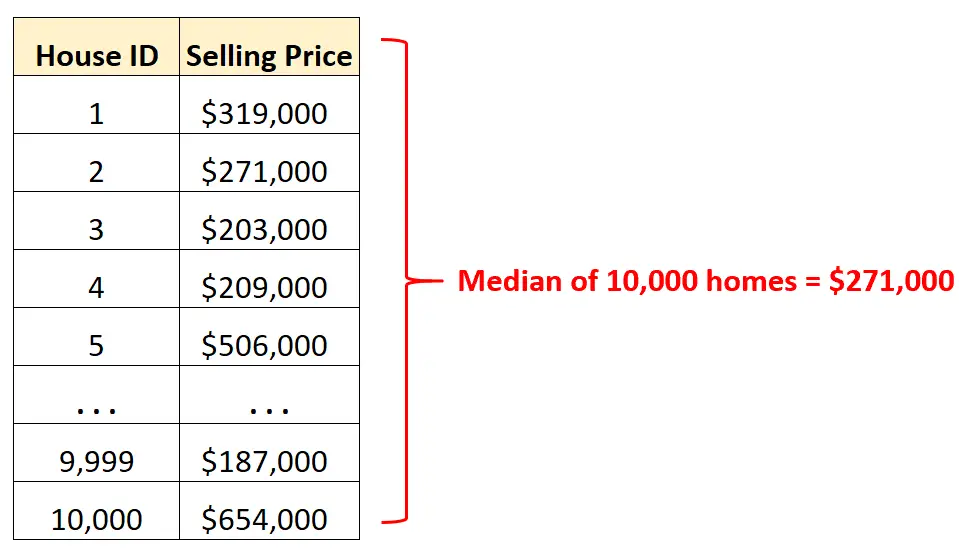
Знаючи, що середня ціна продажу становить 271 000 доларів США, ми знаємо, що рівно половина з 10 000 будинків продана за цю суму дорожче, а інша половина – за менше.

Це також дає нам уявлення про «типову» ціну продажу будинків у цьому місті.

Коли використовувати медіану

Аналізуючи набори даних, ми часто хочемо зрозуміти, де лежить центральна цінність.

У статистиці є два загальні показники, які ми використовуємо для вимірювання центру набору даних:

• Середнє : середнє значення в наборі даних
• Медіана : середнє значення в наборі даних

Виявляється, медіана є більш корисним показником за таких обставин:

• Коли розподіл несиметричний .
• Коли розподіл містить викиди.

Щоб проілюструвати це, розглянемо наступні два приклади.

Приклад 1: обчислення медіани нерівного розподілу

Розглянемо наступний розподіл зарплат жителів певного міста:

Медіана краще відображає «типову» зарплату жителя, ніж середня, оскільки розподіл зміщений вправо.

Це означає, що висока заробітна плата в правій частині розподілу відсуває середнє значення від центру розподілу.

У цьому конкретному прикладі середня зарплата становить 47 000 доларів США, а середня зарплата – 32 000 доларів США. Медіана набагато більше відповідає типовій зарплаті в цьому місті.

Приклад 2: обчислення медіани за наявності викидів

Розглянемо наступний графік, який показує площу будинків на певній вулиці:

На середнє значення сильно впливають кілька надзвичайно великих будинків, а на медіану – ні.

Ми бачимо, що медіана краще фіксує «типову» площу будинку на цій вулиці, ніж середня, оскільки на неї не впливають викиди.

Резюме

Ось короткий виклад основних моментів, розглянутих у цій статті:

• Медіана представляє середнє значення в наборі даних.
• Медіана важлива, оскільки вона дає нам уявлення про те, де знаходиться центральне значення в наборі даних.
• Медіана, як правило, корисніша для обчислення, ніж середнє, коли розподіл спотворений і/або має викиди.

Додаткові ресурси

Конкретні приклади: використання середнього значення, медіани та моди
Коли використовувати середнє проти Медіана: з прикладами
Чому режим важливий у статистиці?