Вибірковий розподіл різниці в пропорціях

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, у чому полягає різниця в пропорційному розподілі вибірки та для чого вона використовується в статистиці. Також подано формулу розподілу вибірки різниці в пропорціях та покрокову розв’язану вправу.

Який вибірковий розподіл різниці в пропорціях?

Розподіл вибірки за різницею пропорцій — це розподіл, який є результатом обчислення відмінностей між пропорціями вибірки всіх можливих вибірок із двох різних сукупностей.

Тобто процес отримання вибіркового розподілу різниці в пропорціях полягає, по-перше, у виділенні всіх можливих вибірок із двох різних генеральних сукупностей, по-друге, у визначенні частки кожної вилученої вибірки та, нарешті, у визначенні різниці між усіма пропорції різниця пропорцій. дві популяції. Таким чином, сукупність результатів, отриманих після виконання цих операцій, формує вибірковий розподіл різниці в пропорціях.

вибірковий розподіл різниці в пропорціях

У статистиці різниця в розподілі вибірки пропорцій використовується для обчислення ймовірності того, що різниця між пропорціями вибірки двох випадково відібраних вибірок близька до різниці в пропорціях сукупності.

➤ Див.: Розподіл вибірки пропорції

Формула для вибіркового розподілу різниці пропорцій

Вибірки, відібрані для різниці в розподілі вибірки пропорцій, визначаються біноміальними розподілами , оскільки для практичних цілей пропорція є відношенням успішних випадків до загальної кількості спостережень.

Тим не менш, завдяки центральній граничній теоремі біноміальні розподіли можна наблизити до нормальних розподілів ймовірностей . Таким чином, вибірковий розподіл різниці в пропорціях можна наблизити до нормального розподілу з такими характеристиками:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Примітка. Вибірковий розподіл різниці в пропорціях можна наблизити до нормального розподілу, лише якщо

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Отже, оскільки вибірковий розподіл різниці в пропорціях можна наблизити до нормального розподілу, формула для розрахунку статистики вибіркового розподілу різниці в пропорціях виглядає наступним чином:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

золото:

$\widehat{p_i}$

є пропорцією зразка i.
$p_i$

це частка населення i.
$q_i$

ймовірність відмови популяції i,

$q_i=1-p_i$

.
$n_i$

це розмір вибірки i.
$Z$

є змінною, визначеною стандартним нормальним розподілом N(0,1).

Ця формула подібна до формули перевірки гіпотез для різниці в пропорціях.

Конкретний приклад вибіркового розподілу різниці пропорцій

Ознайомившись із визначенням різниці пропорцій вибіркового розподілу та його формулою, ви можете переглянути нижче розв’язаний приклад крок за кроком, щоб остаточно зрозуміти концепцію.

Ви хочете проаналізувати точність двох виробничих установок, одна фабрика виробляє таким чином, що лише 5% вироблених деталей мають дефекти, тоді як відсоток дефектних деталей іншої фабрики становить 8%. Якщо ми візьмемо зразок з 200 деталей з першої фабрики та ще один зразок з 280 деталей з другої фабрики, яка ймовірність того, що відсоток дефектів на першому заводі буде більшим, ніж відсоток дефектів на другому заводі? виробництво?

Щоб остаточно дізнатися всі дані задачі, ми спочатку обчислимо частку добре вироблених частин кожної рослини:

$\begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}$

Якщо рівень браку на першій фабриці був більшим, ніж рівень браку на другій фабриці, це означає, що наступне рівняння буде вірним:

$\widehat{p_1}-\widehat{p_2}>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”89″ style=”vertical-align: -4px;”> Отже, щоб визначити ймовірність розподілу вибірки різниці в пропорціях, нам потрібно застосувати формулу, пояснену в розділі вище: <p class=$ $Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}=\cfrac{0-(0,05-0,08)}{\displaystyle\sqrt{\frac{0,05\cdot 0,95}{200}+\frac{0,08\cdot 0,92}{280}}}=1,34$

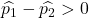
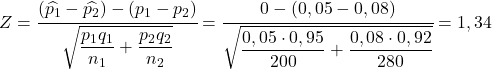
Таким чином, ймовірність того, що рівень дефектів першої фабрики більший, ніж рівень дефектів другої фабрики, еквівалентна ймовірності того, що змінна Z перевищує 1,34:

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”242″ style=”vertical-align: -5px;”> Нарешті, нам просто потрібно знайти відповідну ймовірність у <a href=$ таблиці нормального розподілу , і ми вже розв’яжемо задачу:

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”319″ style=”vertical-align: -5px;”> Коротше кажучи, ймовірність того, що частка дефектів на першій фабриці більша, ніж частка дефектів на другій фабриці, становить 9,01%. <div style=$ ➤ Див.: Вибірковий розподіл різниці середніх

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Який вибірковий розподіл різниці в пропорціях?

Формула для вибіркового розподілу різниці пропорцій

Конкретний приклад вибіркового розподілу різниці пропорцій

Про автора

Редакція

Додати коментар