Вибірковий розподіл середнього

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке вибірковий розподіл середнього значення в статистиці. Ви також знайдете формулу розподілу середньої вибірки та крок за кроком розв’язану вправу.

Що таке вибірковий розподіл середнього значення?

Вибірковий розподіл середнього (або вибірковий розподіл середніх ) — це розподіл, який є результатом обчислення вибіркового середнього кожної можливої вибірки із сукупності. Тобто набір вибіркових середніх із усіх можливих вибірок сукупності формує вибірковий розподіл середнього.

Або іншими словами, якщо ми вивчаємо всі зразки, які можна взяти з генеральної сукупності, і обчислюємо середнє значення кожного з зразків, набір обчислених значень утворює вибірковий розподіл вибіркового середнього.

У статистиці вибірковий розподіл середнього використовується для обчислення ймовірності наближення до значення середнього сукупності при аналізі однієї вибірки.

Формула для вибіркового розподілу середнього

Дано генеральну сукупність, яка відповідає нормальному розподілу ймовірностей із середнім

$\mu$

і стандартне відхилення

$\sigma$

і витягуються зразки розміру

$n$

, вибірковий розподіл середнього також буде визначено нормальним розподілом, що має такі характеристики:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

золото

$\mu_{\overline{x}}$

є середнім значенням вибіркового розподілу середнього значення та

$\sigma_{\overline{x}}$

є його стандартним відхиленням. Крім того,

$\cfrac{\sigma}{\sqrt{n}}$

стандартна помилка розподілу вибірки.

Примітка. Якщо генеральна сукупність не відповідає нормальному розподілу, але розмір вибірки є великим (n>30), вибірковий розподіл середнього також можна наблизити до попереднього нормального розподілу за центральною граничною теоремою.

Отже, оскільки вибірковий розподіл середнього відповідає нормальному розподілу, формула для обчислення будь-якої ймовірності, пов’язаної з вибірковим середнім, має вигляд:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

золото:

$\overline{x}$

це зразок засобів.
$\mu$

Це середній показник населення.
$s$

стандартне відхилення сукупності.
$n$

це розмір вибірки.
$Z$

є змінною, визначеною стандартним нормальним розподілом N(0,1).

Реальний приклад вибіркового розподілу середнього значення

Ознайомившись із визначенням вибіркового розподілу середнього значення та пов’язаними з ним формулами, давайте розв’яжемо приклад, щоб краще зрозуміти концепцію.

Вага студентів університету має нормальний розподіл із середнім значенням 68 кг і стандартним відхиленням 9 кг. Визначено:
1. Яка ймовірність того, що середня вага випадкової вибірки з 25 студентів буде менше 66 кг?
2. Якщо взято 300 зразків по 25 учнів кожна, скільки середніх зразків матиме значення менше 66 кг?

Перш за все, ми повинні обчислити значення відповідної статистики, для цього ми застосовуємо формулу, яку ми бачили вище:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}=\frac{66-68}{\displaystyle\frac{9}{\sqrt{25}}}=-1,11$

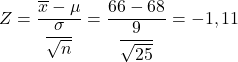
Отже, ймовірність, яку ми шукаємо, відповідає значенню Z=-1,11 лівого хвоста стандартного нормального розподілу, яке можна легко отримати з таблиці ймовірностей Z. Тому ми використовуємо таблицю Z, щоб визначити ймовірність того, що проблема запитує нас:

$P[\overline{x}\leq 66]=P[Z\leq -1,11] =0,1335$

➤ Див.: Таблиця Z

Тепер, коли ми знаємо ймовірність того, що середнє значення випадкової проби менше 66 кг, щоб дізнатися кількість проб, середнє значення менше 66 кг, взявши 300 однакових проб, нам потрібно помножити обчислену ймовірність на загальну кількість взятих проб:

$0,1335\cdot 300 =40,05 \approx 40$

Таким чином, приблизно 40 вилучених зразків матимуть середню вагу менше 66 кг.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке вибірковий розподіл середнього значення?

Формула для вибіркового розподілу середнього

Реальний приклад вибіркового розподілу середнього значення

Про автора

Редакція

Додати коментар