Як інтерпретувати викривлений залишковий графік (з прикладом)

Графіки залишків використовуються для оцінки того, чи нормально розподілені залишки регресійної моделі та чи є вони гетероскедастичними .

В ідеалі ви бажаєте, щоб точки на залишковому графіку були випадковим чином розкидані навколо значення нуля без чіткої моделі.

Якщо ви зіткнулися з залишковим графіком, на якому точки графіка мають криволінійний візерунок, це, ймовірно, означає, що модель регресії, яку ви вказали для даних, є неправильною.

У більшості випадків це означає, що ви намагалися підібрати модель лінійної регресії до набору даних, який натомість слідує квадратичному тренду.

У наступному прикладі показано, як на практиці інтерпретувати (і виправляти) викривлений графік залишків.

Приклад: інтерпретація викривленого залишкового графіка

Припустімо, ми збираємо такі дані про кількість відпрацьованих годин на тиждень і рівень щастя (за шкалою від 0 до 100) для 11 різних людей в офісі:

Якби ми створили просту діаграму розсіювання відпрацьованих годин і рівня щастя, це виглядало б ось як:

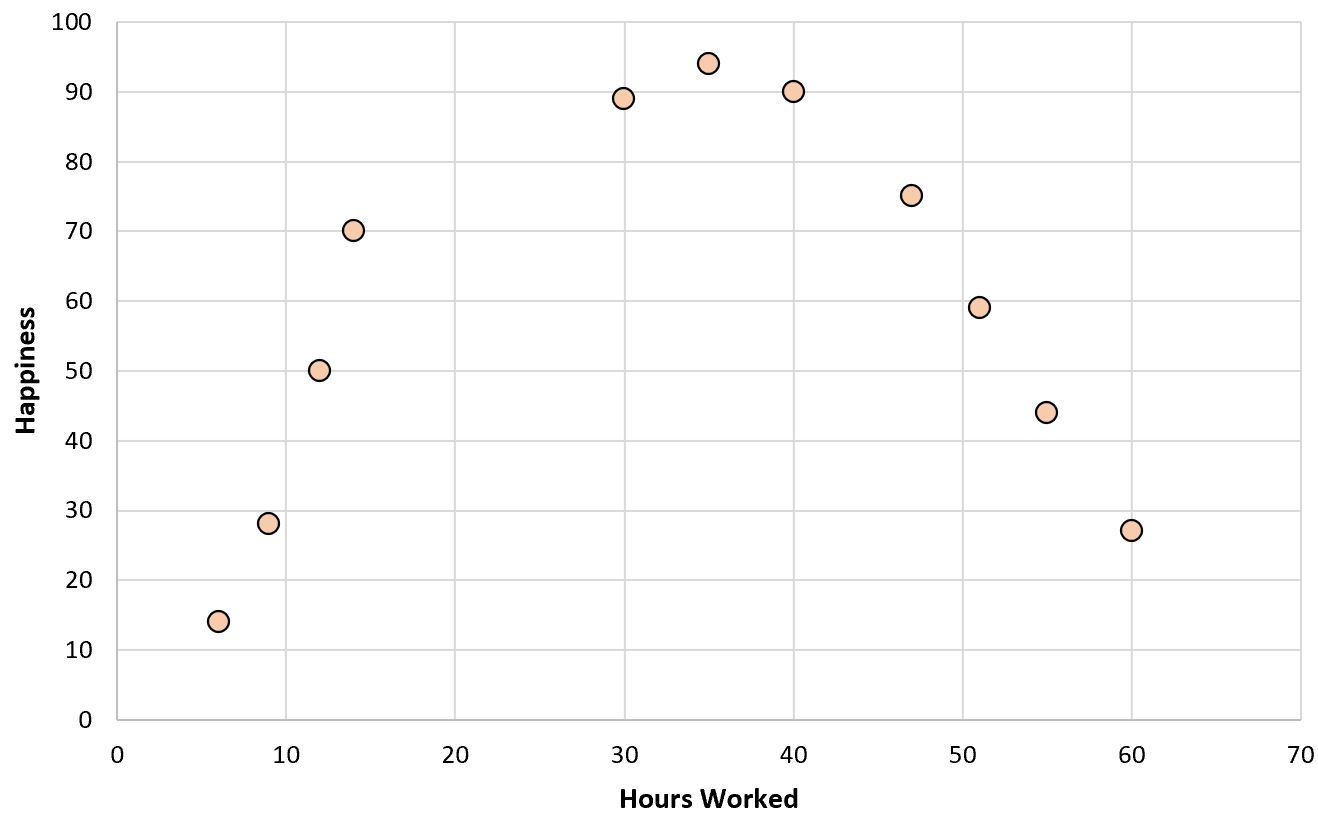
Тепер припустімо, що ми хочемо підібрати регресійну модель, використовуючи відпрацьовані години для прогнозування рівня щастя.

Наступний код показує, як підігнати просту модель лінійної регресії до цього набору даних і створити графік залишків у R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

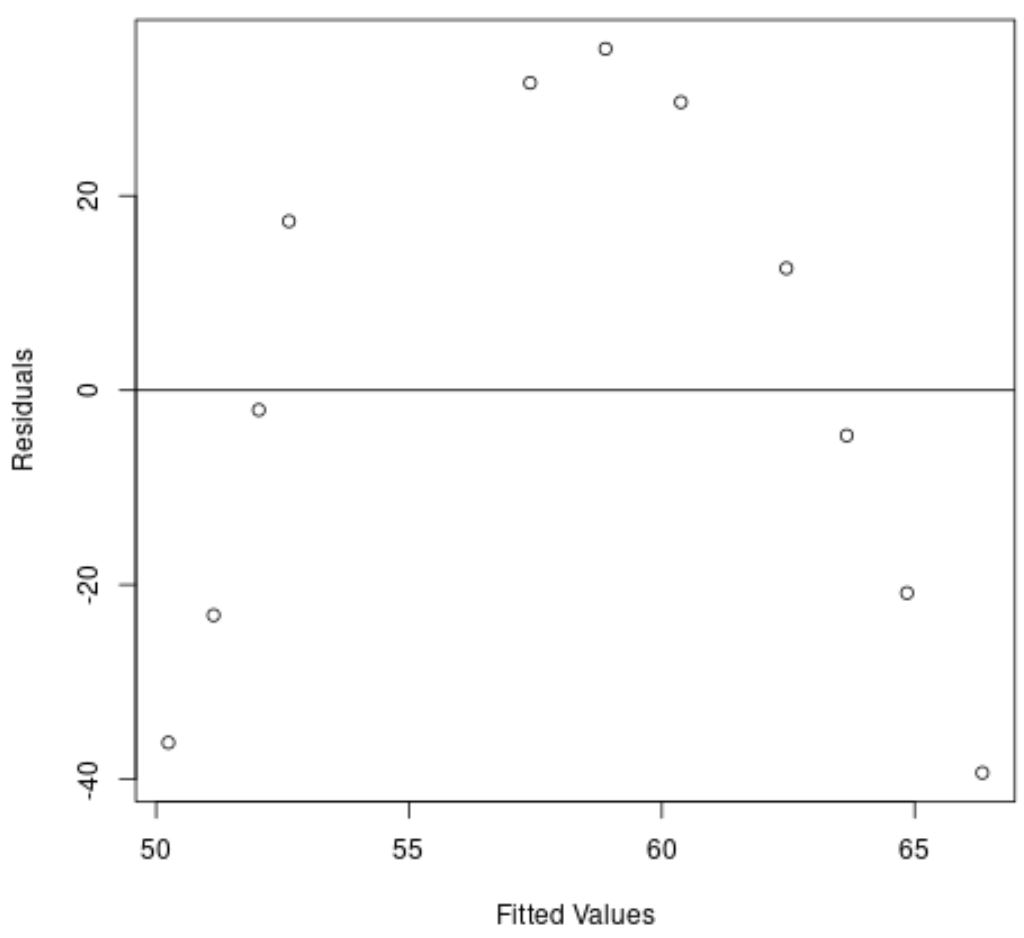
На осі абсцис відображаються підібрані значення, а на осі у – залишки.

На графіку ми бачимо, що залишки мають криву структуру, що вказує на те, що лінійна регресійна модель не забезпечує відповідного підгонки до цього набору даних.

У наведеному нижче коді показано, як підігнати модель квадратичної регресії до цього набору даних і створити графік залишків у R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

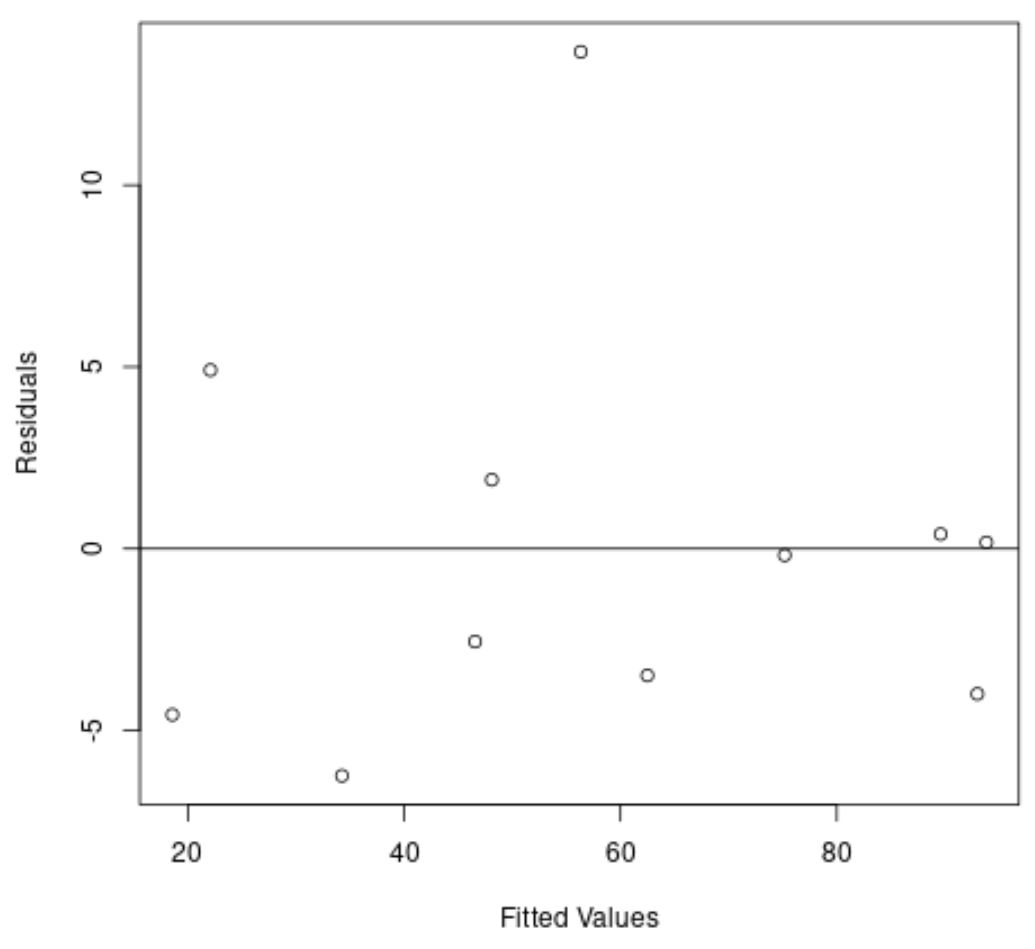
Знову ж таки, вісь х показує підібрані значення, а вісь у – залишки.

На графіку ми бачимо, що залишки випадковим чином розкидані навколо нуля, і немає чіткої тенденції в залишках.

Це говорить нам про те, що модель квадратичної регресії набагато краще підбирає цей набір даних, ніж модель лінійної регресії.

Це має бути сенс, враховуючи, що ми бачили, що справжній зв’язок між відпрацьованими годинами та рівнями щастя виявився квадратичним, а не лінійним.

Додаткові ресурси

У наступних посібниках пояснюється, як створити графіки залишків за допомогою різного статистичного програмного забезпечення:

Як створити залишковий контур вручну
Як створити ділянку залишків у R
Як створити діаграму залишку в Excel
Як створити залишковий графік у Python