Що таке випадкові величини?

Випадкова величина , зазвичай позначається X, – це змінна, можливі значення якої є результатом випадкового процесу.

Випадкові величини бувають двох типів: дискретні та безперервні .

Дискретні випадкові величини

Дискретна випадкова змінна – це така величина, яка може приймати лише лічильну кількість різних значень, наприклад 0, 1, 2, 3, 4, 5…100, 1 мільйон тощо. Ось кілька прикладів дискретних випадкових величин:

• Кількість разів, коли монета потрапляє в решку після 20 підкидань.
• Кількість разів, коли кубик потрапляє на число 4 після 100 кидків.
• Кількість бракованих віджетів в коробці 50 віджетів.

Розподіл ймовірностей для дискретної випадкової величини повідомляє нам про ймовірність того, що випадкова змінна приймає певні значення.

Наприклад, припустімо, що ми один раз кидаємо справедливий кубик. Якщо ми позначимо X ймовірність того, що кубик випаде на певне число, то розподіл ймовірностей можна записати таким чином:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Примітка:

Щоб розподіл ймовірностей був дійсним, він повинен задовольняти наступним двом критеріям:

1. Імовірність кожного результату має бути між 0 і 1.

2. Сума всіх ймовірностей повинна давати 1.

Зверніть увагу, що розподіл ймовірностей для кидка кубика задовольняє обидва ці критерії:

1. Ймовірність кожного результату становить від 0 до 1.

2. Сума всіх ймовірностей дорівнює 1.

Ми можемо використовувати гістограму для візуалізації розподілу ймовірностей:

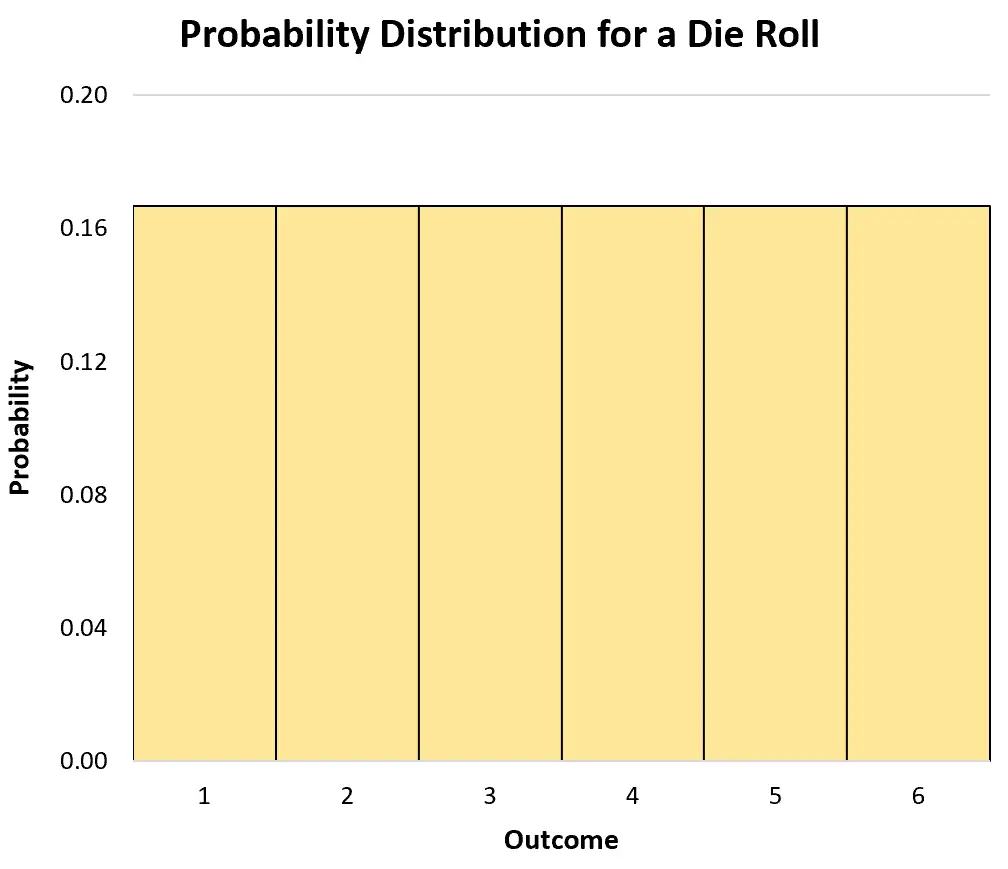
Кумулятивний розподіл ймовірностей для дискретної випадкової змінної повідомляє нам про ймовірність того, що змінна набуде значення , рівного або меншого за певне значення.

Наприклад, кумулятивний розподіл ймовірностей для кидка кубика виглядатиме так:

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

Шанс того, що кубик впаде на одиницю або менше, дорівнює просто 1/6, оскільки він не може впасти на число, менше за одиницю.

Імовірність того, що він приземлиться на двох або менше, становить P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

Подібним чином, ймовірність того, що він приземлиться на трьох або менше, становить P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6, і так далі.

Ми також можемо використовувати гістограму для візуалізації кумулятивного розподілу ймовірностей:

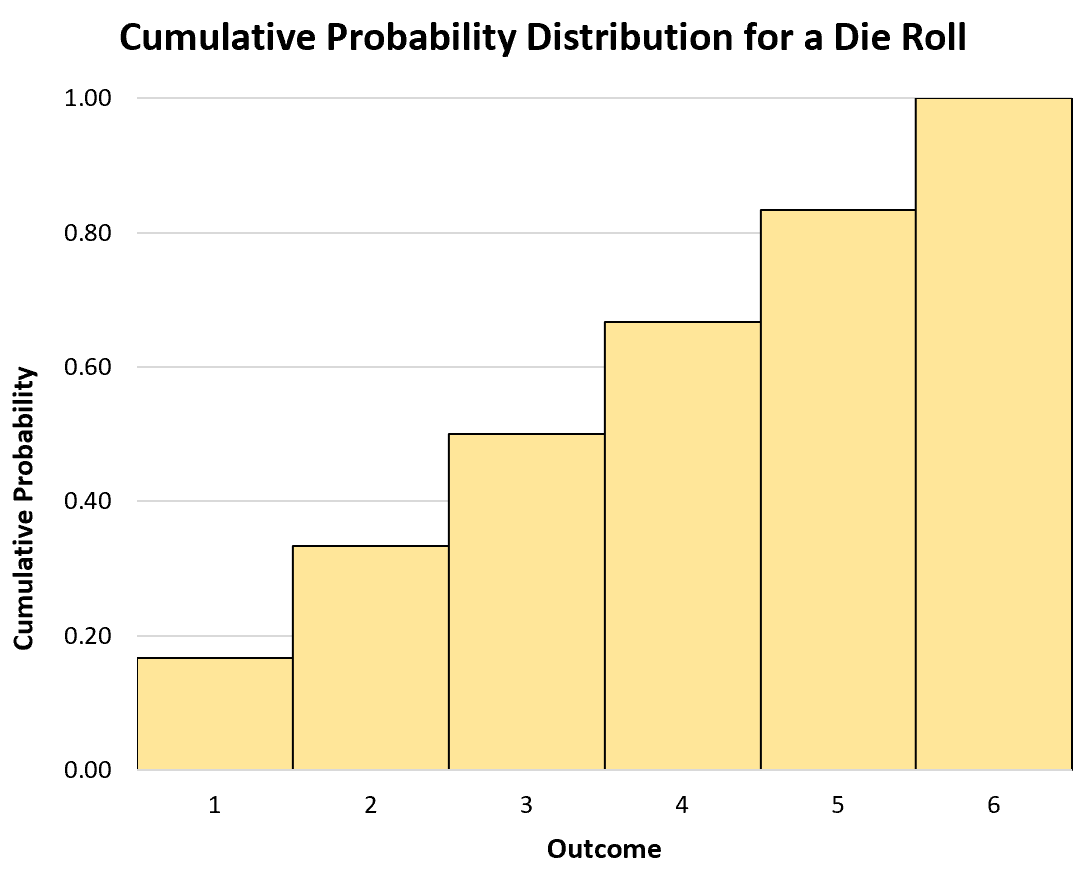
Безперервні випадкові величини

Безперервна випадкова величина — це змінна, яка може набувати нескінченно багато можливих значень. Ось кілька прикладів безперервних випадкових величин:

• Вага тварини
• Зріст людини
• Час, необхідний для марафону

Наприклад, зріст людини може становити 60,2 дюйма, 65,2344 дюйма, 70,431222 дюйма тощо. Існує нескінченна кількість можливих значень розміру.

Загальне правило:

Якщо ви можете порахувати кількість результатів, то ви працюєте з дискретною випадковою змінною, наприклад, підраховуєте, скільки разів монета випадає вгору.

Але якщо ви можете виміряти результат, ви працюєте з безперервною випадковою змінною – наприклад, вимірюєте зріст, вагу, час тощо.

Розподіл ймовірностей для безперервної випадкової величини повідомляє нам про ймовірність того, що випадкова величина приймає певні значення.

Однак, на відміну від розподілу ймовірностей для дискретних випадкових змінних, розподіл імовірностей для безперервної випадкової змінної може використовуватися лише для того, щоб повідомити нам про ймовірність того, що змінна приймає діапазон значень.

Наприклад, припустімо, що ми хочемо знати ймовірність того, що гамбургер із певного ресторану важить чверть фунта (0,25 фунта). Оскільки вага є безперервною змінною, вона може приймати нескінченну кількість значень.

Наприклад, певний гамбургер може важити 0,250001 фунта, або 0,24 фунта, або 0,2488 фунта. Імовірність того, що даний гамбургер важитиме рівно 0,25 фунта, фактично дорівнює нулю.

Таким чином, ми можемо використовувати лише розподіл ймовірностей, щоб повідомити нам ймовірність того, що гамбургер важить менше 0,25 фунтів, більше 0,25 фунтів або в межах певного діапазону (наприклад, між 0,23 фунтів і 0,27 фунтів).

Додаткові ресурси

Наступні посібники надають додаткову інформацію про випадкові змінні:

Що таке випадкові змінні iid?
10 прикладів випадкових величин у реальному житті