Висновок і передбачення: в чому різниця?

Часто в статистиці ми хочемо використовувати дані з однієї з двох причин:

(1) Висновок: ми хочемо зрозуміти природу зв’язку між змінними прогнозу та змінною відповіді в існуючому наборі даних.

(2) Прогноз: ми хочемо використати наявний набір даних для створення моделі, яка передбачає значення змінної відповіді нового спостереження.

Наприклад, припустімо, що ми маємо наступний набір даних, що містить інформацію про будинки:

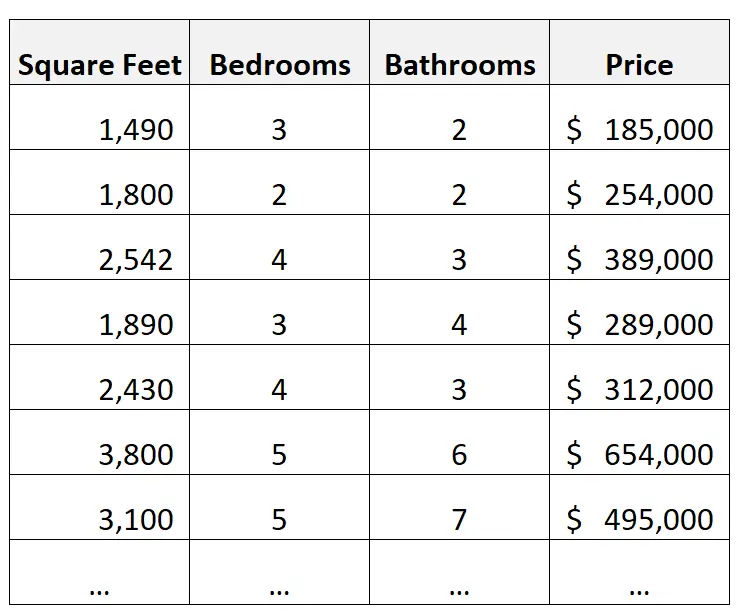
Приклад висновку:

Припустімо, ми створюємо модель множинної лінійної регресії, використовуючи квадратні метри, кількість спалень і кількість ванних кімнат як змінні прогностики та ціну як змінну відповіді.

Тоді ми могли б використати коефіцієнти регресії, щоб зрозуміти середню зміну ціни, пов’язану зі зміною на одну одиницю в кожній із змінних предикторів.

Наприклад, ми могли б зрозуміти, наскільки змінюється ціна (в середньому) з кожною додатковою спальнею, кожною додатковою ванною кімнатою та кожним додатковим квадратним футом.

Приклад передбачення:

Ми могли б побудувати ту саму модель множинної лінійної регресії та використовувати її для прогнозування вартості нового будинку на основі його квадратних метрів, кількості спалень і кількості ванних кімнат.

Наприклад, ми могли б використати модель для прогнозування ціни нового будинку з 3 спальнями, 3 ванними кімнатами та 2000 квадратних футів.

Тоді ми могли б порівняти наш прогноз із фактичною ціною в списку та оцінити, чи виглядає будинок недооціненим чи переоціненим.

Наведені нижче приклади ілюструють різницю між висновком і прогнозом у різних сценаріях:

Приклад 1: Висновок і прогноз у спорті

Припустимо, що ми маємо наступний набір даних, що містить інформацію про професійні баскетбольні команди:

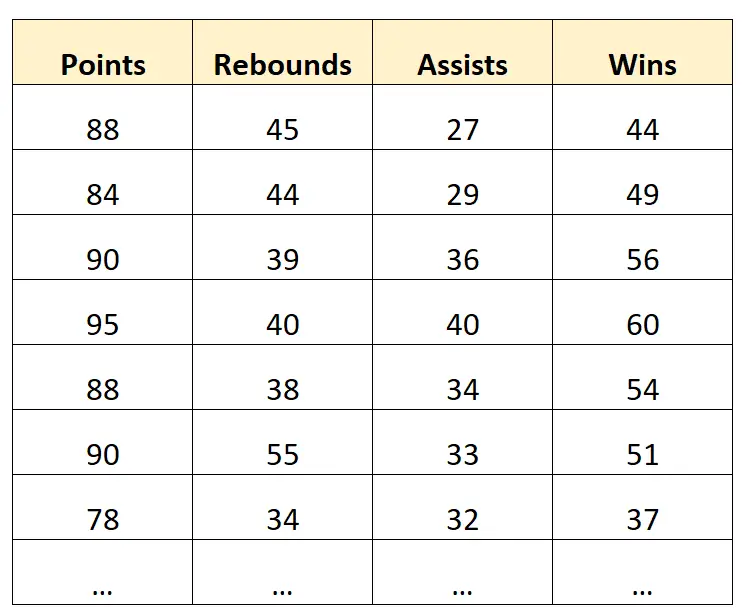
Приклад висновку:

Припустімо, ми створюємо модель множинної лінійної регресії, використовуючи очки, підбирання та результативні передачі як змінні прогнозу та перемоги як змінну відповіді.

Потім ми могли б використовувати модель, щоб зрозуміти, наскільки змінюється кількість перемог (у середньому) з кожним додатковим очком, підбиранням і передачею.

Приклад передбачення:

Ми могли б побудувати ту саму модель множинної лінійної регресії та використовувати її, щоб передбачити, скільки перемог матиме команда на основі її кількості очок, підбирань і передач.

Наприклад, ми могли б використати цю модель, щоб передбачити, скільки перемог матиме команда з 90 очками, 40 підбираннями та 30 передачами.

Приклад 2: Висновок і передбачення в бізнесі

Припустимо, що ми маємо наступний набір даних, що містить інформацію про річний дохід (у мільйонах) різних компаній:

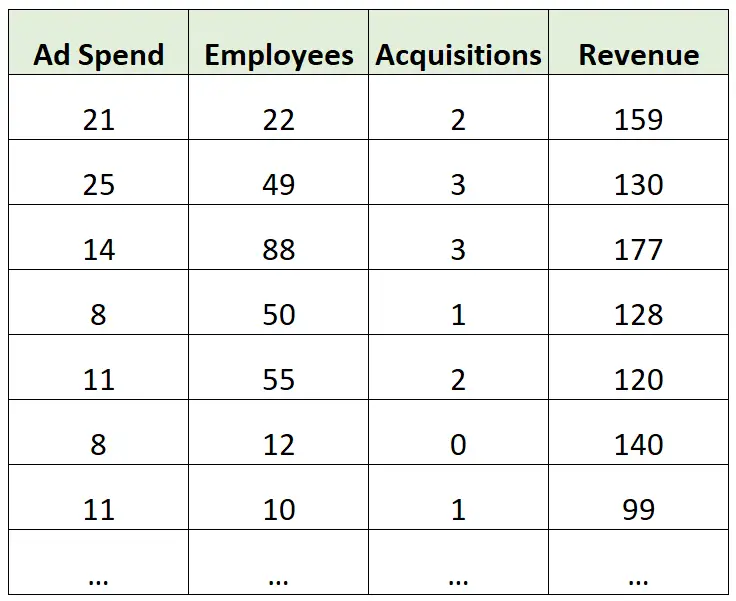
Приклад висновку:

Припустімо, що ми будуємо модель множинної лінійної регресії, використовуючи витрати на рекламу, кількість працівників і загальну кількість придбань як змінні прогнозу та річний дохід як змінну відповіді.

Потім ми могли б використовувати цю модель, щоб зрозуміти, наскільки загальний річний дохід змінюється (в середньому) з кожним додатковим доларом, витраченим на рекламу, кожним додатковим працівником і кожним додатковим придбанням.

Приклад передбачення:

Ми могли б побудувати ту саму модель множинної лінійної регресії та використати її для прогнозування річного доходу компанії на основі її загальних маркетингових витрат, кількості працівників і загальної кількості придбань.

Наприклад, ми могли б використати модель для прогнозування річного доходу компанії, яка витрачає 25 мільйонів доларів на рекламу, має 40 співробітників і здійснила 2 придбання.

Додаткові ресурси

Наступні навчальні посібники надають додаткову інформацію про важливі терміни, які потрібно зрозуміти в статистиці:

Описова чи інференційна статистика: у чому різниця?
Рівні вимірювання: номінальний, порядковий, інтервальний та коефіцієнтний
Якісні та кількісні змінні: у чому різниця?