Коефіцієнт внутрішньокласової кореляції: визначення + приклад

Внутрішньокласовий коефіцієнт кореляції (ICC) використовується для вимірювання надійності балів у дослідженнях, де є два або більше оцінювачів.

Значення ICC може варіюватися від 0 до 1, де 0 означає відсутність надійності серед оцінювачів, а 1 означає повну надійність серед оцінювачів.

Простіше кажучи, ICC використовується для визначення того, чи можуть предмети (або теми) бути достовірно оцінені різними оцінювачами.

Існує кілька різних версій ICC, які можна розрахувати залежно від таких трьох факторів:

• Модель: односторонні випадкові ефекти, двосторонні випадкові ефекти або двосторонні змішані ефекти
• Тип відносин: послідовність або абсолютна згода
• Одиниця: окремий оцінювач або середнє значення оцінювачів

Ось короткий опис трьох різних моделей :

1. Модель односторонніх випадкових ефектів: Ця модель припускає, що кожен предмет оцінюється іншою групою випадково вибраних оцінювачів. У цій моделі джерелом випадкових ефектів вважаються оцінювачі. Ця модель рідко використовується на практиці, оскільки для оцінювання кожного предмета зазвичай використовується та сама група оцінювачів.

2. Двостороння модель випадкових ефектів: ця модель припускає, що групу оцінювачів k випадковим чином вибирають із генеральної сукупності, а потім використовують для оцінювання суб’єктів. За допомогою цієї моделі оцінювачі та суб’єкти вважаються джерелами випадкових ефектів. Ця модель часто використовується, коли ми хочемо узагальнити наші результати для оцінювачів, подібних до тих, що використовуються в дослідженні.

3. Двостороння модель змішаних ефектів: ця модель також припускає, що групу оцінювачів k випадковим чином вибирають із сукупності, а потім використовують для оцінювання суб’єктів. Однак ця модель припускає, що група оцінювачів, яку ми обрали, є єдиними оцінювачами, що представляють інтерес, тобто ми не хочемо узагальнювати наші результати на інших оцінювачів, які також можуть мати подібні характеристики з оцінювачами, використаними в дослідженні.

Ось короткий опис двох різних типів відносин, які ми можемо захотіти виміряти:

1. Узгодженість: нас цікавлять систематичні відмінності між оцінками суддів (наприклад, чи оцінювали судді схожі теми як низькі та високі?)

2. Абсолютна згода: нас цікавить абсолютна різниця між оцінками суддів (наприклад, яка абсолютна різниця між оцінками судді А та судді Б?)

Ось короткий опис двох різних одиниць , які можуть нас зацікавити:

1. Один рецензент: ми хочемо використовувати лише оцінки одного рецензента як основу для вимірювання.

2. Середнє оцінювальне значення: ми хочемо використовувати середнє значення всіх оцінок суддів як основу для вимірювання.

Примітка. Якщо ви хочете виміряти рівень узгодженості між двома оцінювачами, які пропускають кожну позицію щодо дихотомічного результату , замість цього слід використовувати Каппа Коена .

Як інтерпретувати внутрішньокласовий коефіцієнт кореляції

Ось як інтерпретувати значення внутрішньокласового коефіцієнта кореляції згідно з Ку та Лі :

• Менше 0,50: низька надійність
• Між 0,5 і 0,75: помірна надійність
• Між 0,75 і 0,9: хороша надійність
• Більше 0,9: відмінна надійність

У наступному прикладі показано, як на практиці розрахувати внутрішньокласовий коефіцієнт кореляції.

Приклад: Розрахунок внутрішньокласового коефіцієнта кореляції

Припустімо, чотирьох різних суддів просять оцінити якість 10 різних вступних іспитів до коледжу. Результати наведені нижче:

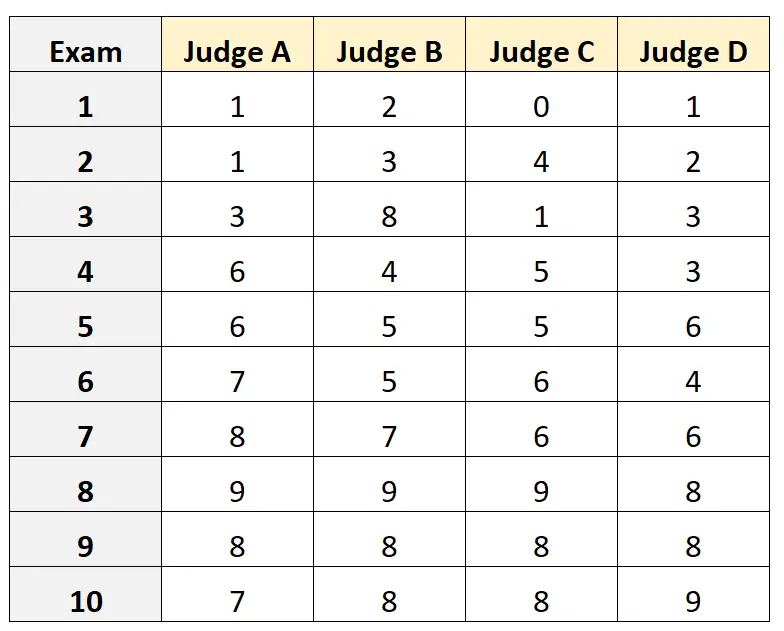
Припустімо, що чотири судді були випадковим чином обрані з групи кваліфікованих суддів для вступного іспиту, і ми хотіли виміряти абсолютну згоду між суддями, і ми хотіли використовувати бали з точки зору лише одного оцінювача як основу нашого вимірювання.

Ми можемо використати наступний код у R, щоб відповідати двосторонній моделі випадкових ефектів , використовуючи абсолютну згоду як відношення між оцінювачами та використовуючи одну одиницю як одиницю інтересу:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

Коефіцієнт внутрішньокласової кореляції (ICC) склав 0,782 .

Базуючись на емпіричних правилах тлумачення ICC, ми дійшли висновку, що ICC 0,782 вказує на те, що іспити можуть бути оцінені з «хорошою» надійністю різними оцінювачами.

Додаткові ресурси

Наступні навчальні посібники містять детальні пояснення щодо того, як обчислити ICC у різних статистичних програмах:

Як розрахувати внутрішньокласовий коефіцієнт кореляції в Excel
Як розрахувати внутрішньокласовий коефіцієнт кореляції в R
Як обчислити внутрішньокласовий коефіцієнт кореляції в Python