Гамма-розподіл

за Редакція 3 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке гамма-розподіл і для чого він використовується. Таким чином, ви знайдете визначення гамма-розподілу, його властивості та те, як виглядає його графічне представлення.

Що таке гамма-розподіл?

Гамма-розподіл — це безперервний розподіл ймовірностей, який визначається двома характерними параметрами, α і λ. Іншими словами, гамма-розподіл залежить від значення двох його параметрів: α — параметр форми та λ — параметр масштабу.

Символом гамма-розподілу є велика грецька літера Γ. Отже, якщо випадкова величина відповідає гамма-розподілу, вона записується так:

$X\sim \Gamma(\alpha,\lambda)$

Гамма-розподіл також можна параметризувати за допомогою параметра форми k = α та параметра оберненого масштабу θ = 1/λ. У всіх випадках два параметри, які визначають гамма-розподіл, є позитивними дійсними числами.

Як правило, гамма-розподіл використовується для моделювання наборів даних зі зміщенням управо, щоб у лівій частині графіка була більша концентрація даних. Наприклад, гамма-розподіл використовується для моделювання надійності електричних компонентів.

Діаграма гамма-розподілу

Графік гамма-розподілу залежить від значень його характерних параметрів. Нижче ви можете побачити, як змінюється функція щільності гамма-розподілу залежно від параметра форми та параметра масштабу.

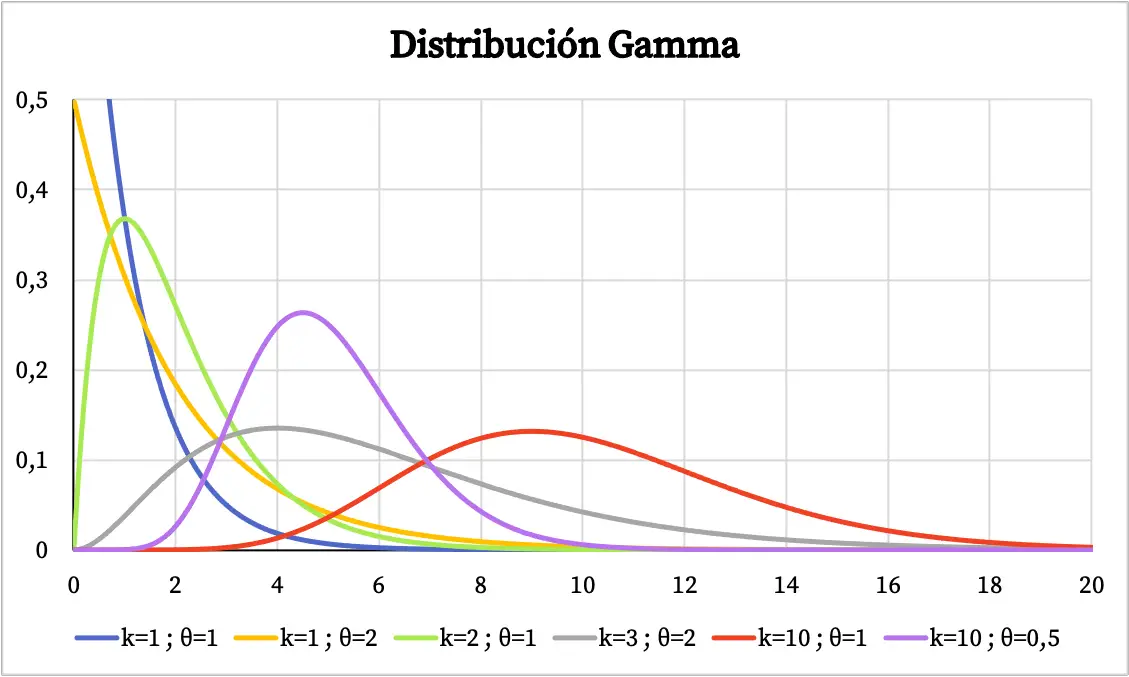
З іншого боку, ви можете побачити графік кумулятивної функції ймовірності гамма-розподілу нижче:

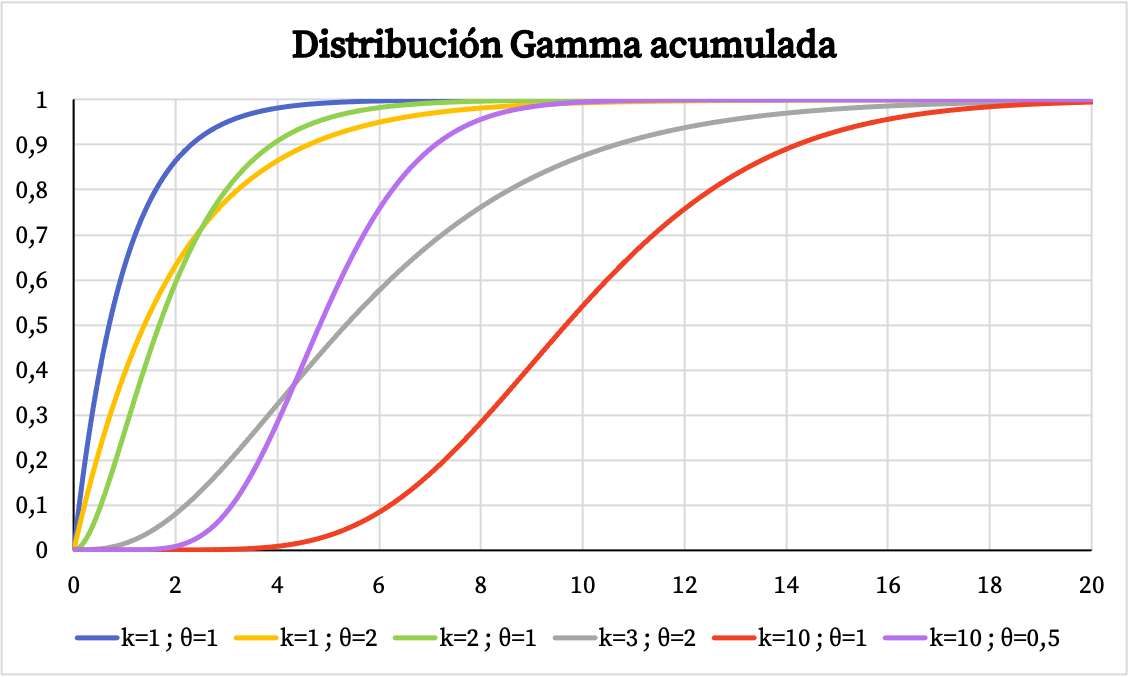
графік кумулятивної функції ймовірності розподілу Гамма

Характеристика гамма-розподілу

Потім ми побачимо, якими є характеристики гамма-розподілу.

Графік гамма-розподілу повністю визначається двома характерними параметрами: α – параметр форми та λ – параметр масштабу.

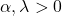
$\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul> <li> Область гамма-розподілу складається тільки з додатних чисел.</li> </ul> <p class=$ $x\in (0,+\infty)$

Середнє гамма-розподілу дорівнює відношенню між параметром форми та параметром масштабу, тобто α/λ.

$E[X]=\cfrac{\alpha}{\lambda}$

Дисперсія гамма-розподілу еквівалентна параметру форми, поділеному на квадрат параметра масштабу.

$Var(X)=\cfrac{\alpha}{\lambda^2}$

Для значень α менше 1 мода дорівнює 0. Але якщо α дорівнює або більше 1, моду гамма-розподілу можна розрахувати за такою формулою:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

Формула функції щільності гамма-розподілу:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

Де Γ — гамма-функція, яка визначається як:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

Формула кумулятивного розподілу випадкової величини, визначеної гамма-розподілом, має такий вигляд:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

Якщо параметр форми α дорівнює 1, то гамма-розподіл еквівалентний експоненціальному розподілу з тим самим параметром масштабу λ.

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

Коли параметр масштабу λ є середнім, тоді гамма-розподіл є окремим випадком розподілу хі-квадрат .

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке гамма-розподіл?

Діаграма гамма-розподілу

Характеристика гамма-розподілу

Про автора

Редакція

Додати коментар