Введення в геометричний розподіл

Геометричний розподіл описує ймовірність зазнати певної кількості невдач, перш ніж відчути перший успіх у серії випробувань Бернуллі.

Випробування Бернуллі — це експеримент лише з двома можливими результатами — «успіх» або «невдача», і ймовірність успіху є однаковою кожного разу, коли експеримент проводиться.

Прикладом есе Бернуллі є підкидання монети. Монета може впасти лише на дві голови (ми можемо назвати орли «ударом», а решка — «провалом»), а ймовірність успіху кожного підкидання становить 0,5, якщо монета чесна.

Якщо випадкова величина X відповідає геометричному розподілу, то ймовірність зазнати k невдач до першого успіху можна знайти за такою формулою:

P(X=k) = (1-p) ^kp

золото:

• k: кількість невдач перед першим успіхом
• p: ймовірність успіху в кожному випробуванні

Наприклад, скажімо, ми хочемо знати, скільки разів нам потрібно підкинути чесну монету, поки вона не випаде орел. Ми можемо використовувати наведену вище формулу, щоб визначити ймовірність виникнення 0, 1, 2, 3 збоїв тощо. до того, як монета впаде на голови:

Примітка: монета може зазнати 0 «провалів», якщо під час першого підкидання випаде орел.

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-0,5) ¹ (0,5) = 0,25

P(X=2) = (1-0,5) ² (0,5) = 0,125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Ми можемо обчислити ймовірність будь-якої кількості підкинутих монет до нескінченності. Потім ми створюємо просту гістограму, щоб візуалізувати цей розподіл ймовірностей:

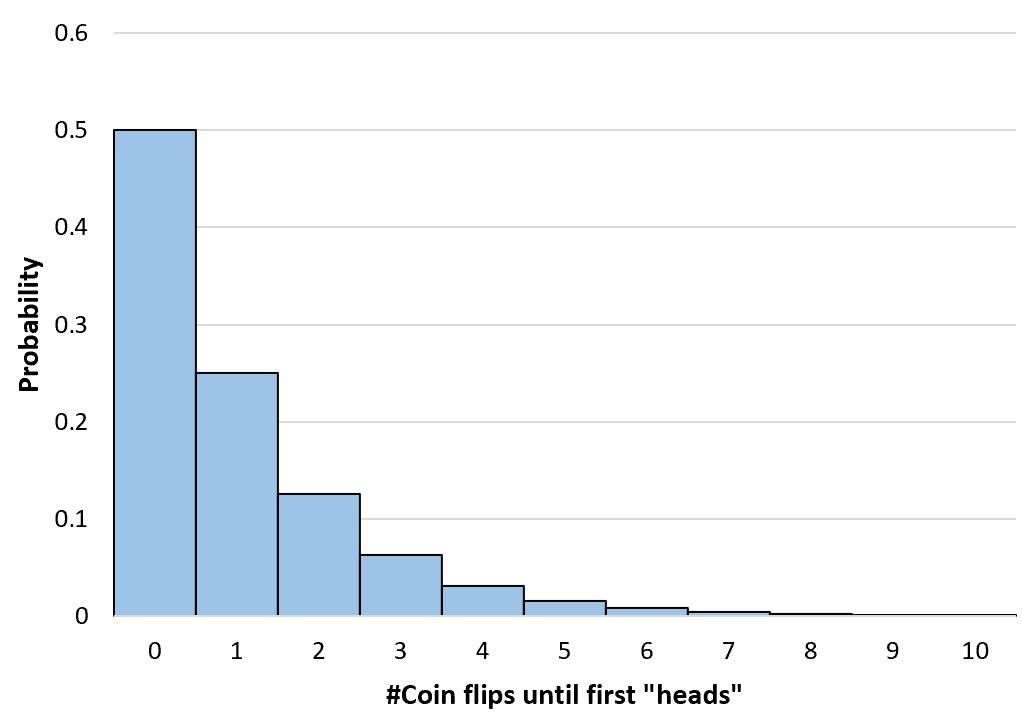
Обчислення кумулятивних геометричних ймовірностей

Кумулятивну ймовірність того, що ми зазнаємо k або менше невдач до першого успіху, можна знайти за такою формулою:

P(X≤k) = 1 – (1-p) ^k+1

золото:

• k: кількість невдач перед першим успіхом
• p: ймовірність успіху в кожному випробуванні

Наприклад, припустімо, що ми хочемо знати ймовірність того, що буде потрібно три або менше «промахів», перш ніж монета нарешті приземлиться на головах. Щоб обчислити цю ймовірність, ми використаємо таку формулу:

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Ми можемо обчислити кожну сукупну ймовірність за аналогічною формулою:

P(X≤0) = 1 – (1-,5) ⁰⁺¹ = 0,5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Ми можемо обчислити ці кумулятивні ймовірності для будь-якої кількості підкидань монети до нескінченності. Потім ми можемо створити гістограму для візуалізації цього кумулятивного розподілу ймовірностей:

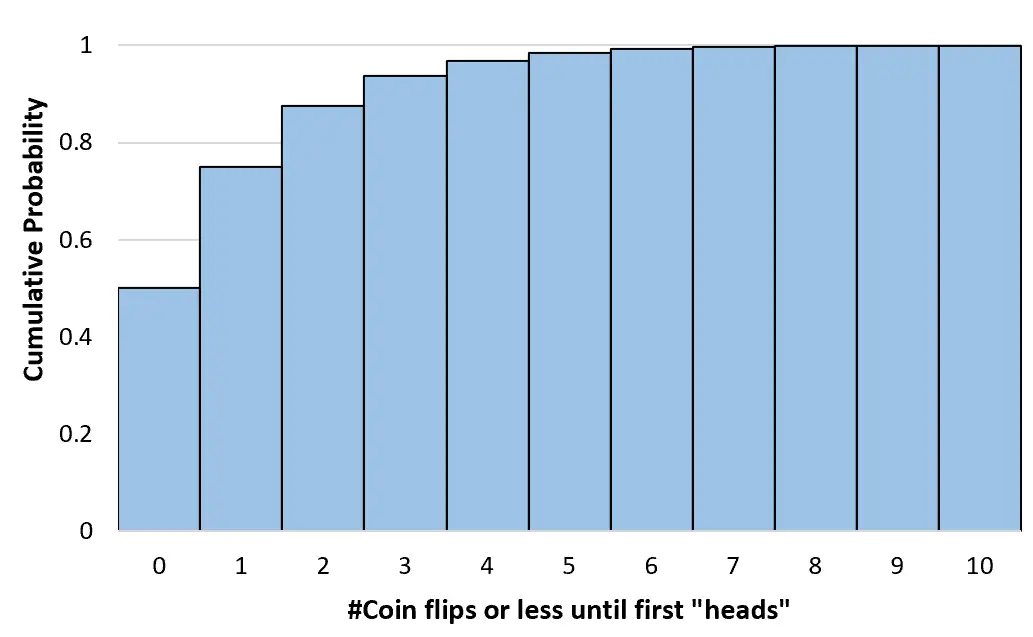
Властивості геометричного розподілу

Геометричний розподіл має такі властивості:

Середнє значення розподілу дорівнює (1-p) / p .

Дисперсія розподілу дорівнює (1-p)/p ² .

Наприклад:

Середня кількість разів, коли ми очікуємо, що монета впаде головою перед тим, як приземлиться хвою, буде (1-p) / p = (1-.5) / .5 = 1 .

Дисперсія кількості кидків, доки він не впаде на голову, буде (1-p)/ ^p2 =(1-.5)/. ⁵² = 2 .

Практичні задачі геометричного розподілу

Використовуйте наведені нижче практичні завдання, щоб перевірити свої знання про геометричний розподіл.

Примітка. Щоб обчислити відповіді на ці запитання, ми використаємо калькулятор геометричного розподілу .

Проблема 1

Запитання: Дослідник чекає біля бібліотеки, щоб запитати людей, чи підтримують вони певний закон. Імовірність того, що дана особа підтримує закон, становить p = 0,2. Яка ймовірність того, що четверта особа, з якою розмовляє дослідник, першою підтримає закон?

Відповідь: кількість «невдач» до першого успіху, тобто кількість людей, які не підтримують закон, доки його не підтримає перша особа, дорівнює 3. Отже, при використанні калькулятора геометричного розподілу з p = 0,2 і x = 3 невдачі, знаходимо, що P(X=3) = 0,10240 .

Проблема 2

Запитання: Дослідник чекає біля бібліотеки, щоб запитати людей, чи підтримують вони певний закон. Імовірність того, що дана особа підтримує закон, становить p = 0,2. Яка ймовірність того, що досліднику доведеться поговорити з більш ніж чотирма людьми, щоб знайти когось, хто підтримує закон?

Відповідь: Використовуючи калькулятор геометричного розподілу з p =0,2 і x = 4 невдачі, ми знаходимо, що P(X>4) = 0,32768 .

Проблема 3

Запитання: Дослідник чекає біля бібліотеки, щоб запитати людей, чи підтримують вони певний закон. Імовірність того, що дана особа підтримує закон, становить p = 0,2. З якою очікуваною кількістю людей досліднику доведеться поговорити, поки вона не знайде когось, хто підтримує закон?

Відповідь: Згадайте, що середнє геометричного розподілу дорівнює (1-p) / p . У цій ситуації середнє значення буде (1-,2) / ,2 = 4 .