Як використовувати геометричний розподіл в excel

Геометричний розподіл описує ймовірність зазнати певної кількості невдач, перш ніж відчути перший успіх у серії випробувань Бернуллі.

Випробування Бернуллі — це експеримент лише з двома можливими результатами — «успіх» або «невдача», і ймовірність успіху є однаковою кожного разу, коли експеримент проводиться.

Прикладом есе Бернуллі є підкидання монети. Монета може впасти лише на дві голови (ми можемо назвати орли «ударом», а решка — «провалом»), а ймовірність успіху кожного підкидання становить 0,5, якщо монета чесна.

Якщо випадкова величина X відповідає геометричному розподілу, то ймовірність зазнати k невдач до першого успіху можна знайти за такою формулою:

P(X=k) = (1-p) ^kp

золото:

• k: кількість невдач перед першим успіхом
• p: ймовірність успіху в кожному випробуванні

У наведених нижче прикладах показано, як обчислити ймовірності, пов’язані з геометричним розподілом у Excel.

Приклад 1: підкинути монету

Припустімо, що ми кидаємо монету й хочемо знати ймовірність того, що знадобляться рівно три «промахи», перш ніж монета нарешті випаде головою.

Щоб обчислити цю ймовірність, ми використаємо таку формулу:

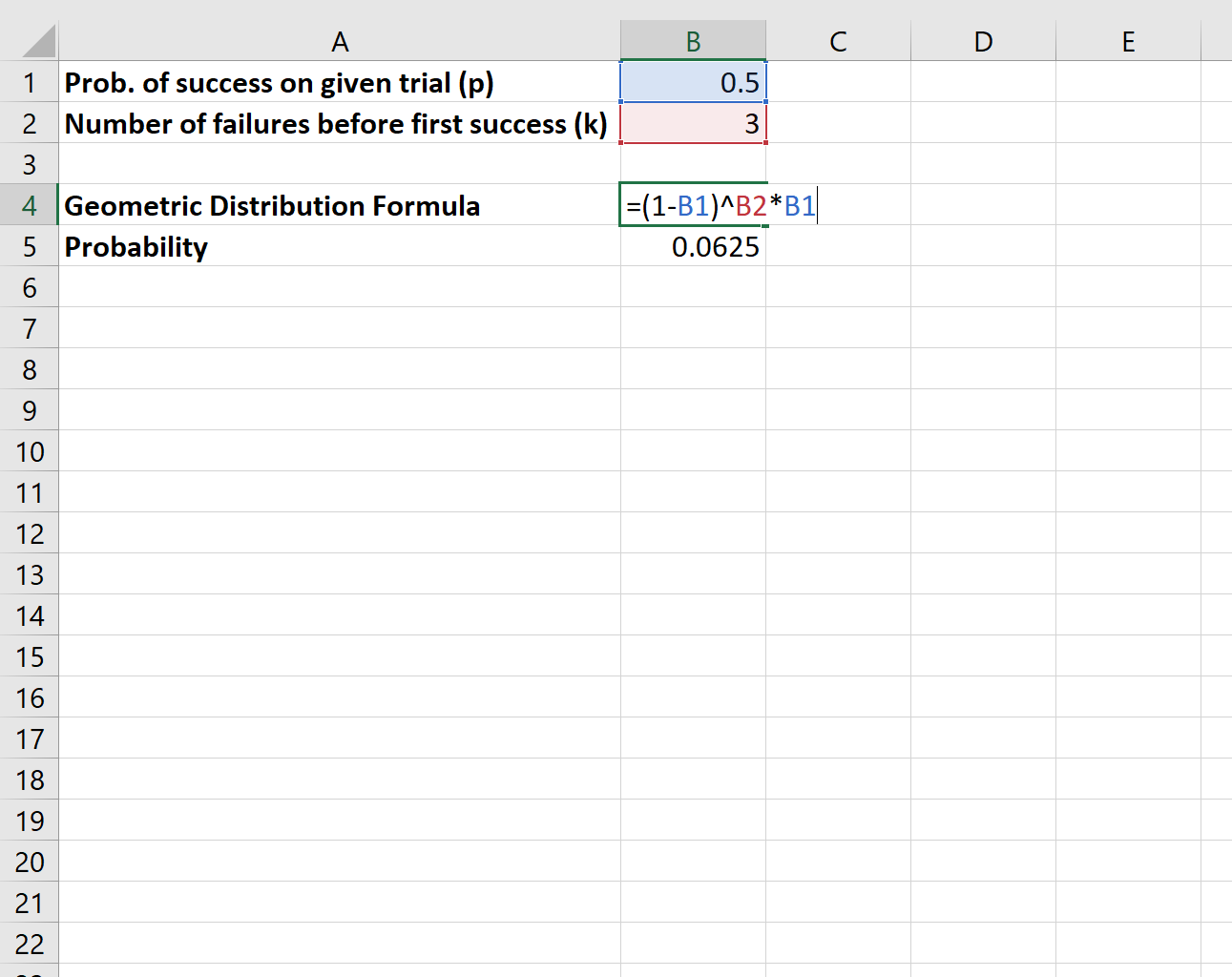
Імовірність того, що ми зазнаємо трьох «промахів», поки монета нарешті не випаде вгору, становить 0,0625 .

Приклад 2: Штрафний кидок

Припустимо, певний баскетболіст виконує 60% своїх штрафних кидків. Яка ймовірність того, що гравець промахнеться чотирма штрафними кидками, поки він нарешті не зробить один?

Щоб обчислити цю ймовірність, ми використаємо таку формулу:

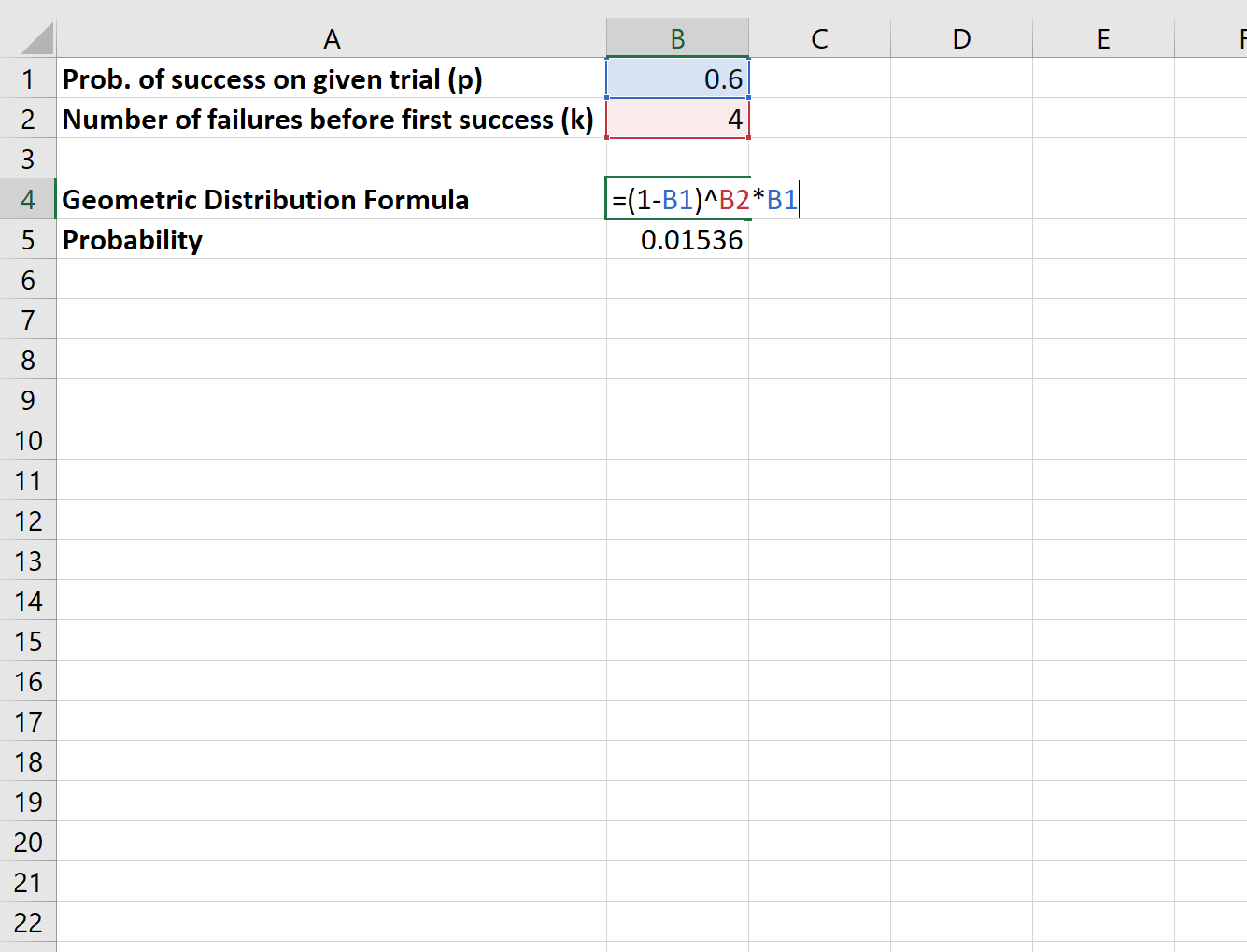
Імовірність того, що гравець промахнеться чотирма штрафними кидками, поки він нарешті не зробить один, становить 0,01536 .

Приклад 3: Підтримка закону

Припустімо, що дослідник чекає біля бібліотеки, щоб запитати людей, чи підтримують вони певний закон. Імовірність того, що дана особа підтримує закон, становить p = 0,2. Яка ймовірність того, що четверта особа, з якою розмовляє дослідник, першою підтримає закон?

Щоб обчислити цю ймовірність, ми використаємо таку формулу:

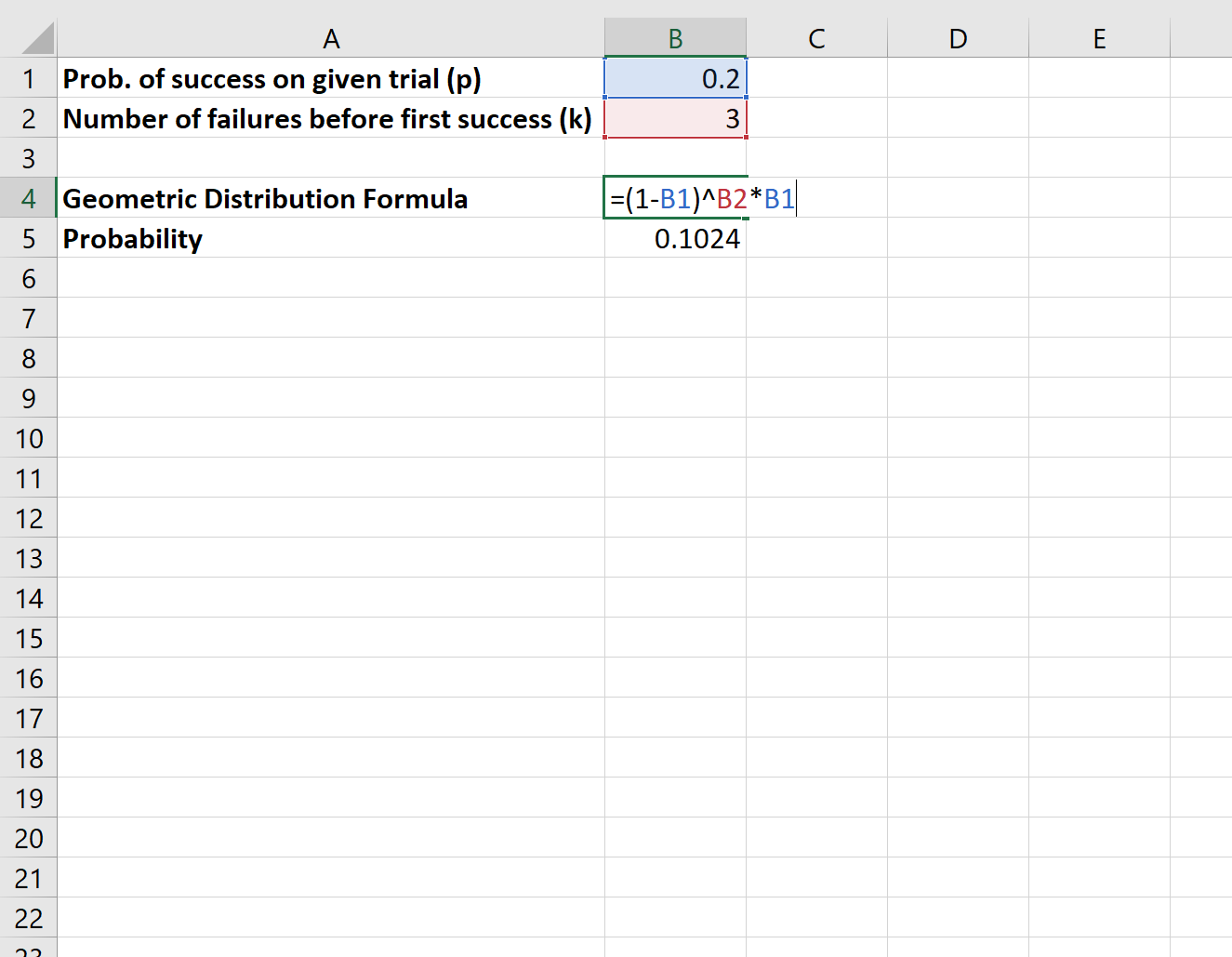
Імовірність того, що четверта людина, з якою розмовляє дослідник, першою підтримає закон, становить 0,1024 .

Додаткові ресурси

Введення в геометричний розподіл
Геометричний калькулятор розподілу
5 конкретних прикладів геометричного розподілу