Як створити часткові залишкові ділянки в r

Множинна лінійна регресія – це статистичний метод, який ми можемо використовувати для розуміння зв’язку між декількома змінними предикторів і змінною відповіді .

Однак одне з ключових припущень множинної лінійної регресії полягає в тому, що існує лінійний зв’язок між кожною змінною предиктора та змінною відповіді.

Якщо це припущення не виконується, то результати регресійної моделі можуть бути ненадійними.

Одним із способів перевірити це припущення є створення графіка часткових залишків , який відображає залишки змінної предиктора відносно змінної відповіді.

У наступному прикладі показано, як створити графіки часткових залишків для регресійної моделі в R.

Приклад: як створити часткові залишкові ділянки в R

Припустімо, що ми підганяємо модель регресії з трьома змінними предикторів у R:

 #make this example reproducible
set. seeds (0)

#define response variable
y <- c(1:1000)

#define three predictor variables
x1 <- c(1:1000)*runif(n=1000)
x2 <- (c(1:1000)*rnorm(n=1000))^2
x3 <- (c(1:1000)*rnorm(n=1000))^3

#fit multiple linear regression model
model <- lm(y~x1+x2+x3))

Ми можемо використовувати функцію crPlots() із пакета автомобіля в R, щоб створити часткові залишкові графіки для кожної змінної предиктора в моделі:

 library (car)

#create partial residual plots
crPlots(model)

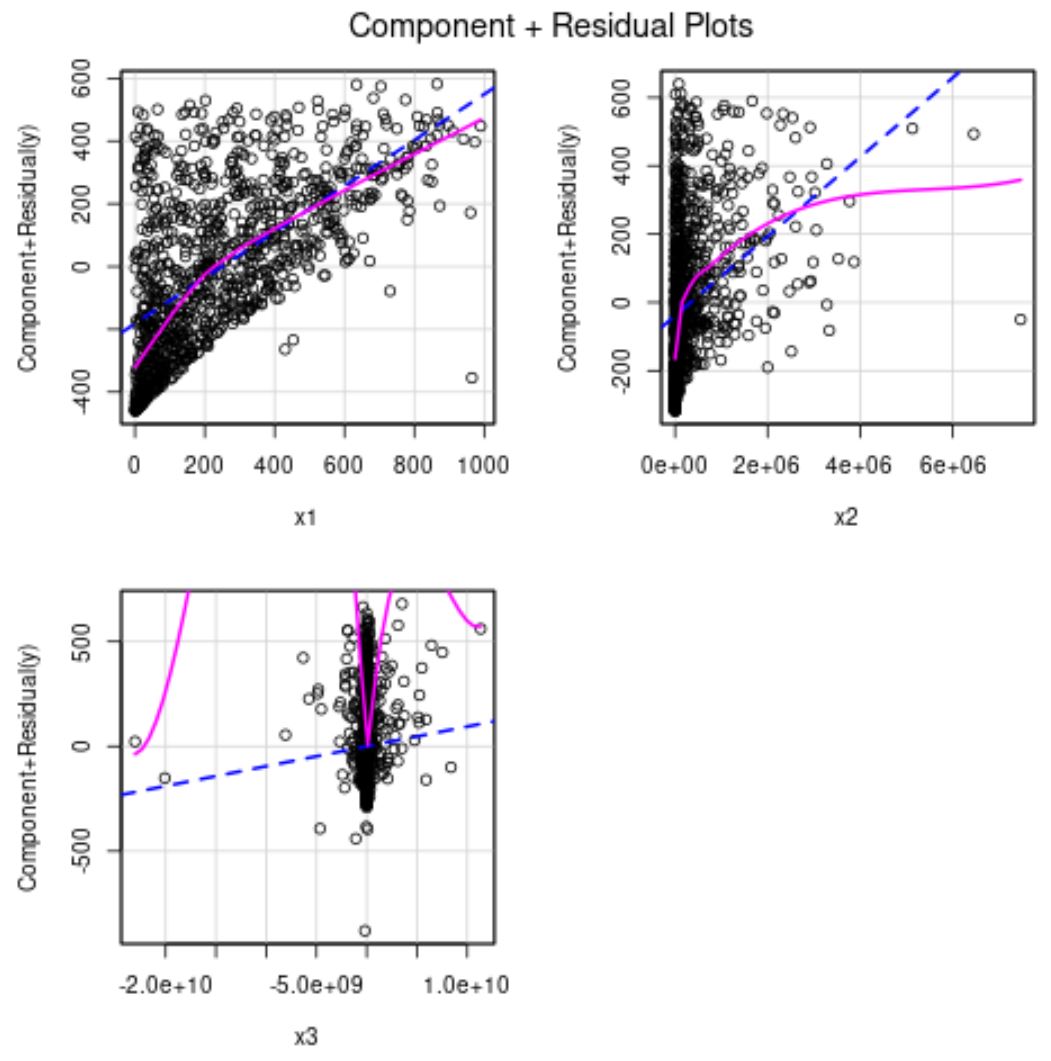
Синя лінія показує очікувані залишки, якщо зв’язок між предиктором і змінною відповіді був лінійним. Рожева лінія показує фактичні залишки.

Якщо дві лінії значно відрізняються, це вказує на нелінійний зв’язок.

З наведених вище графіків ми бачимо, що залишки для x2 і x3 виглядають нелінійними.

Це порушує припущення про лінійність множинної лінійної регресії. Один із способів розв’язати цю проблему — використати перетворення квадратного або кубічного кореня для змінних предиктора:

 library (car)

#fit new model with transformed predictor variables
model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3)))

#create partial residual plots for new model
crPlots(model_transformed)

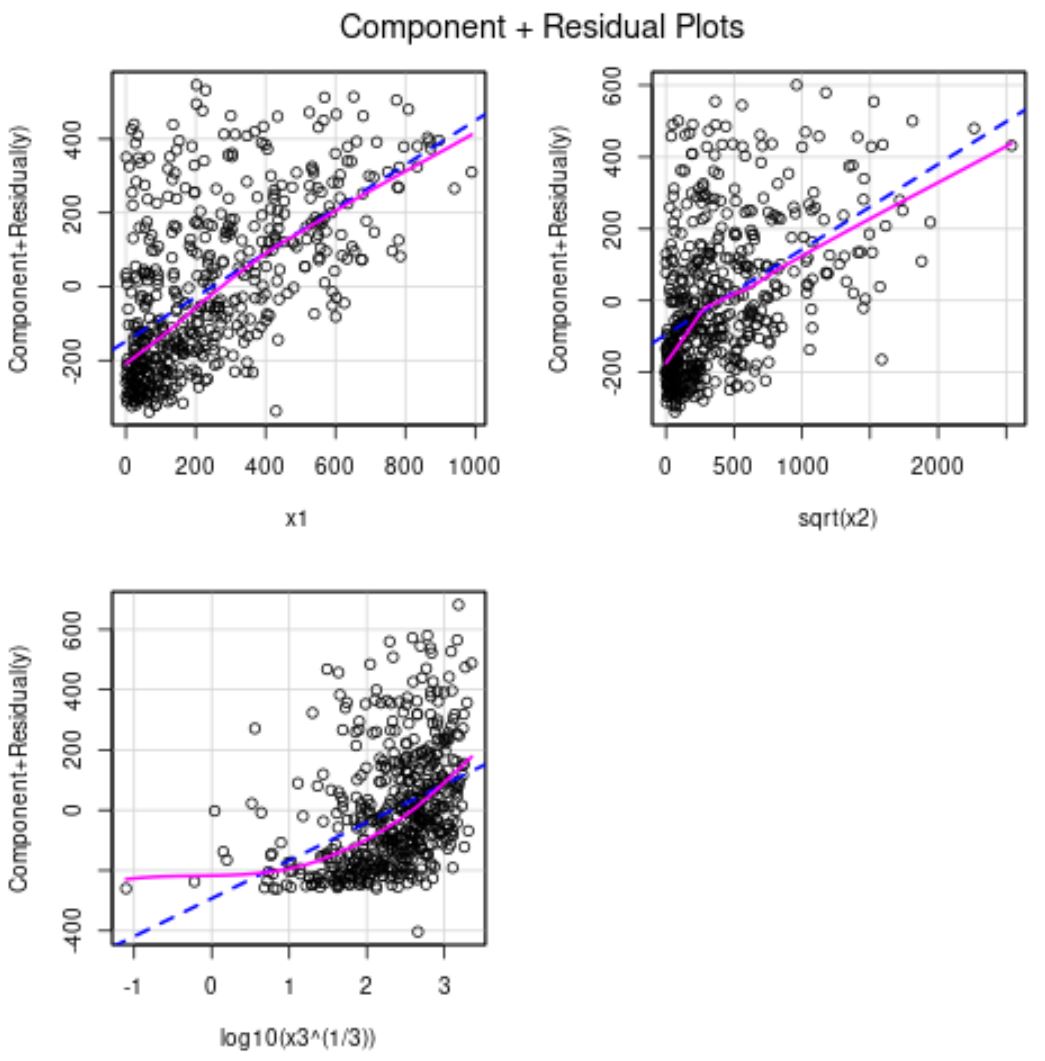
З графіків часткових залишків ми бачимо, що x2 тепер має більш лінійний зв’язок зі змінною відповіді.

Змінна предиктора x3 все ще дещо нелінійна, тому ми можемо вирішити спробувати інше перетворення або, можливо, взагалі видалити змінну з моделі.

Додаткові ресурси

У наступних посібниках пояснюється, як створити інші типові діаграми в R:

Як створити діаграми діагностики в R
Як створити діаграму масштабу та розташування в R
Як створити ділянку залишків у R