Гіпергеометричний розподіл

за Редакція 6 Серпня, 2023 Ймовірність 0 коментарів

У цій статті ми пояснюємо, що таке гіпергеометричний розподіл і як обчислюється ймовірність із цим типом розподілу. Ви знайдете онлайн формулу для гіпергеометричного розподілу, його характеристики, а також калькулятор для обчислення ймовірності гіпергеометричного розподілу.

Що таке гіпергеометричний розподіл?

Гіпергеометричний розподіл — це розподіл ймовірностей, який описує кількість успішних випадків у випадковому вилученні без заміни n елементів із сукупності.

Тобто гіпергеометричний розподіл використовується для обчислення ймовірності отримання x успіхів при вилученні n елементів із сукупності без заміни жодного з них.

Гіпергеометричний розподіл має три параметри:

N : кількість елементів у сукупності (N = 0, 1, 2,…).
K : максимальна кількість успішних випадків (K = 0, 1, 2,…,N). Оскільки в гіпергеометричному розподілі елемент можна вважати лише «успішним» або «невдалим», NK — це максимальна кількість випадків відмови.
n : це кількість виконаних вибірок без заміни.

$X \sim HG(N,K,n)$

Наприклад, дискретна випадкова величина X, яка має гіпергеометричний розподіл з параметрами N=8, K=5 і n=3, визначається наступним чином:

$X \sim HG(8,5,3)$

Гіпергеометрична формула розподілу

Формула для гіпергеометричного розподілу є добутком комбінаторного числа K на x на комбінаторне число NK на nx , поділеного на комбінаторне число N на n .

Де N — розмір популяції, K — загальна кількість сприятливих випадків, n — кількість вилучень без заміни, а x — кількість сприятливих випадків, для яких необхідно розрахувати ймовірність появи.

👉 Ви можете скористатися калькулятором нижче, щоб обчислити ймовірність події змінної, яка відповідає гіпергеометричному розподілу.

Приклад гіпергеометричного розподілу

Після того, як ми ознайомилися з визначенням і формулою гіпергеометричного розподілу, ми крок за кроком розв’яжемо приклад, щоб ви знали, як обчислити ймовірність гіпергеометричного розподілу.

У мішок поклали 20 синіх кульок і 30 червоних кульок, тобто всього в мішку 50 кульок. Якщо ми витягнемо 12 куль, не замінивши жодної, знайдіть ймовірність витягнути 4 сині кульки.

Перше, що нам потрібно зробити, щоб вирішити вправу, це визначити параметри гіпергеометричного розподілу. У цьому випадку загальна кількість елементів у популяції становить 50 ( N =50), максимальна кількість сприятливих випадків становить 20 ( K =20), витягується 12 куль ( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

Ми хочемо обчислити ймовірність вилучення 4 синіх куль ( x =4), тому ми застосовуємо формулу гіпергеометричного розподілу, замінюємо змінні відповідними значеннями та виконуємо обчислення:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Калькулятор гіпергеометричного розподілу

Введіть параметри гіпергеометричного розподілу в наступний онлайн-калькулятор, щоб розрахувати ймовірність настання потрібної події.

Пам’ятайте, що N – це розмір сукупності, K – загальна кількість сприятливих випадків, n – розмір вибірки, а x – це значення, для якого ми хочемо знайти ймовірність того, що це станеться.

Характеристика гіпергеометричного розподілу

Гіпергеометричний розподіл має такі властивості:

Очікуване значення гіпергеометричного розподілу дорівнює кількості елементів у вибірці, помноженій на загальну кількість сприятливих випадків, поділену на кількість елементів у сукупності.

$E[X]=\cfrac{n\cdot K}{N}$

Мода гіпергеометричного розподілу – це значення, округлене в меншу сторону від добутку n+1 , помноженого на K+1 , поділеного на N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

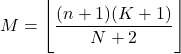
Дисперсію гіпергеометричного розподілу можна отримати за допомогою наступного виразу:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

Твірна функція моменту гіпергеометричного розподілу має такий вигляд:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

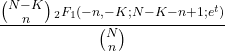
Характерна функція гіпергеометричного розподілу така:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

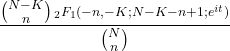
Імовірність появи заданої кількості подій можна обчислити з ймовірності попереднього числа за допомогою рекурсивного для гіпергеометричного розподілу:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Гіпергеометричний розподіл і біноміальний розподіл

Різниця між гіпергеометричним розподілом і біноміальним розподілом полягає в заміні. Гіпергеометричний розподіл використовується, коли пошуки не замінюються, однак у біноміальному розподілі пошуки замінюються.

Наприклад, якщо ми випадково беремо п’ять карт у колоді й хочемо обчислити ймовірність отримання певної карти, якщо ми не замінимо кожну взяту картку, ми повинні використовувати гіпергеометричний розподіл, щоб виконати обчислення. Але якщо, виймаючи картку, ми повертаємо її перед наступним вилученням, тоді для обчислення ймовірності потрібно використовувати біноміальний розподіл.

Коли число N велике, відношення n/N мало, а кількість бажаних сприятливих випадків дуже мала, ми можемо використовувати гіпергеометричний розподіл як наближення біноміального розподілу. Однак я не рекомендую цього, тому що результат не буде настільки надійним, і, крім того, легше розрахувати ймовірності за біноміальним законом, ніж за гіпергеометричним законом.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше