П'ять гіпотез кореляції пірсона
Коефіцієнт кореляції Пірсона (також відомий як «коефіцієнт кореляції продукт-момент») вимірює лінійний зв’язок між двома змінними.
Він завжди приймає значення від -1 до 1, де:
- -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
- 0 означає відсутність лінійної кореляції між двома змінними
- 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними
Однак, перш ніж обчислювати коефіцієнт кореляції Пірсона між двома змінними, ми повинні переконатися, що виконуються п’ять припущень:
1. Рівень вимірювання: обидві змінні слід вимірювати на рівні інтервалу або співвідношення .
2. Лінійний зв’язок: між двома змінними має бути лінійний зв’язок.
3. Нормальність: обидві змінні повинні мати приблизно нормальний розподіл.
4. Пов’язані пари: кожне спостереження в наборі даних повинно мати пару значень.
5. Відсутність викидів: у наборі даних не повинно бути екстремальних викидів.
У цій статті ми пояснюємо кожне припущення, а також пояснюємо, як визначити, чи виконується це припущення.
Гіпотеза 1: Рівень вимірювання
Щоб обчислити коефіцієнт кореляції Пірсона між двома змінними, обидві змінні повинні бути виміряні на рівні інтервалу або співвідношення .
Наступна графіка надає швидке пояснення чотирьох рівнів, на яких можна вимірювати змінні:
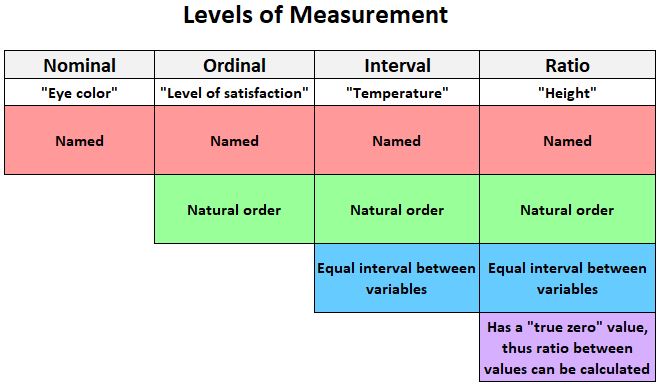
Ось кілька прикладів змінних, які можна виміряти за інтервальною шкалою:
- Температура: вимірюється у градусах Фаренгейта або Цельсія
- Кредитні бали: вимірюються від 300 до 850
- Оцінки SAT: вимірюються від 400 до 1600
Ось кілька прикладів змінних, які можна виміряти за шкалою співвідношення :
- Зріст: вимірюється в сантиметрах, дюймах, футах тощо.
- Вага: вимірюється в кілограмах, фунтах тощо.
- Довжина: вимірюється в сантиметрах, дюймах, футах тощо.
Якщо змінні вимірюються на порядковому рівні, то вам потрібно обчислити коефіцієнт кореляції Спірмена між ними.
Пов’язані: Рівні вимірювання: номінальний, порядковий, інтервальний і коефіцієнт
Гіпотеза 2: Лінійний зв’язок
Щоб обчислити коефіцієнт кореляції Пірсона між двома змінними, між двома змінними має бути лінійна залежність.
Найпростіший спосіб перевірити цю гіпотезу — просто створити діаграму розсіювання двох змінних. Якщо точки на графіку йдуть приблизно по прямій лінії, то існує лінійна залежність:
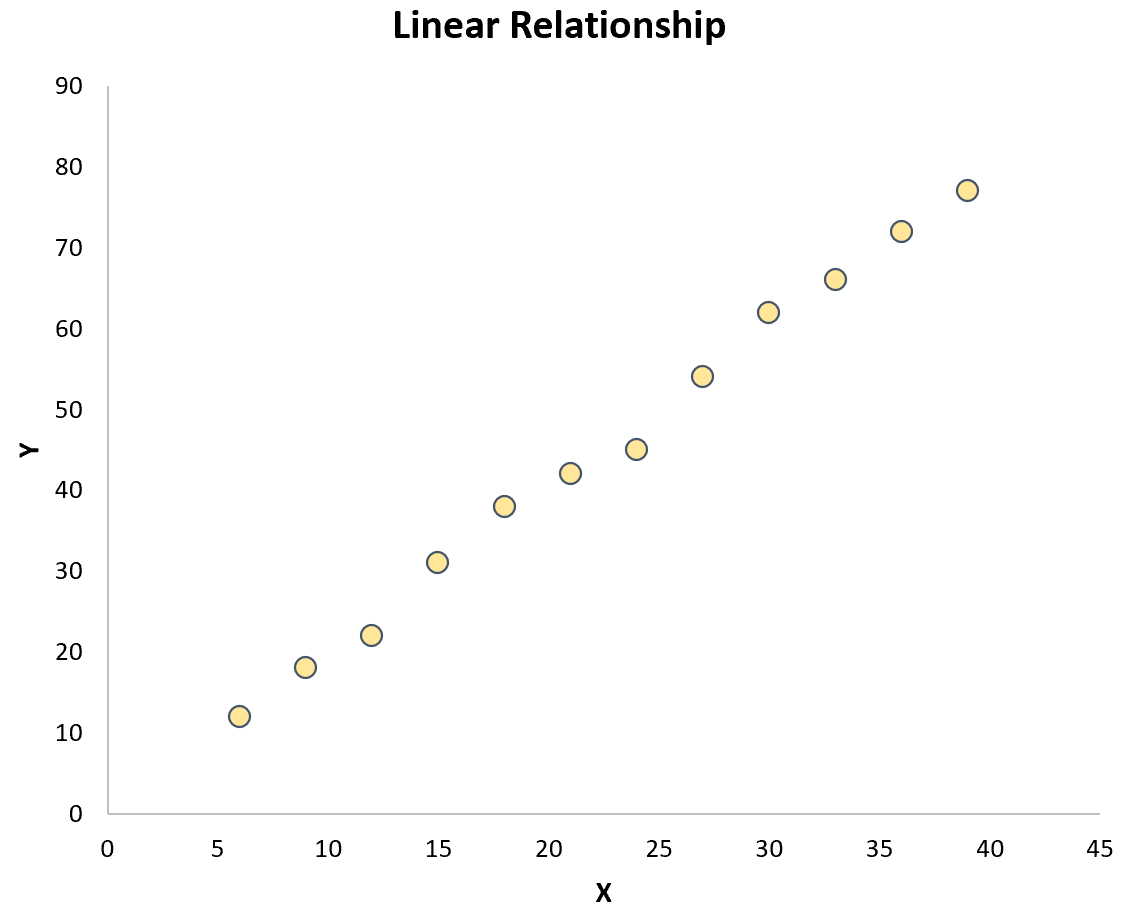
Однак, якщо точки випадково розкидані по графіку або мають якийсь інший тип зв’язку (наприклад, квадратичного), то між змінними не існує лінійного зв’язку:
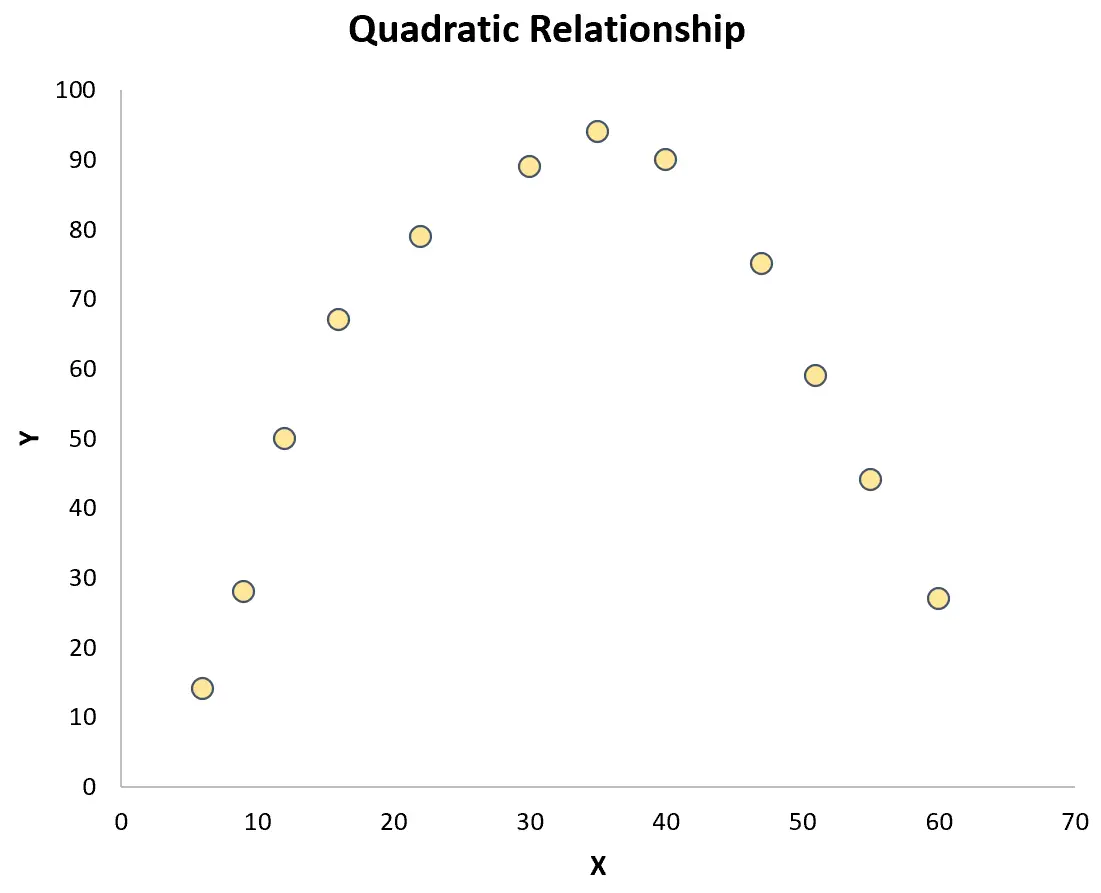
У цьому випадку коефіцієнт кореляції Пірсона не буде адекватно відображати зв’язок між змінними.
Гіпотеза 3: нормальність
Коефіцієнт кореляції Пірсона також передбачає, що дві змінні розподілені приблизно нормально .
Ви можете перевірити це припущення візуально, створивши гістограму або графік QQ для кожної змінної.
1. Гістограма
Якщо гістограма набору даних має приблизно форму дзвона, швидше за все, дані розподілені нормально.

2. QQLand
Діаграма QQ, скорочення від «квантиль-квантиль», — це тип графіка, який відображає теоретичні квантилі вздовж осі абсцис (тобто де були б ваші дані, якби вони відповідали нормальному розподілу) і квантилі зразків вздовж осі у. (тобто де фактично знаходяться ваші дані).
Якщо значення даних йдуть по приблизно прямій лінії, що утворює кут 45 градусів, то дані вважаються нормально розподіленими.

Ви також можете виконати формальний статистичний тест, щоб визначити, чи є змінна нормально розподіленою.
Якщо p-значення тесту нижче певного рівня значущості (наприклад, α = 0,05), то у вас є достатньо доказів того, що дані не розподілені нормально.
Існує три статистичні тести, які зазвичай використовуються для перевірки нормальності:
1. Тест Жарке-Бера
- Як виконати тест Жарке-Бера в Excel
- Як виконати тест Жарке-Бера в R
- Як виконати тест Jarque-Bera в Python
2. Тест Шапіро-Вілка
3. Тест Колмогорова-Смирнова
Гіпотеза 4: Споріднені пари
Коефіцієнт кореляції Пірсона також передбачає, що кожне спостереження в наборі даних має мати пару значень.
Цю гіпотезу легко перевірити. Наприклад, якщо ви обчислюєте кореляцію між вагою та зростом, просто переконайтеся, що кожне спостереження в наборі даних має міру ваги та міру зростання.
Гіпотеза 5: відсутність викидів
Коефіцієнт кореляції Пірсона також припускає, що в наборі даних немає екстремальних викидів, оскільки викиди сильно впливають на обчислення коефіцієнта кореляції.
Щоб проілюструвати це, розглянемо наступний набір даних:
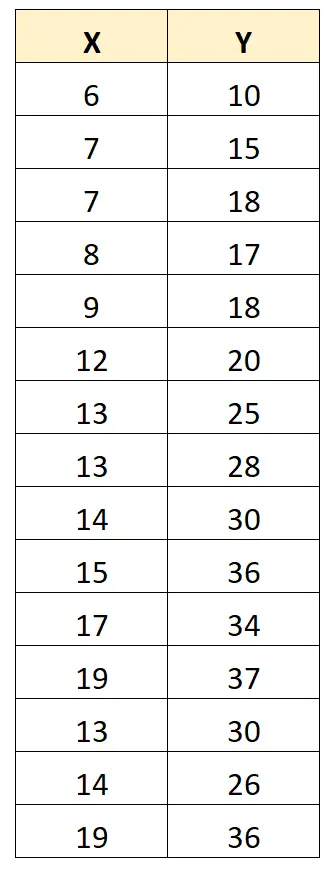
Коефіцієнт кореляції Пірсона між X і Y становить 0,949 .
Однак припустімо, що в наборі даних є викид:
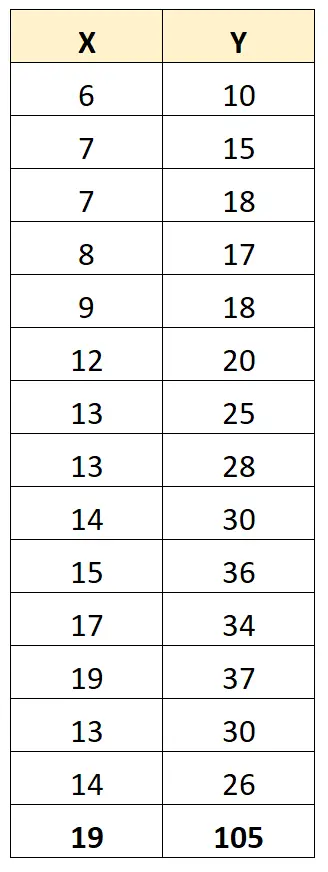
Коефіцієнт кореляції Пірсона між X і Y тепер становить 0,711 .
Викид суттєво змінює коефіцієнт кореляції Пірсона між двома змінними. У цьому випадку може мати сенс видалити викид із набору даних.
Пов’язане: Повний посібник: коли потрібно видаляти викиди в даних
Додаткові ресурси
Наступні посібники надають додаткову інформацію про кореляцію Пірсона:
Введення в коефіцієнт кореляції Пірсона
Як повідомити про кореляцію Пірсона у форматі APA
Як вручну обчислити коефіцієнт кореляції Пірсона