П'ять припущень множинної лінійної регресії

Множинна лінійна регресія – це статистичний метод, який ми можемо використовувати для розуміння зв’язку між декількома змінними предикторів і змінною відповіді .

Однак перед виконанням множинної лінійної регресії ми повинні спочатку переконатися, що виконуються п’ять припущень:

1. Лінійний зв’язок: існує лінійний зв’язок між кожною змінною предиктора та змінною відповіді.

2. Відсутність мультиколінеарності: жодна з прогностичних змінних не сильно корельована одна з одною.

3. Незалежність: спостереження є незалежними.

4. Гомоскедастичність: залишки мають постійну дисперсію в кожній точці лінійної моделі.

5. Багатовимірна нормальність: модельні залишки розподілені нормально.

Якщо одне або декілька з цих припущень не виконуються, то результати множинної лінійної регресії можуть бути ненадійними.

У цій статті ми надаємо пояснення для кожного припущення, як визначити, чи виконується припущення, і що робити, якщо припущення не виконується.

Гіпотеза 1: Лінійний зв’язок

Множинна лінійна регресія припускає, що існує лінійна залежність між кожною змінною предиктора та змінною відповіді.

Як визначити, чи виконується це припущення

Найпростіший спосіб визначити, чи виконується це припущення, — створити діаграму розсіювання кожної змінної предиктора та змінної відповіді.

Це дозволяє візуально побачити, чи існує лінійна залежність між двома змінними.

Якщо точки на діаграмі розсіювання лежать приблизно вздовж прямої діагональної лінії, ймовірно, існує лінійна залежність між змінними.

Наприклад, точки на графіку нижче, здається, падають на пряму лінію, що вказує на наявність лінійного зв’язку між цією конкретною змінною предиктором (x) і змінною відповіді (y):

Що робити, якщо це припущення не виконується

Якщо між однією або декількома змінними предиктора та змінною відповіді немає лінійного зв’язку, у нас є кілька варіантів:

1. Застосуйте нелінійне перетворення до змінної предиктора, наприклад, взявши логарифм або квадратний корінь. Це часто може перетворити відносини на більш лінійні.

2. Додайте іншу змінну предиктора до моделі. Наприклад, якщо графік залежності x від y має параболічну форму, може мати сенс додати X ² як додаткову змінну предиктора в моделі.

3. Видаліть змінну предиктора з моделі. У крайньому випадку, якщо немає лінійного зв’язку між певною змінною предиктора та змінною відповіді, тоді може бути некорисним включати змінну предиктора в модель.

Гіпотеза 2: відсутність мультиколінеарності

Множинна лінійна регресія припускає, що жодна з прогностичних змінних не сильно корелює одна з одною.

Коли одна або більше змінних предиктора сильно корельовані, регресійна модель страждає від мультиколінеарності , що робить оцінки коефіцієнтів моделі ненадійними.

Як визначити, чи виконується це припущення

Найпростіший спосіб визначити, чи виконується це припущення, — обчислити значення VIF для кожної змінної предиктора.

Значення VIF починаються з 1 і не мають верхньої межі. Як правило, значення VIF вище 5* вказують на потенційну мультиколінеарність.

У наступних посібниках показано, як розрахувати VIF у різних статистичних програмах:

• Як розрахувати VIF в R
• Як розрахувати VIF у Python
• Як розрахувати VIF в Excel

*Іноді дослідники замість цього використовують значення VIF 10, залежно від галузі дослідження.

Що робити, якщо це припущення не виконується

Якщо одна або кілька змінних предиктора мають значення VIF більше 5, найпростіший спосіб вирішити цю проблему — просто видалити змінну(і) предиктора з високими значеннями VIF.

Крім того, якщо ви хочете зберегти кожну змінну предиктора в моделі, ви можете використати інший статистичний метод, наприклад регресію хребта , ласо регресію або часткову регресію найменших квадратів , розроблену для обробки сильно корельованих змінних предиктора.

Гіпотеза 3: Незалежність

Множинна лінійна регресія передбачає, що кожне спостереження в наборі даних є незалежним.

Як визначити, чи виконується це припущення

Найпростіший спосіб визначити, чи виконується це припущення, — виконати тест Дарбіна-Ватсона , який є формальним статистичним тестом, який повідомляє нам, чи мають залишки (а отже, і спостереження) автокореляцію.

Що робити, якщо це припущення не виконується

Залежно від того, як це припущення порушено, у вас є кілька варіантів:

• Для позитивної послідовної кореляції розгляньте можливість додавання лагів залежної та/або незалежної змінної до моделі.
• Для негативної послідовної кореляції переконайтеся, що жодна з ваших змінних не має надмірної затримки .
• Для сезонної кореляції розгляньте можливість додавання сезонних фіктивних елементів до моделі.

Гіпотеза 4: гомоскедастичність

Множинна лінійна регресія передбачає, що залишки мають постійну дисперсію в кожній точці лінійної моделі. Коли це не так, залишки страждають від гетероскедастичності .

Коли гетероскедастичність присутня в регресійному аналізі, результати регресійної моделі стають ненадійними.

Зокрема, гетероскедастичність збільшує дисперсію оцінок коефіцієнта регресії, але регресійна модель не враховує це. Це значно підвищує ймовірність того, що регресійна модель стверджуватиме, що термін у моделі є статистично значущим, хоча насправді це не так.

Як визначити, чи виконується це припущення

Найпростіший спосіб визначити, чи виконується це припущення, — створити графік стандартизованих залишків проти прогнозованих значень.

Після підгонки регресійної моделі до набору даних можна створити діаграму розсіювання, яка відображає прогнозовані значення змінної відповіді на осі х і стандартизовані залишки моделі на осі х. р.

Якщо точки на діаграмі розсіювання демонструють тенденцію, то наявна гетероскедастичність.

На наступній діаграмі показано приклад регресійної моделі, у якій гетероскедастичність не є проблемою:

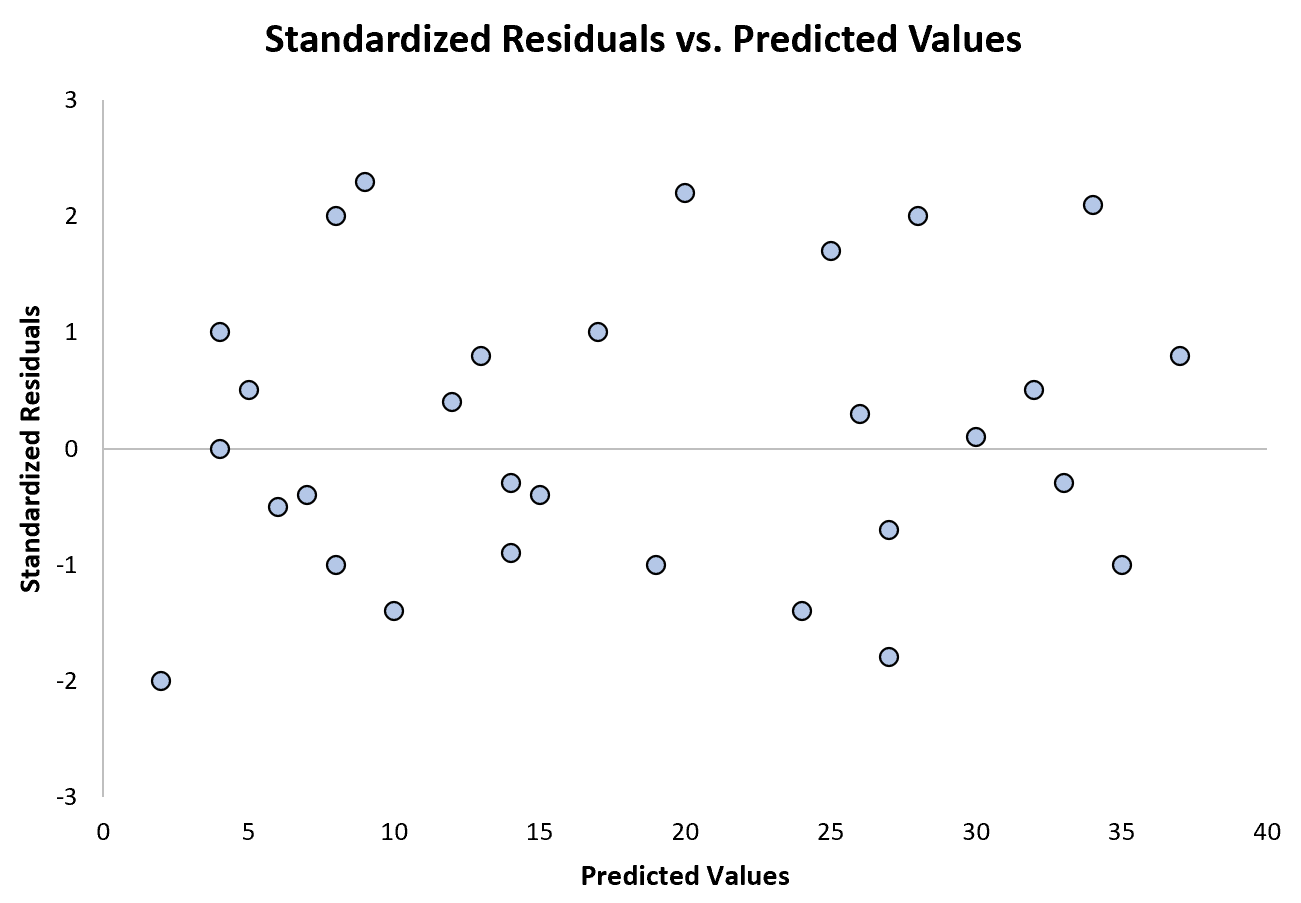
Зверніть увагу, що стандартизовані залишки розкидані навколо нуля без чіткої моделі.

На наступній діаграмі показано приклад регресійної моделі, де гетероскедастичність є проблемою:

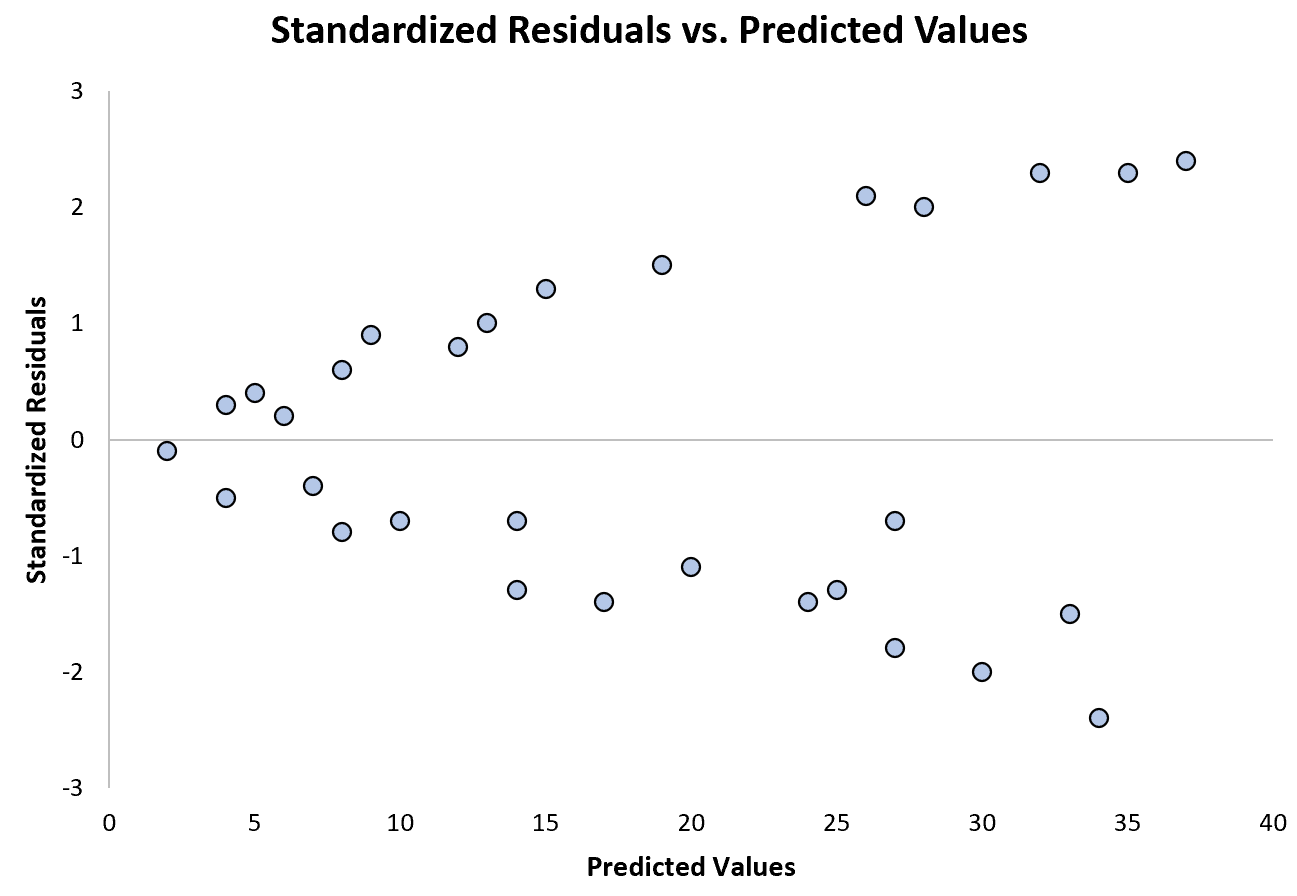
Зверніть увагу, як стандартизовані залишки розповсюджуються все більше і більше в міру зростання прогнозованих значень. Ця форма «конуса» є класичною ознакою гетероскедастичності:

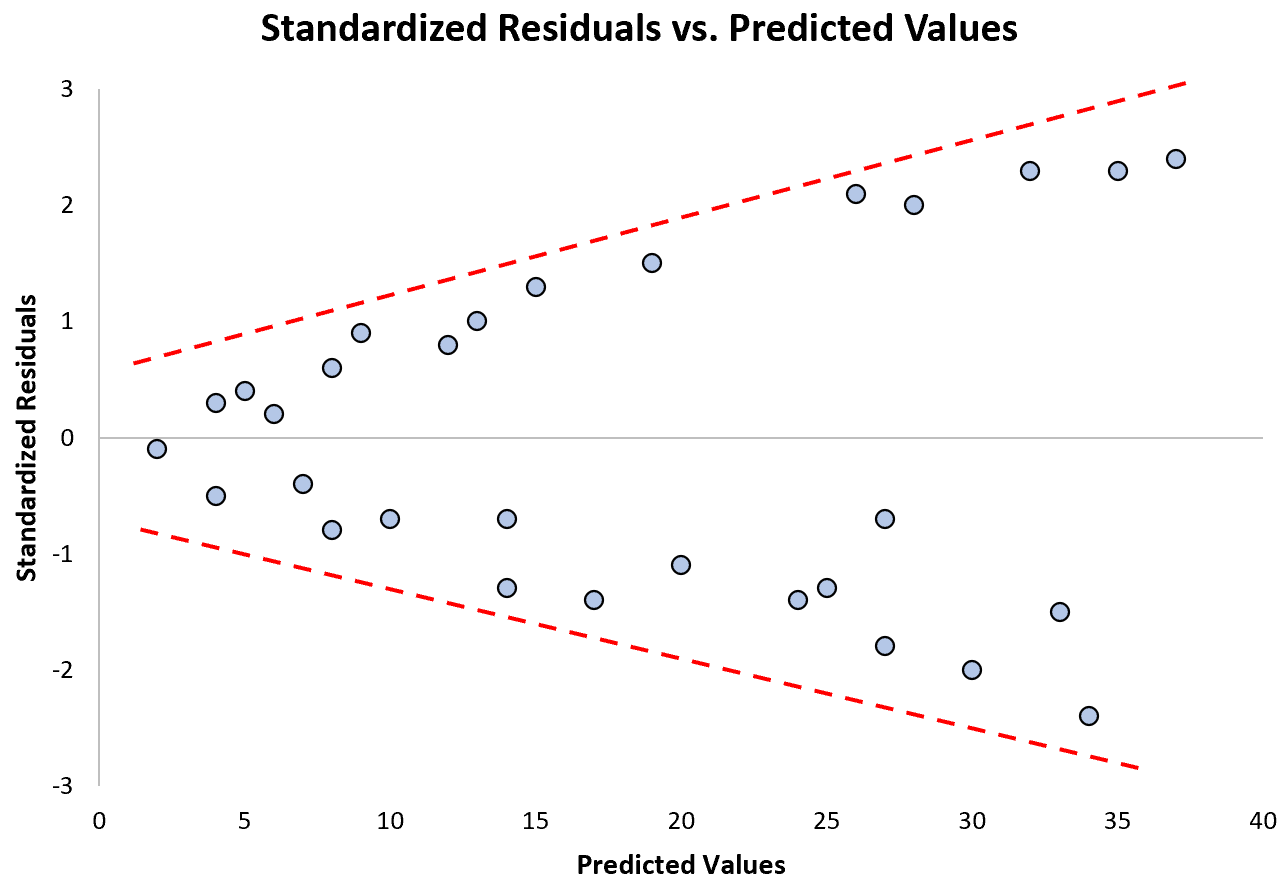
Що робити, якщо це припущення не виконується

Існує три поширених способи корекції гетероскедастичності:

1. Перетворення змінної відповіді. Найбільш поширеним способом боротьби з гетероскедастичністю є перетворення змінної відповіді шляхом отримання логарифму, квадратного або кубічного кореня з усіх значень змінної відповіді. Це часто призводить до зникнення гетероскедастичності.

2. Перевизначте змінну відповіді. Один із способів перевизначити змінну відповіді — використовувати швидкість , а не вихідне значення. Наприклад, замість того, щоб використовувати чисельність населення для прогнозування кількості флористів у місті, ми можемо використовувати чисельність населення для прогнозування кількості флористів на душу населення.

У більшості випадків це зменшує мінливість, яка природно виникає у великих популяціях, оскільки ми вимірюємо кількість флористів на людину, а не саму кількість флористів.

3. Використовуйте зважену регресію. Інший спосіб виправлення гетероскедастичності — це використання зваженої регресії, яка призначає вагу кожній точці даних на основі дисперсії її підігнаного значення.

По суті, це дає низькі ваги точкам даних, які мають більшу дисперсію, зменшуючи їхні залишкові квадрати. Якщо використовуються відповідні ваги, це може усунути проблему гетероскедастичності.

Пов’язане : Як виконати зважену регресію в R

Припущення 4: Багатовимірна нормальність

Множинна лінійна регресія передбачає, що модельні залишки розподілені нормально.

Як визначити, чи виконується це припущення

Існує два поширених способи перевірити, чи виконується це припущення:

1. Візуально перевірте гіпотезу за допомогою графіків QQ .

Діаграма QQ, скорочення від quantile-quantile plot, — це тип графіка, який ми можемо використовувати, щоб визначити, чи відповідають залишки моделі нормальному розподілу. Якщо точки на графіку приблизно утворюють пряму діагональну лінію, тоді виконується припущення про нормальність.

Наступний графік QQ показує приклад залишків, які приблизно відповідають нормальному розподілу:

Однак наведений нижче графік QQ показує приклад випадку, коли залишки чітко відхиляються від прямої діагональної лінії, що вказує на те, що вони не відповідають нормальному розподілу:

2. Перевірте гіпотезу за допомогою формального статистичного тесту, такого як Шапіро-Вілка, Колмогорова-Смиронова, Жарка-Барре або Д’Агостіно-Пірсона.

Майте на увазі, що ці тести чутливі до великих розмірів вибірки, тобто вони часто роблять висновок, що залишки не є нормальними, коли розмір вашої вибірки надзвичайно великий. Ось чому для перевірки цієї гіпотези часто простіше використовувати графічні методи, такі як графік QQ.

Що робити, якщо це припущення не виконується

Якщо припущення про нормальність не виконується, у вас є кілька варіантів:

1. По-перше, перевірте, чи немає в даних екстремальних викидів, які призводять до порушення припущення про нормальність.

2. Потім ви можете застосувати нелінійне перетворення до змінної відповіді, наприклад, взявши квадратний корінь, логарифм або кубічний корінь усіх значень змінної відповіді. Це часто призводить до більш нормального розподілу модельних залишків.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про множинну лінійну регресію та її припущення.

Вступ до множинної лінійної регресії
Керівництво з гетероскедастичності в регресійному аналізі
Посібник із мультиколінеарності та VIF у регресії

У наступних посібниках наведено покрокові приклади виконання множинної лінійної регресії за допомогою різного статистичного програмного забезпечення:

Як виконати множинну лінійну регресію в Excel
Як виконати множинну лінійну регресію в R
Як виконати множинну лінійну регресію в SPSS
Як виконати множинну лінійну регресію в Stata