Як виконати двовимірний аналіз у python: із прикладами

Термін двовимірний аналіз стосується аналізу двох змінних. Ви можете запам’ятати це, тому що префікс “бі” означає “два”.

Метою двофакторного аналізу є розуміння зв’язку між двома змінними

Існує три поширених способи виконання двовимірного аналізу:

1. Хмари точок

2. Коефіцієнти кореляції

3. Проста лінійна регресія

У наведеному нижче прикладі показано, як виконати кожен із цих типів двовимірного аналізу в Python, використовуючи такий pandas DataFrame, який містить інформацію про дві змінні: (1) години, витрачені на навчання, і (2) іспитовий бал, отриманий 20 різними студентами:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. Хмари точок

Ми можемо використати такий синтаксис, щоб створити діаграму розсіювання вивчених годин і результатів іспитів:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

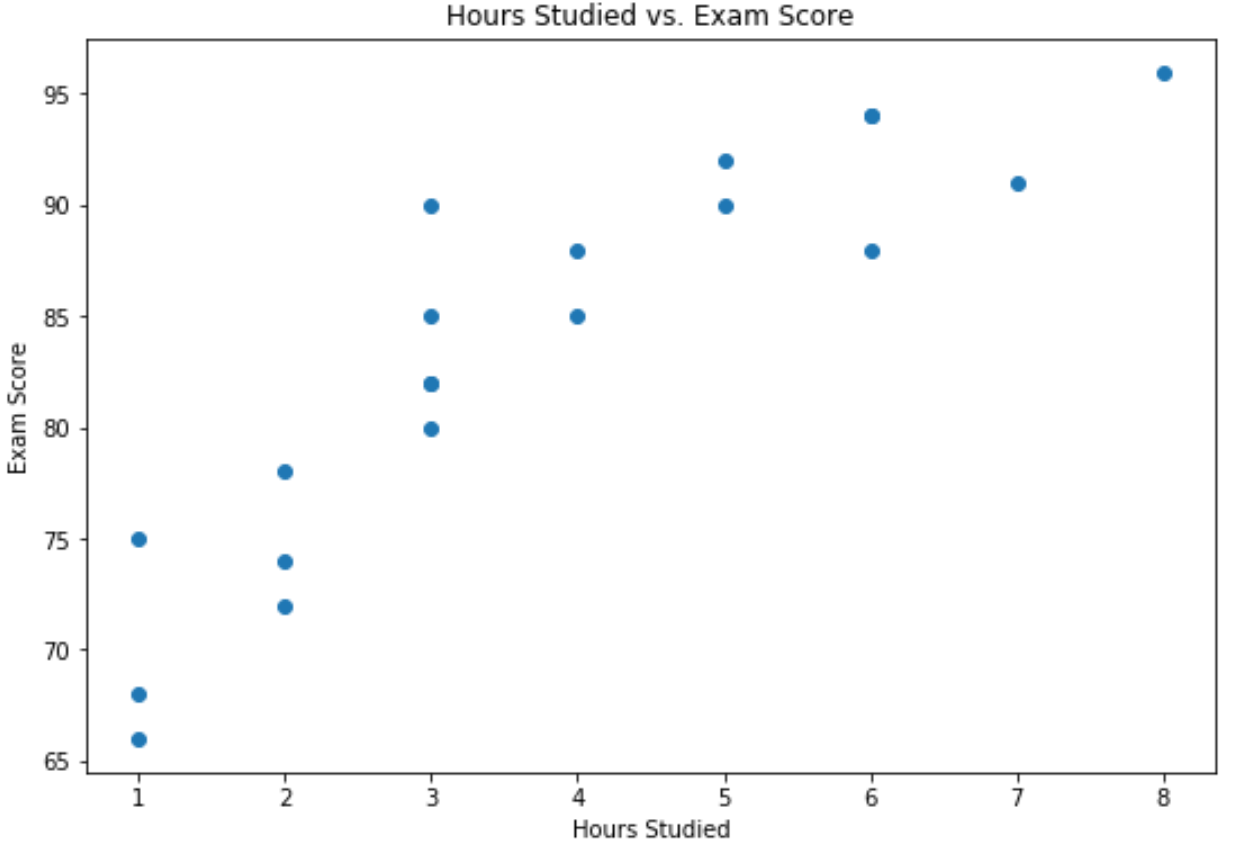
На осі абсцис відкладено кількість годин, а на осі у – оцінка, отримана на іспиті.

На графіку видно, що існує позитивний зв’язок між двома змінними: зі збільшенням кількості годин навчання результати іспитів також мають тенденцію до зростання.

2. Коефіцієнти кореляції

Коефіцієнт кореляції Пірсона — це спосіб кількісного визначення лінійного зв’язку між двома змінними.

Ми можемо використовувати функцію corr() у pandas для створення кореляційної матриці:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

Коефіцієнт кореляції виявляється рівним 0,891 . Це вказує на сильну позитивну кореляцію між вивченими годинами та оцінкою іспиту.

3. Проста лінійна регресія

Проста лінійна регресія — це статистичний метод, який ми можемо використовувати для кількісного визначення зв’язку між двома змінними.

Ми можемо використати функцію OLS() із пакету statsmodels, щоб швидко підібрати просту лінійну регресійну модель для годин, які вивчалися, і отриманих результатів іспитів:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

Підігнане рівняння регресії виявляється таким:

Оцінка за іспит = 69,0734 + 3,8471*(вивчені години)

Це говорить нам про те, що кожна додаткова вивчена година пов’язана із середнім збільшенням оцінки за іспит на 3,8471 .

Ми також можемо використати підігнане рівняння регресії, щоб передбачити бал, який отримає студент на основі загальної кількості вивчених годин.

Наприклад, студент, який навчається 3 години, повинен отримати 81,6147 :

• Оцінка за іспит = 69,0734 + 3,8471*(вивчені години)
• Оцінка за іспит = 69,0734 + 3,8471*(3)
• Результат іспиту = 81,6147

Додаткові ресурси

У наступних посібниках надається додаткова інформація про двовимірний аналіз:

Вступ до двовимірного аналізу
5 прикладів двовимірних даних у реальному житті
Вступ до простої лінійної регресії
Вступ до коефіцієнта кореляції Пірсона