Як вручну виконати двосторонній дисперсійний аналіз
Двосторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп, які були розділені за двома факторами.
У цьому посібнику пояснюється, як вручну виконати двосторонній дисперсійний аналіз.
Приклад: ручний двосторонній дисперсійний аналіз
Припустімо, ботанік хоче знати, чи впливає на ріст рослин сонячне світло та частота поливу. Вона висаджує 40 насінин і дає їм рости протягом місяця в різних умовах сонячного освітлення та частоти поливу.
Через місяць вона записує висоту кожної рослини. Результати наведені нижче:

У таблиці вище ми бачимо, що в кожній комбінації умов було вирощено п’ять рослин.
Наприклад, п’ять рослин вирощували з щоденним поливом і без сонячного світла, і їхня висота через два місяці становила 4,8 дюйма, 4,4 дюйма, 3,2 дюйма, 3,9 дюйма та 4,4 дюйма:

Ми можемо використати такі кроки, щоб виконати двосторонній дисперсійний аналіз:
Крок 1: Обчисліть суму квадратів для першого фактора (частота поливу)
Спочатку ми обчислимо загальну середню висоту 40 рослин:
Загальний середній = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525
Далі розрахуємо середню висоту всіх рослин, які поливають щодня:
Середньоденний = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155
Далі ми обчислимо середню висоту всіх рослин, які поливали щотижня:
Середнє за тиждень = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15
Далі розрахуємо суму квадратів коефіцієнта «частота поливу» за такою формулою:
Σn(X j – X ..) 2
золото:
- n : розмір вибірки групи j
- Σ : грецький символ, що означає «сума»
- X j : середнє значення групи j
- X .. : великий середній
У нашому прикладі ми обчислюємо суму квадратів коефіцієнта «частота поливу» таким чином: 20(5,155-5,1525) 2 + 20(5,15-5,1525) 2 = 0,00025
Крок 2: обчисліть суму квадратів для другого фактора (вплив сонця)
Спочатку ми обчислимо загальну середню висоту 40 рослин:
Загальний середній = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525
Далі розрахуємо середню висоту всіх рослин, які не піддаються впливу сонця:
Середнє без сонця = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07
Ми повторимо цей розрахунок, щоб знайти середню висоту рослин, які зазнали різного сонячного впливу:
- Середній рівень сонячного світла = 5,1
- Середнє середнє сонячне світло = 5,89
- Середня висока сонячність = 5,55
Далі ми обчислимо суму квадратів для коефіцієнта «освіти сонця» за такою формулою:
Σn(X j – X ..) 2
золото:
- n : розмір вибірки групи j
- Σ : грецький символ, що означає «сума»
- X j : середнє значення групи j
- X .. : великий середній
У нашому прикладі ми обчислюємо суму квадратів фактора «освітлення сонцем» таким чином: 10(4,07-5,1525) 2 + 10(5,1-5,1525) 2 + 10(5,89 -5,1525) 2 + 10(5,55-5,1525) 2 = 18,76475
Крок 3: обчисліть суму квадратів усередині (помилка)
Далі ми розрахуємо суму квадратів, взявши суму квадратів різниць між кожною комбінацією факторів і висотою окремих рослин.
Наприклад, середня висота всіх рослин, які поливають щодня без сонячного світла, становить 4,14. Потім ми можемо обчислити суму квадратів різниць для кожної з цих окремих рослин наступним чином:
- СС для щоденного поливу і без сонця: (4,8-4,14) 2 + (4,4-4,14) 2 + (3,2-4,14) 2 + (3,9-4,14) 2 + (4,4-4,14) 2 = 1,512
Ми можемо повторити цей процес для кожної комбінації факторів:
- SS для щоденного поливу і слабкого сонячного освітлення: 0,928
- SS для щоденного поливу та середньої сонячності: 1,788
- SS для щоденного поливу і сильного сонячного світла: 1,648
- СС при тижневому поливі без сонця: 0,34
- SS для щотижневого поливу і слабкого сонячного світла: 0,548
- SS для тижневого поливу і середньої сонячності: 0,652
- SS для щотижневого поливу і сильного сонячного світла: 1,268
Потім ми можемо взяти суму всіх цих значень, щоб знайти суму квадратів усередині (помилка):
Суми квадратів у межах = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684
Крок 4: обчисліть загальну суму квадратів
Тоді ми можемо обчислити загальну суму квадратів, взявши суму різниць між висотою кожної рослини та великим середнім:
Загальна сума квадратів = (4,8 – 5,1525) 2 + (5 – 5,1525) 2 + … + (5,5 – 5,1525) 2 = 28,45975
Крок 5: обчисліть суму квадратів взаємодії
Далі ми обчислимо суму квадратів взаємодії за такою формулою:
- Взаємодія SS = SS Total – SS Фактор 1 – SS Фактор 2 – SS Interior
- Взаємодія SS = 28,45975 – 0,00025 – 18,76475 – 8,684
- SS взаємодія = 1,01075
Крок 6: Заповніть таблицю ANOVA
Нарешті, ми заповнимо значення з двосторонньої таблиці ANOVA:
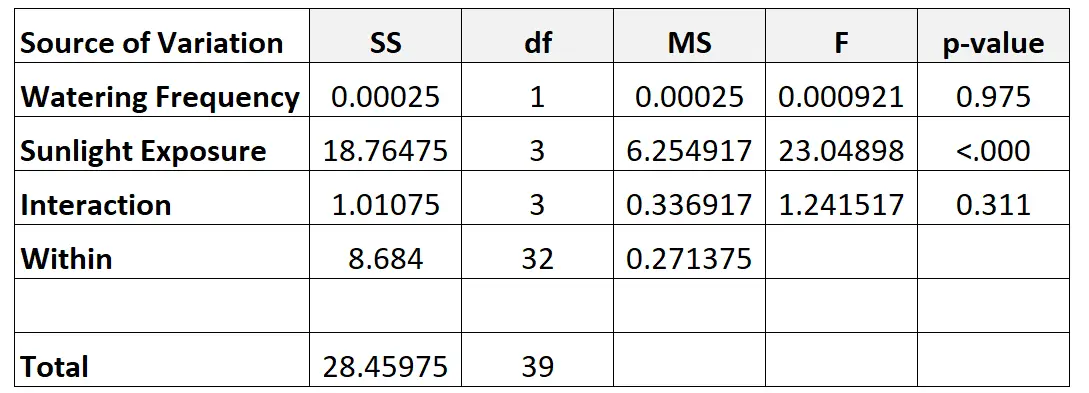
Ось як ми розрахували різні числа в таблиці:
- df Частота поливу: d-1 = 2-1 = 1
- df Вплив сонця: k-1 = 4-1 = 3
- dfВзаємодія : (j-1)*(k-1) = 1*3 = 3
- df In : n – (j*k) = 40 – (2*4) = 32
- загальний df: n-1 = 40-1 = 39
- MS: SS/DF
- Частота поливу F : частота поливу MS/MS у приміщенні
- F Вплив сонячного світла : MS / MS вплив сонячного світла в приміщенні
- Взаємодія F : Взаємодія MS / MS Within
- p-значення частоти поливу : p-значення, яке відповідає F-значенню 0,000921 з чисельником df = 1 і знаменником df = 32
- P-value впливу сонця : p-value, яке відповідає F-значенню 23,04898 з чисельником df = 3 і знаменником df = 32
- Взаємодія p-value : P-значення, яке відповідає F-значенню 1,241517 з чисельником df = 3 і знаменником df = 32
Примітка №1: n = загальна кількість спостережень, j = кількість рівнів для частоти поливу, k = кількість рівнів для впливу сонця.
Примітка №2 : P-значення, які відповідають F-значенню, були розраховані за допомогою калькулятора F-розподілу.
Крок 7: Інтерпретація результатів
З таблиці ANOVA ми можемо спостерігати наступне:
- P-значення для взаємодії між частотою поливу та сонячним промінням становило 0,311 . Це не є статистично значущим при α = 0,05.
- P-значення частоти поливу становило 0,975 . Це не є статистично значущим при α = 0,05.
- P-значення для перебування на сонці становило <0,000 . Це статистично значуще при α = 0,05.
Ці результати показують, що сонячне опромінення є єдиним фактором зі статистично значущим впливом на висоту рослин.
А оскільки немає ефекту взаємодії, вплив сонячного випромінювання є постійним на кожному рівні частоти поливу.
Простіше кажучи, те, щодня чи щотижня поливають рослину, не впливає на вплив сонця на рослину.
Додаткові ресурси
У наступних посібниках надається додаткова інформація про ANOVA:
Як вручну виконати односторонній дисперсійний аналіз
Як вручну виконати повторний аналіз ANOVA
Повний посібник: як звітувати про результати двостороннього дисперсійного аналізу