Як виконати двосторонній дисперсійний аналіз у sas

Двосторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп, які були віднесені до двох змінних (іноді їх називають «факторами»).

Цей підручник надає покроковий приклад того, як виконати двосторонній дисперсійний аналіз у SAS.

Крок 1: Створіть дані

Припустімо, ботанік хоче знати, чи впливає на ріст рослин сонячне світло та частота поливу.

Вона висаджує 30 насінин і дає їм рости протягом місяця в різних умовах сонячного освітлення та частоти поливу. Через місяць вона записує висоту кожної рослини. Результати наведені нижче:

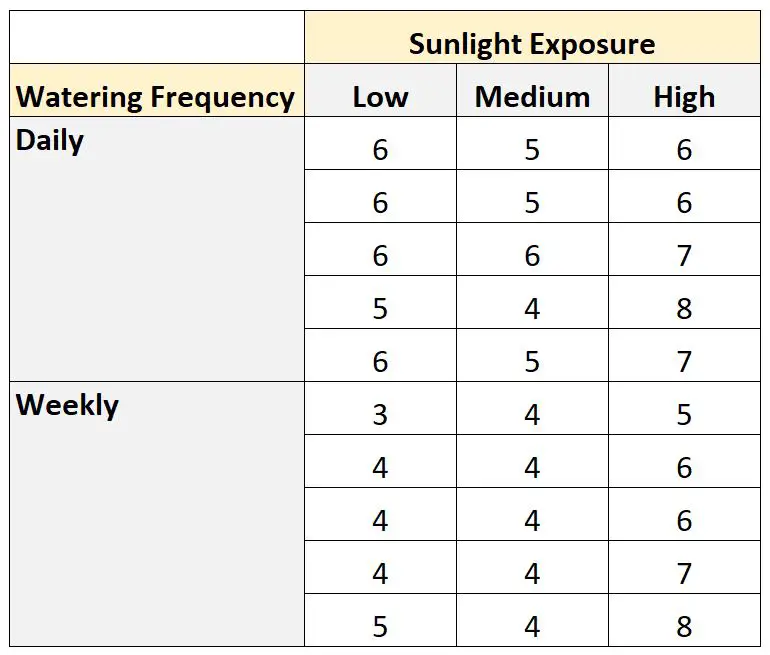
Ми можемо використати такий код, щоб створити цей набір даних у SAS:

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

Крок 2: Виконайте двосторонній дисперсійний аналіз

Далі ми використаємо proc ANOVA для виконання двостороннього дисперсійного аналізу:

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

Крок 3: Інтерпретація результатів

Перша таблиця, яку ми хочемо проаналізувати в результатах, це таблиця ANOVA:

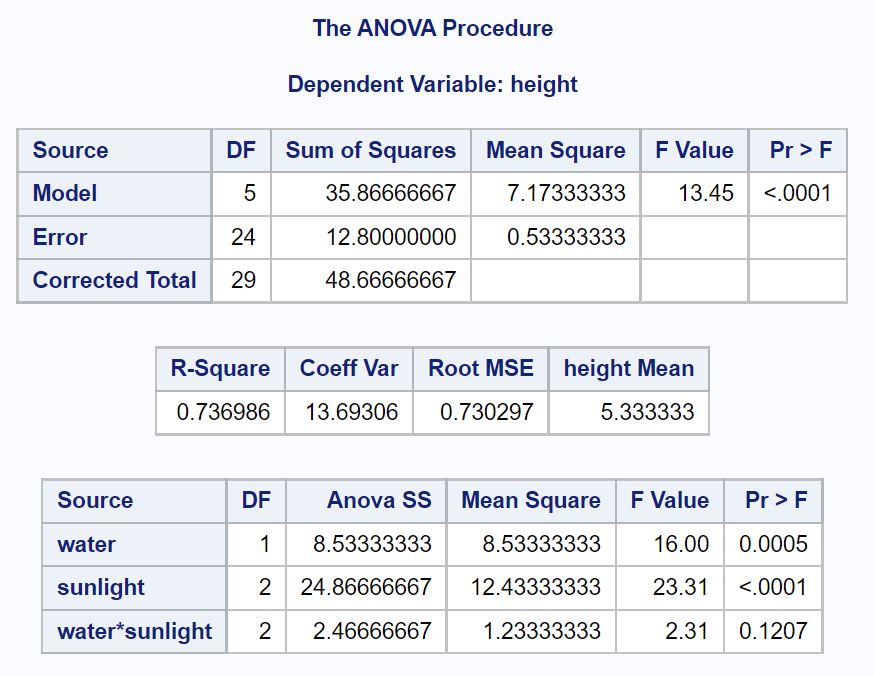
З цієї таблиці ми бачимо:

• P-значення для води: 0,0005
• P-значення для сонячного світла: <.0001
• P-значення для взаємодії між водою та сонячним світлом: . 1207

Це говорить нам про те, що вода та сонячне світло є статистично значущими прогностичними факторами висоти рослин і що немає статистично значущого ефекту взаємодії між водою та сонячним світлом.

Далі ми можемо вивчити результати пост-тестів Тьюкі, щоб визначити, які рівні води та сонячного світла статистично суттєво відрізняються.

По-перше, ми розглянемо аналітичні порівняння Тьюкі щодо води:

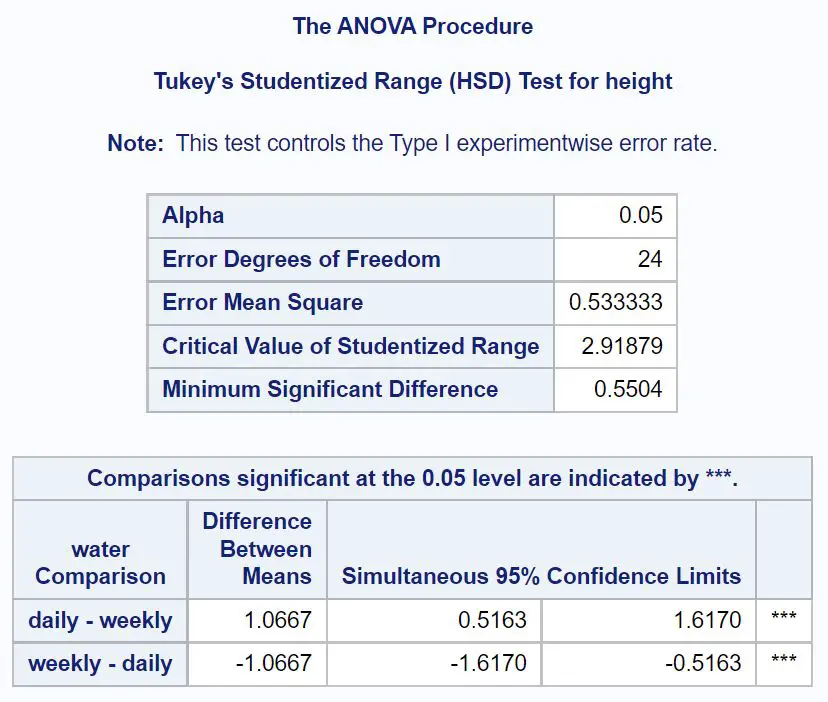
З результатів ми бачимо, що середня різниця у висоті рослин, які поливали щодня та щотижня, становила 1,0667 дюйма.

95% довірчий інтервал для різниці в середньому розмірі становить [0,5163, 1,6170] . Це означає, що ми на 95% впевнені, що справжня різниця в середній висоті між рослинами, які поливають щодня, і рослинами, які поливають щотижня, становить від 0,5163 дюйма до 1,6170 дюйма.

По-перше, ми розглянемо аналітичні порівняння Тьюкі щодо сонячного світла:

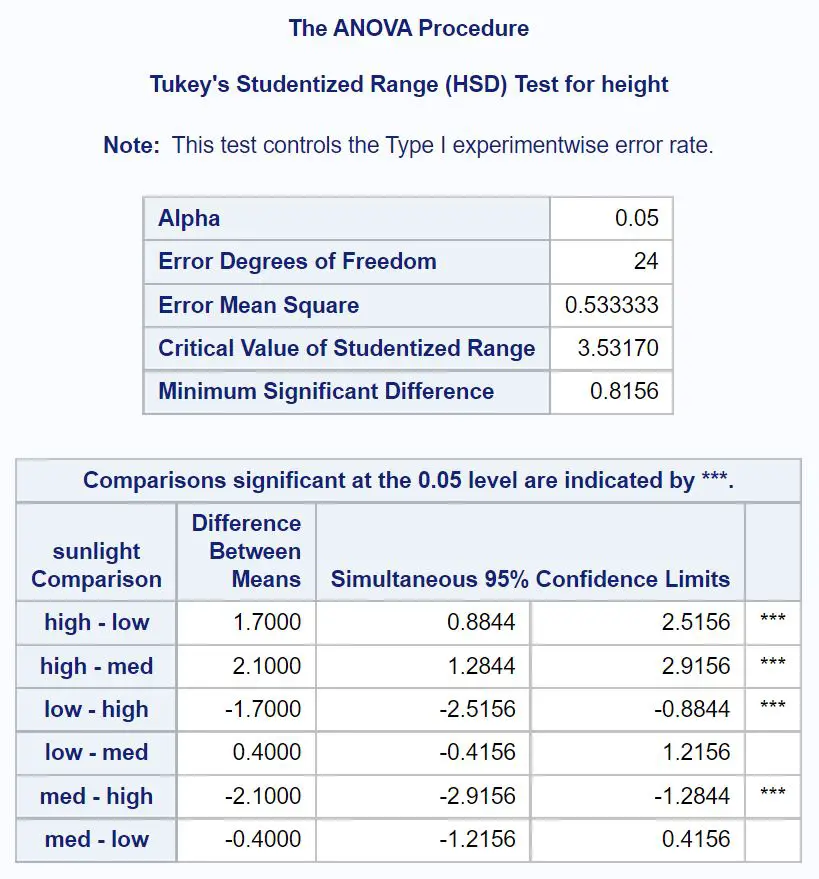
Щоб з’ясувати, які середні групи відрізняються, нам потрібно подивитися, які парні порівняння мають зірочки ( *** ).

З таблиці ми бачимо, що середні значення наступних груп статистично значимо відрізняються:

• Високе або слабке сонячне світло (95% ДІ = [0,8844, 2,5156])
• Сильне або середнє сонячне світло (95% ДІ = [1,2844, 2,9156])

Крок 4: звіт про результати

Нарешті, ми можемо повідомити про результати двостороннього дисперсійного аналізу:

Двосторонній дисперсійний аналіз був проведений для аналізу впливу частоти поливу та впливу сонця на ріст рослин.

Двосторонній дисперсійний аналіз виявив, що не було статистично значущої взаємодії між ефектами частоти поливу та впливу сонця (p = 0,1207).

Простий аналіз впливу рук показав, що частота поливу мала статистично значущий вплив на ріст рослин (p = 0,0005).

Простий аналіз впливу рук показав, що вплив сонця також мав статистично значущий вплив на ріст рослин (p < 0,0001).

Додаткові ресурси

У наступних посібниках надається додаткова інформація про двосторонній дисперсійний аналіз:

Вступ до двостороннього дисперсійного аналізу
Односторонній або двосторонній ANOVA: коли їх використовувати?
Як вручну виконати двосторонній дисперсійний аналіз