Коваріаційна матриця

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке коваріаційна матриця та яка її формула. Ви дізнаєтесь, як створити коваріаційну матрицю на конкретному прикладі та про властивості коваріаційних матриць.

Що таке коваріаційна матриця?

Коваріаційна матриця – це квадратна матриця, елементами якої є дисперсії та коваріації досліджуваних змінних. Таким чином, елементи головної діагоналі коваріаційної матриці є дисперсією кожної змінної, а решта елементів є коваріаціями між змінними.

У статистиці коваріаційна матриця використовується для аналізу зв’язку між двома або більше випадковими величинами. Коваріаційна матриця дуже корисна, оскільки дозволяє швидко інтерпретувати кореляцію між багатьма змінними, оскільки ви можете бачити значення всіх коваріацій змінних одночасно.

Символом коваріаційної матриці є велика грецька літера сигма (Σ).

Як розрахувати коваріаційну матрицю

Для розрахунку коваріаційної матриці кількох статистичних змінних необхідно виконати наступні кроки:

Обчисліть дисперсії всіх змінних.
Обчисліть коваріацію кожної пари змінних.
Сформуйте коваріаційну матрицю:

Дисперсія змінної i повинна бути розміщена на головній діагоналі матриці, точніше в позиції i,i .
Коваріація між змінними i та j має бути розміщена в позиції i,j матриці.

Таким чином , формула для коваріаційної матриці виглядає наступним чином:

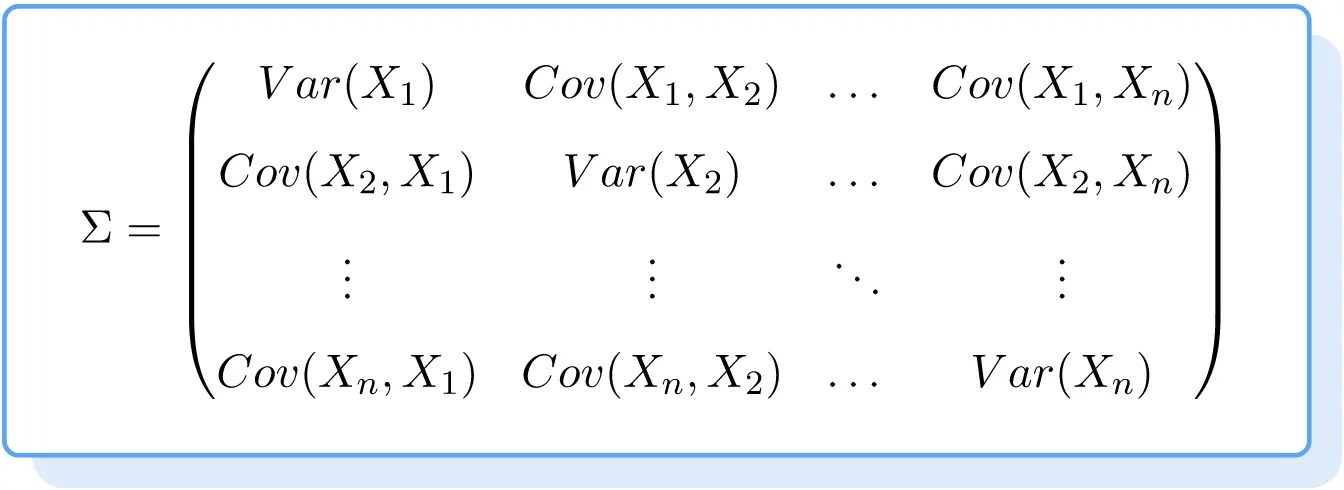
Приклад коваріаційної матриці

Ознайомившись із визначенням коваріаційної матриці, нижче наведено покрокову вправу, щоб ви могли побачити, як створюється цей тип матриці.

Обчислює коваріаційну матрицю змінних X, Y і Z, значення яких:

X: 4, 7, 12, 5, 7
І: 9, 15, 19, 6, 8
Я: 7, 2, 4, 6, 3

Перше, що нам потрібно зробити, це визначити дисперсії всіх змінних:

$Var(X)=7,6$

$Var(Y)=23,44$

$Var(Z)=3,44$

➤ Дивіться: калькулятор розриву

По-друге, ми знаходимо коваріацію між кожною парою змінних:

$Cov(X,Y)=11,2$

$Cov(X,Z)=-2,6$

$Cov(Y,Z)=-4,36$

➤ Дивіться: калькулятор коваріації

І коли ми обчислили всі дисперсії та коваріації, все, що залишилося, це скласти коваріаційну матрицю. Для цього розміщуємо значення дисперсії на головній діагоналі матриці, а значення коваріації у відповідну їм позицію:

$\Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}$

$\Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}$

Як бачите, представляючи дисперсії та коваріації в матриці, дуже легко інтерпретувати змінні. Змінною з найбільшою дисперсією є Y (23.44), з іншого боку, змінні X і Y мають прямий зв’язок, тоді як змінні X і Z (а отже, Y і Z) мають обернений зв’язок.

Зверніть увагу, що коваріаційна матриця завжди симетрична, оскільки коваріація між двома змінними не залежить від порядку змінних. Наприклад,

$Cov(X,Y)$

дорівнює

$Cov(Y,X).$

Крім того, коваріаційна матриця завжди буде квадратною матрицею, а її розмір дорівнюватиме кількості змінних. У цьому випадку ми мали три змінні, і тому це матриця 3×3, але якби у нас було лише дві змінні, коваріаційна матриця була б 2×2.

Властивості коваріаційної матриці

Коваріаційна матриця має такі характеристики:

Коваріаційна матриця – це квадратна матриця порядку числа змінних.
Коваріаційна матриця є симетричною, це означає, що головна діагональ матриці є віссю симетрії.
Коваріаційна матриця завжди додатна напіввизначена.
Визначник коваріаційної матриці дорівнює або більше нуля.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше