Введення в дерева класифікації та регресії

Коли зв’язок між набором змінних предикторів і змінною відповіді є лінійним, такі методи, як множинна лінійна регресія, можуть створити точні прогнозні моделі.

Однак, коли зв’язок між набором предикторів і відповіддю дуже нелінійний і складний, нелінійні методи можуть працювати краще.

Прикладом нелінійного методу є дерева класифікації та регресії , які часто називають абревіатурою CART .

Як випливає з назви, моделі CART використовують набір змінних прогнозів для створення дерев рішень , які передбачають значення змінної відповіді.

Наприклад, припустімо, що ми маємо набір даних, що містить змінні прогнозу « Зіграні роки » та «Середня кількість хоум-ранів» , а також змінну відповіді « Річна зарплата» для сотень професійних гравців у бейсбол.

Ось як може виглядати дерево регресії для цього набору даних:

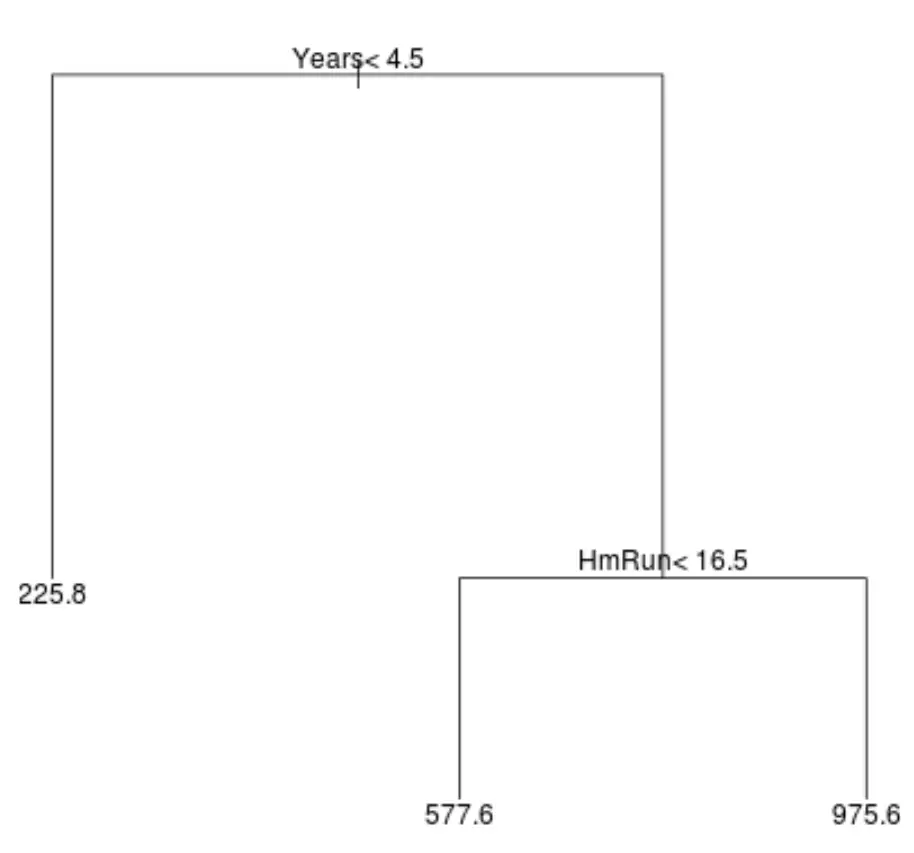
Спосіб тлумачення дерева такий:

• Гравці, які грали менше 4,5 років, мають прогнозовану зарплату в розмірі $225,8 тис.
• Гравці, які грали більше 4,5 років або більше і менше 16,5 хоум-ранів у середньому, мають прогнозовану зарплату в розмірі $577,6K.
• Очікувана зарплата гравців із стажем гри 4,5 роки та більше та в середньому 16,5 хоум-ранів становить 975,6 тисяч доларів.

Результати цієї моделі мають бути інтуїтивно зрозумілими: гравці з більшим досвідом і більшою кількістю середніх хоум-ранів, як правило, отримують вищі зарплати.

Потім ми можемо використовувати цю модель для прогнозування зарплати нового гравця.

Наприклад, припустимо, що даний гравець грав 8 років і в середньому робить 10 хоумранів на рік. Згідно з нашою моделлю, ми прогнозуємо, що річна зарплата цього гравця становить 577,6 тис. доларів США.

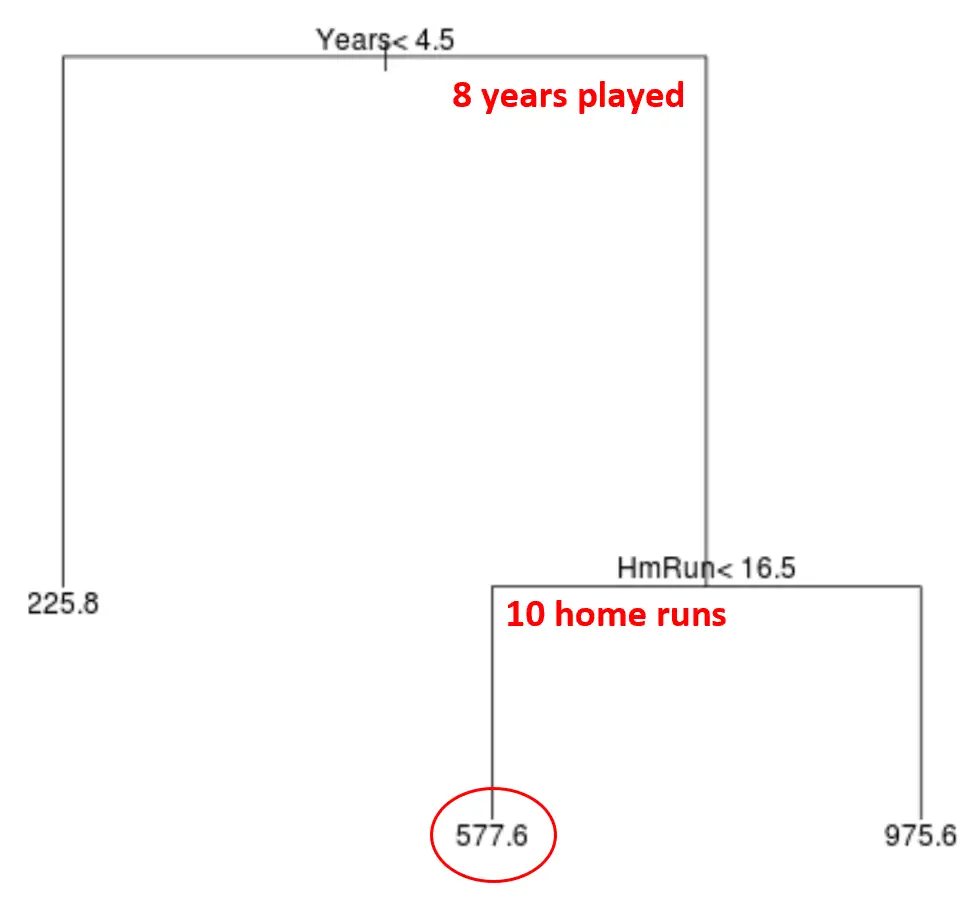
Деякі зауваження щодо дерева:

• Перша прогностична змінна, розташована у верхній частині дерева, є найважливішою, тобто тією, яка найбільше впливає на прогноз значення змінної відповіді. У цьому випадку відпрацьовані роки передбачають зарплату краще, ніж середнє по схемах .
• Ділянки в нижній частині дерева називаються листовими вузлами . Це конкретне дерево має три термінальні вузли.

Етапи створення моделей CART

Ми можемо використати такі кроки, щоб створити модель CART для заданого набору даних:

Крок 1. Використовуйте рекурсивне двійкове розбиття, щоб виростити велике дерево на навчальних даних.

По-перше, ми використовуємо жадібний алгоритм, який називається рекурсивним двійковим розщепленням, щоб виростити дерево регресії за допомогою наступного методу:

• Вважайте всі змінні предикторів X _{1 ,} X ₂ , …, залишкова стандартна помилка) найменшими. .
  • Для дерев класифікації ми вибираємо предиктор і точку відрізу так, щоб результуюче дерево мало найнижчий рівень помилок класифікації.
• Повторіть цей процес, зупиняючись лише тоді, коли кожен термінальний вузол має менше певної мінімальної кількості спостережень.

Цей алгоритм є жадібним , тому що на кожному кроці процесу побудови дерева він визначає найкраще розбиття лише на цьому кроці, замість того, щоб дивитися в майбутнє та вибирати розбиття, яке призведе до кращого глобального дерева на майбутньому етапі.

Крок 2. Застосуйте скорочення складності вартості до великого дерева, щоб отримати послідовність найкращих дерев на основі α.

Після того, як ми виростили велике дерево, нам потрібно обрізати його за допомогою методу, відомого як комплексне обрізання, який працює наступним чином:

• Для кожного можливого дерева з T кінцевими вузлами знайдіть дерево, яке мінімізує RSS + α|T|.
• Зауважте, що коли ми збільшуємо значення α, дерева з більшою кількістю кінцевих вузлів штрафуються. Це гарантує, що дерево не стане занадто складним.

Результатом цього процесу є послідовність найкращих дерев для кожного значення α.

Крок 3: використовуйте k-кратну перехресну перевірку, щоб вибрати α.

Коли ми знайдемо найкраще дерево для кожного значення α, ми можемо застосувати k-кратну перехресну перевірку, щоб вибрати значення α, яке мінімізує помилку тестування.

Крок 4: Виберіть остаточний шаблон.

Нарешті, ми вибираємо остаточну модель як ту, що відповідає обраному значенню α.

Переваги та недоліки моделей CART

Моделі CART мають такі переваги :

• Їх легко інтерпретувати.
• Їх легко пояснити.
• Їх легко візуалізувати.
• Їх можна застосовувати як до задач регресії, так і до задач класифікації .

Однак моделі CART мають наступні недоліки:

• Вони, як правило, не мають такої високої точності прогнозування, як інші нелінійні алгоритми машинного навчання. Однак шляхом кластеризації багатьох дерев рішень за допомогою таких методів, як пакетування, посилення та випадкові ліси, точність прогнозування може бути покращена.

Пов’язане: Як підігнати дерева класифікації та регресії в R