Як підібрати дерева класифікації та регресії в r

Коли зв’язок між набором змінних предикторів і змінною відповіді є лінійним, такі методи, як множинна лінійна регресія, можуть створити точні прогнозні моделі.

Однак, коли зв’язок між набором предикторів і відповіддю складніший, нелінійні методи часто можуть створювати більш точні моделі.

Одним із таких методів є дерева класифікації та регресії (CART), які використовують набір змінних прогнозів для створення дерев рішень, які передбачають значення змінної відповіді.

Якщо змінна відповіді неперервна, ми можемо побудувати дерева регресії, а якщо змінна відповіді є категоричною, ми можемо побудувати дерева класифікації.

Цей підручник пояснює, як створити дерева регресії та класифікації в R.

Приклад 1: Побудова дерева регресії в R

Для цього прикладу ми використаємо набір даних Hitters із пакету ISLR , який містить різну інформацію про 263 професійних бейсболістів.

Ми використаємо цей набір даних для побудови дерева регресії, яке використовує змінні прогнозу хоум-ранів і зіграних років для прогнозування зарплати даного гравця.

Виконайте наведені нижче кроки, щоб створити це дерево регресії.

Крок 1: Завантажте необхідні пакети.

Спочатку ми завантажимо необхідні пакети для цього прикладу:

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Крок 2: Побудуйте початкове дерево регресії.

Спочатку ми побудуємо велике початкове дерево регресії. Ми можемо гарантувати, що дерево велике, використовуючи мале значення для cp , яке означає «параметр складності».

Це означає, що ми будемо виконувати подальші розбиття на дереві регресії, доки загальний R-квадрат моделі збільшиться принаймні на значення, визначене cp.

Потім ми використаємо функцію printcp() для друку результатів моделі:

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

Крок 3: Обріжте дерево.

Далі ми обрізаємо дерево регресії, щоб знайти оптимальне значення для використання cp (параметра складності), яке призводить до найменшої помилки тесту.

Зауважте, що оптимальне значення для cp – це те, яке призводить до найменшої помилки x у попередньому виході, який представляє помилку спостережень із даних перехресної перевірки.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

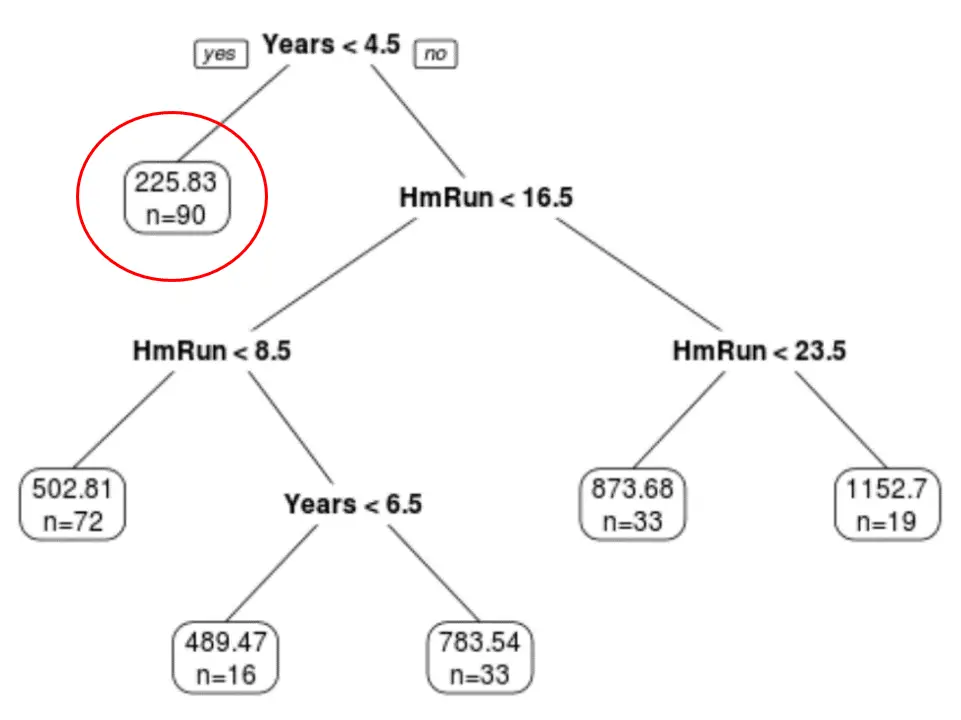
Ми бачимо, що остаточне обрізане дерево має шість кінцевих вузлів. Кожен кінцевий вузол відображає прогнозовану зарплату гравців у цьому вузлі, а також кількість спостережень із вихідного набору даних, які належать до цього класу.

Наприклад, ми бачимо, що в початковому наборі даних було 90 гравців із досвідом менше 4,5 років і їхня середня зарплата становила 225,83 тисячі доларів.

Крок 4. Використовуйте дерево для прогнозування.

Ми можемо використовувати остаточне обрізане дерево, щоб спрогнозувати зарплату певного гравця на основі його багаторічного досвіду та середнього хоумрану.

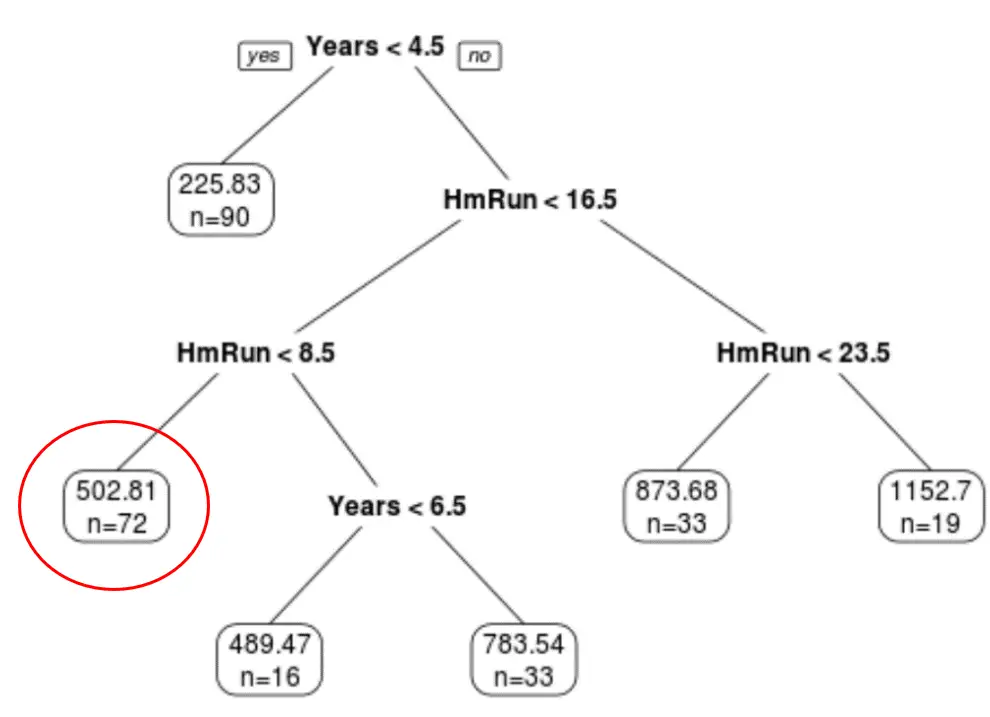
Наприклад, очікувана зарплата гравця, який має 7 років досвіду та 4 хоум-рани в середньому, становить 502,81 тис. доларів .

Ми можемо використати функцію predict() у R, щоб підтвердити це:

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

Приклад 2: Побудова дерева класифікації в R

Для цього прикладу ми використаємо набір даних ptitanic із пакета rpart.plot , який містить різноманітну інформацію про пасажирів на борту «Титаніка».

Ми використаємо цей набір даних для створення класифікаційного дерева, яке використовує змінні предикторів клас , стать і вік , щоб передбачити, чи вижив даний пасажир чи ні.

Виконайте наступні кроки, щоб створити це дерево класифікації.

Крок 1: Завантажте необхідні пакети.

Спочатку ми завантажимо необхідні пакети для цього прикладу:

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Крок 2: Побудуйте початкове дерево класифікації.

Спочатку ми побудуємо велике початкове дерево класифікації. Ми можемо гарантувати, що дерево велике, використовуючи мале значення для cp , яке означає «параметр складності».

Це означає, що ми будемо виконувати подальші розбиття на дереві класифікації до тих пір, поки загальна відповідність моделі збільшиться принаймні на значення, визначене cp.

Потім ми використаємо функцію printcp() для друку результатів моделі:

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

Крок 3: Обріжте дерево.

Далі ми обрізаємо дерево регресії, щоб знайти оптимальне значення для використання cp (параметра складності), яке призводить до найменшої помилки тесту.

Зауважте, що оптимальне значення для cp – це те, яке призводить до найменшої помилки x у попередньому виході, який представляє помилку спостережень із даних перехресної перевірки.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

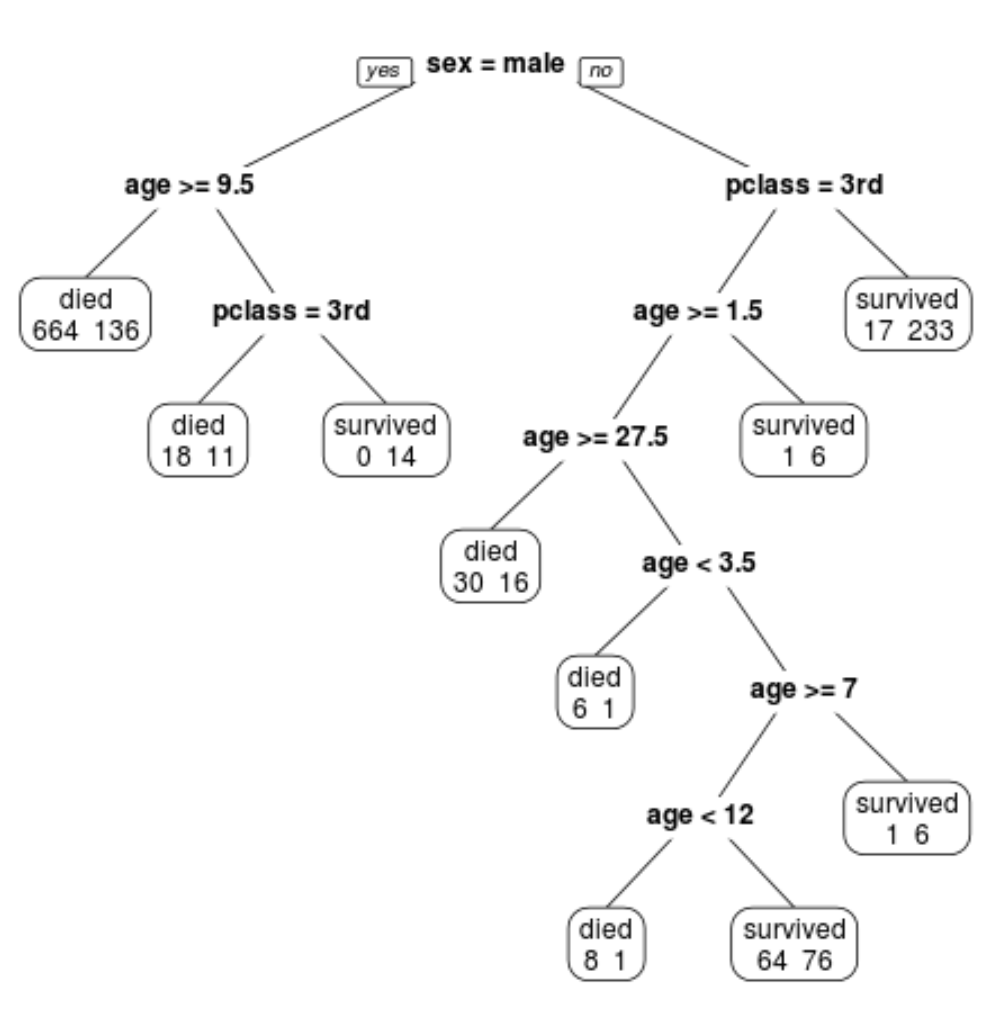
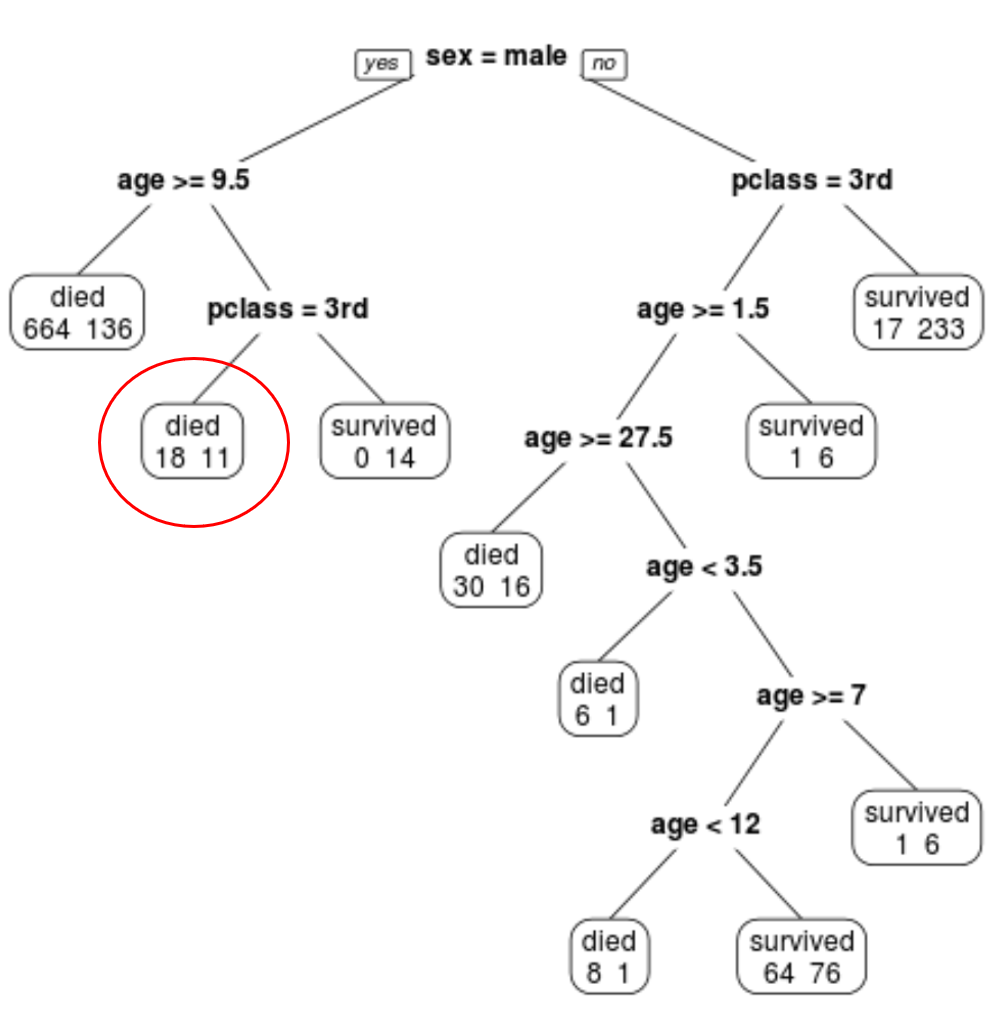
Ми бачимо, що остаточне обрізане дерево має 10 кінцевих вузлів. Кожен термінальний вузол вказує кількість загиблих пасажирів, а також кількість тих, хто вижив.

Наприклад, у крайньому лівому вузлі ми бачимо, що 664 пасажири загинули і 136 вижили.

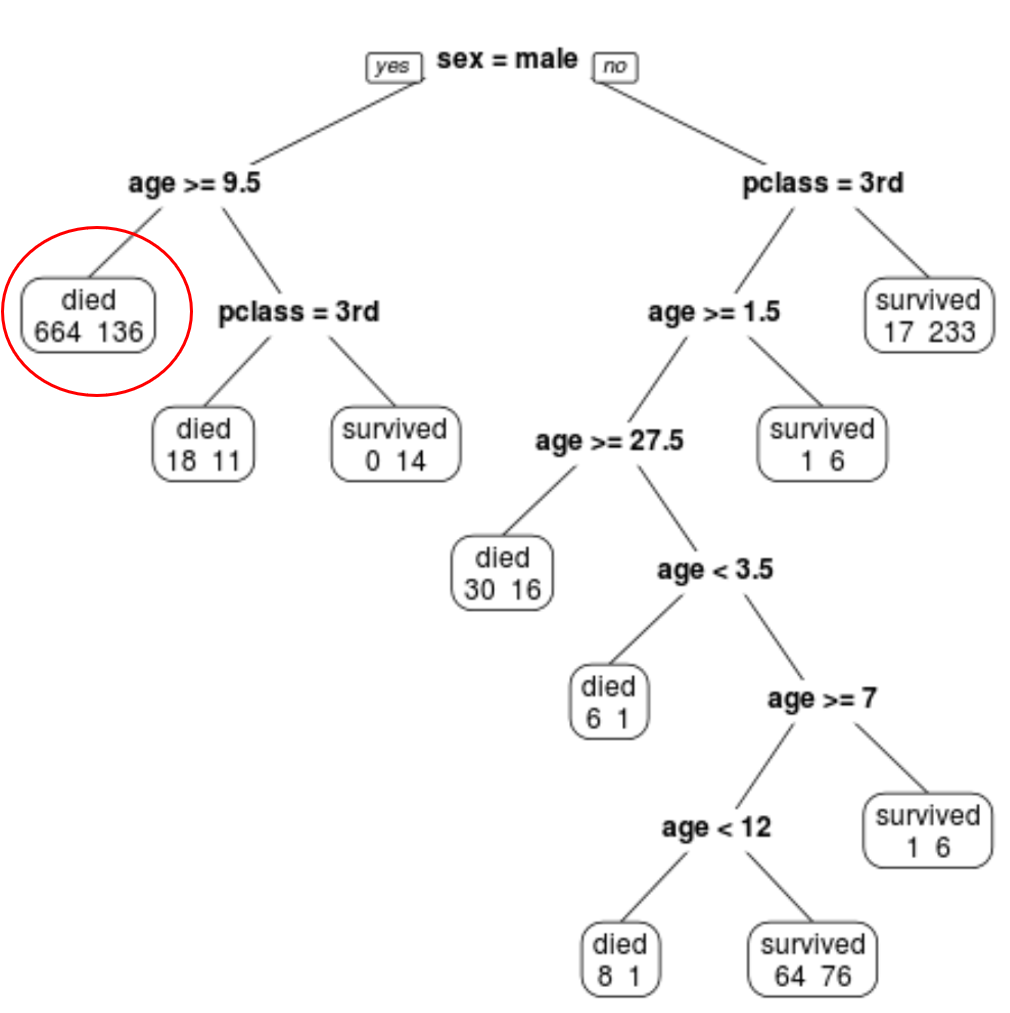
Крок 4. Використовуйте дерево для прогнозування.

Ми можемо використовувати остаточно обрізане дерево, щоб передбачити ймовірність того, що даний пасажир виживе, виходячи з його класу, віку та статі.

Наприклад, пасажир чоловічої статі у віці 8 років і в першому класі має ймовірність виживання 11/29 = 37,9%.

Повний код R, використаний у цих прикладах, можна знайти тут .