Чи може дисперсія бути негативною?

У статистиці термін дисперсія стосується того, як значення розподіляються в даному наборі даних.

Поширене запитання, яке студенти ставлять про дисперсію:

Чи може дисперсія бути негативною?

Відповідь: ні, дисперсія не може бути негативною. Найменше значення, яке воно може прийняти, дорівнює нулю.

Щоб зрозуміти, чому це так, нам потрібно зрозуміти, як насправді обчислюється дисперсія.

Як розрахувати розрив

Формула для знаходження дисперсії вибірки (позначається s ² ) має вигляд:

s ² = Σ (x _i – x ) ² / (n-1)

золото:

• x : вибірка означає
• x _i : ^i-те спостереження у вибірці
• N : Розмір вибірки
• Σ : грецький символ, що означає «сума»

Наприклад, припустімо, що ми маємо такий набір даних із 10 значеннями:

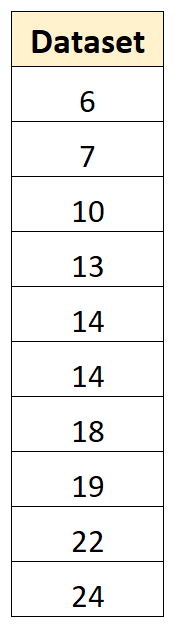
Ми можемо використати такі кроки, щоб обчислити дисперсію цієї вибірки:

Крок 1: Знайдіть середнє значення

Середнє – це просто середнє. Це виходить 14,7 .

Крок 2: Знайдіть квадрати відхилень

Тоді ми можемо обчислити квадратичне відхилення кожного окремого значення від середнього.

Наприклад, перше квадратне відхилення обчислюється як (6-14,7) ² = 75,69.

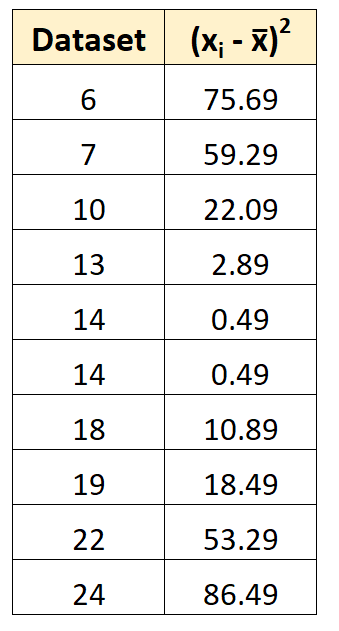
Крок 3: Знайдіть суму квадратів відхилень

Тоді ми можемо підсумувати всі квадрати відхилень:

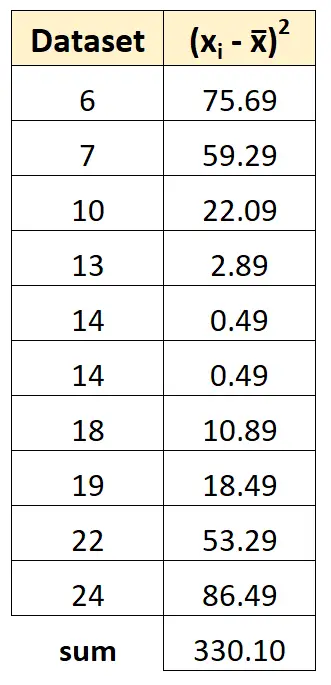
Крок 4: Обчисліть вибіркову дисперсію

Нарешті, ми можемо обчислити дисперсію вибірки як суму квадратів відхилень, поділену на (n-1):

s ² = 330,1 / (10-1) = 330,1 / 9 = 36,678

Вибіркова дисперсія виявляється 36 678 .

Приклад нульової дисперсії

Єдиний спосіб для набору даних мати нульову дисперсію – це якщо всі значення в наборі даних однакові .

Наприклад, такий набір даних має нульову дисперсію вибірки:

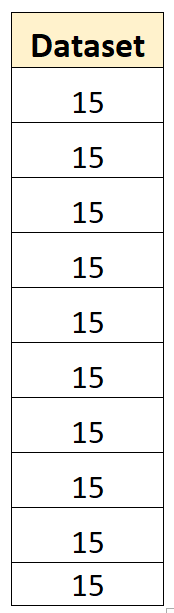
Середнє значення набору даних становить 15, і жодне з окремих значень не відхиляється від середнього. Таким чином, сума квадратів відхилень буде дорівнювати нулю, а вибіркова дисперсія просто дорівнюватиме нулю.

Чи може стандартне відхилення бути негативним?

Більш поширеним способом вимірювання розподілу значень у наборі даних є використання стандартного відхилення, яке є просто квадратним коренем із дисперсії.

Наприклад, якщо дисперсія даної вибірки дорівнює ^s2 = 36,678 , тоді стандартне відхилення (пишеться s ) обчислюється наступним чином:

s = √ ^s2 = √ 36,678 = 6,056

Оскільки ми вже знаємо, що дисперсія завжди дорівнює нулю або додатному числу, це означає, що стандартне відхилення ніколи не може бути від’ємним, оскільки квадратний корінь з нуля або додатного числа не може бути від’ємним.

Додаткові ресурси

Міри центральної тенденції: визначення та приклади
Міри дисперсії: визначення та приклади