Як інтерпретувати діагностичні графіки в r

Моделі лінійної регресії використовуються для опису зв’язку між однією або декількома змінними предиктора та змінною відповіді.

Однак після підгонки регресійної моделі доцільно створити діаграми діагностики , щоб проаналізувати залишки моделі та переконатися, що лінійна модель підходить для конкретних даних, з якими ми працюємо.

У цьому підручнику пояснюється, як створювати та інтерпретувати діаграми діагностики для даної моделі регресії в R.

Приклад: створюйте та інтерпретуйте діаграми діагностики в R

Припустімо, що ми використовуємо просту модель лінійної регресії, використовуючи «вивчені години», щоб передбачити «екзаменаційну оцінку» студентів у певному класі:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

Ми можемо використати команду plot() для створення чотирьох діагностичних графіків для цієї моделі регресії:

 #produce diagnostic plots for regression model
plot(model)

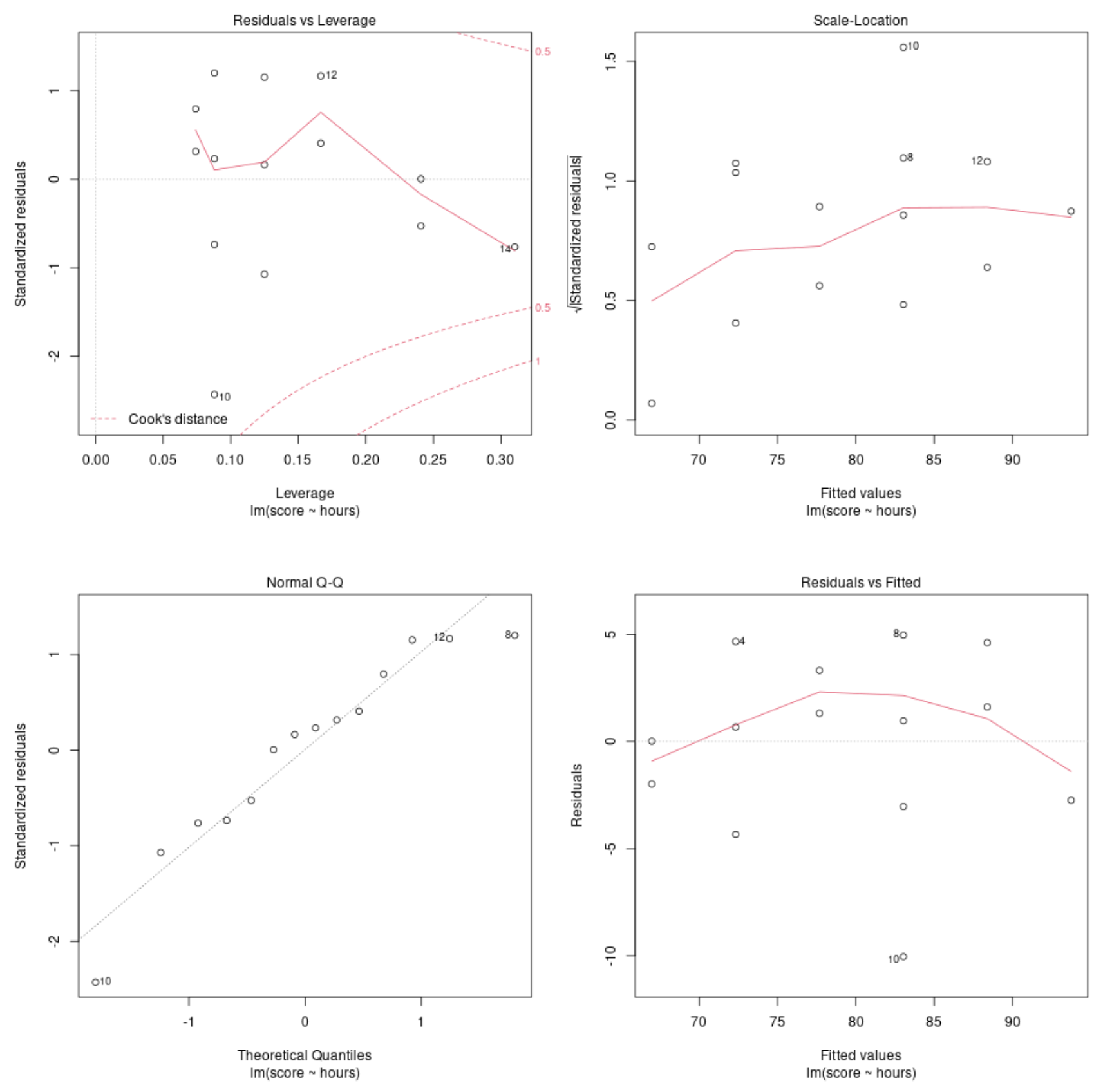
Діагностична таблиця №1: Залишки проти Діаграма кредитного плеча

Цей графік використовується для визначення впливових спостережень. Якщо будь-які точки на цьому графіку виходять за межі відстані Кука (пунктирні лінії), то це є впливовим спостереженням.

У нашому прикладі ми бачимо, що спостереження №10 є найближчим до межі відстані Кука, але воно не виходить за межі пунктирної лінії. Це означає, що в нашому наборі даних немає надто впливових точок.

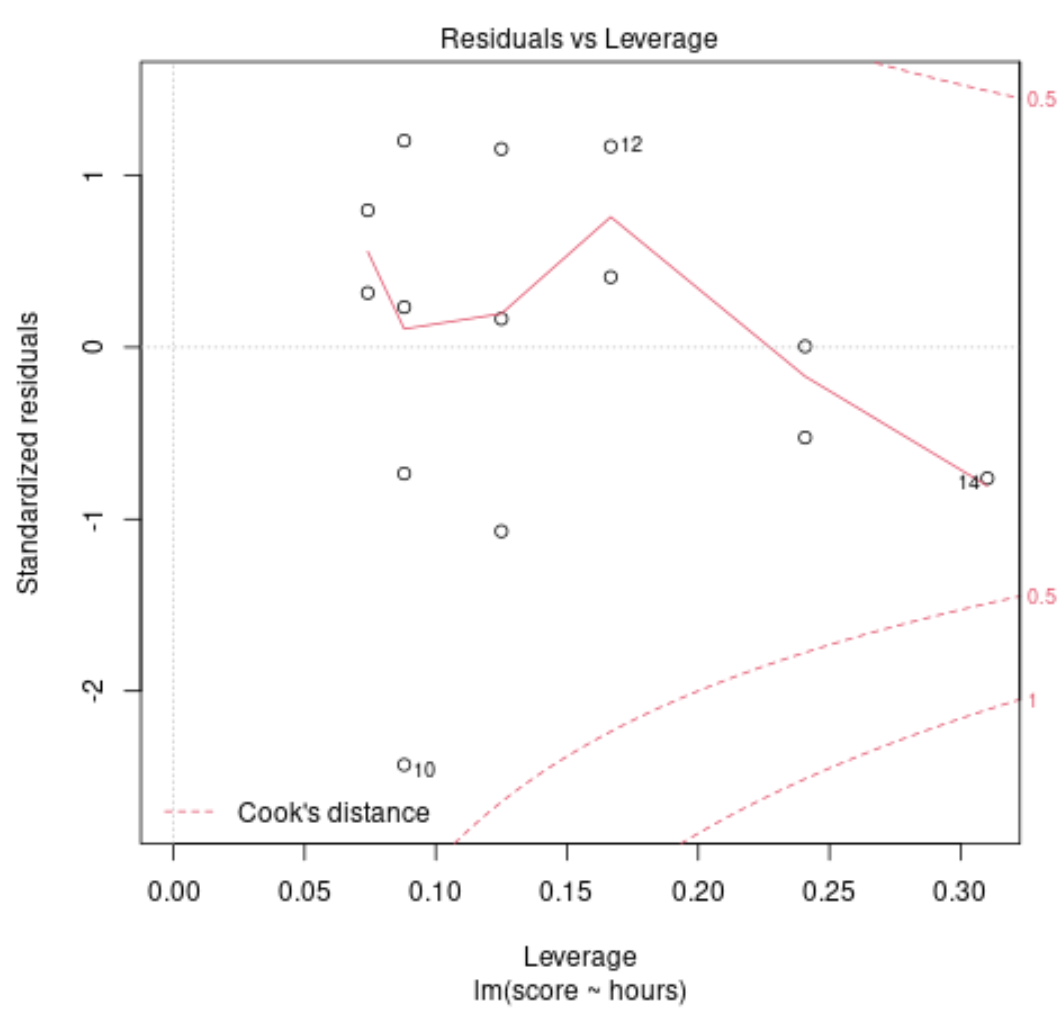
Діагностичний графік №2: графік масштабу та розташування

Цей графік використовується для перевірки припущення про рівність дисперсії (також називається «гомоскедастичністю») серед залишків нашої регресійної моделі. Якщо червона лінія розташована приблизно горизонтально на графіку, то, ймовірно, виконується припущення про однакову дисперсію.

У нашому прикладі ми бачимо, що червона лінія не зовсім горизонтальна на графіку, але вона не відхиляється занадто різко в будь-якій точці. Ймовірно, ми стверджуємо, що припущення рівної дисперсії в цьому випадку не порушується.

Пов’язане: Розуміння гетероскедастичності в регресійному аналізі

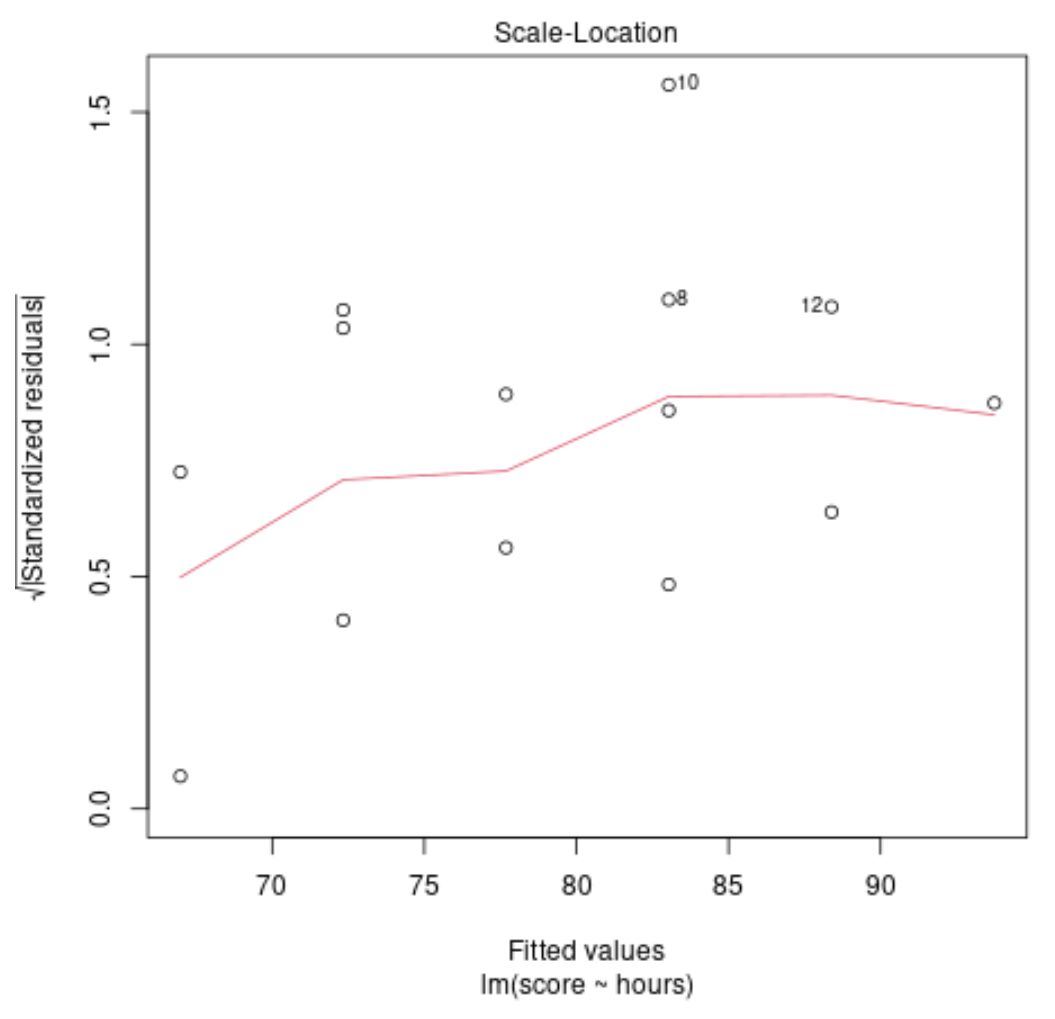
Діагностична траса №3: нормальна траса QQ

Цей графік використовується, щоб визначити, чи нормально розподілені залишки регресійної моделі. Якщо точки на цьому графіку лежать приблизно уздовж прямої діагоналі, то можна вважати, що залишки розподілені нормально.

У нашому прикладі ми бачимо, що точки лежать приблизно вздовж діагональної прямої. Спостереження №10 і №8 трохи відхиляються від лінії на кінцях, але недостатньо, щоб стверджувати, що залишки не розподілені нормально.

Діагностична схема №4: Залишки проти Скоригований сюжет

Цей графік використовується для визначення того, чи мають залишки нелінійні моделі. Якщо червона лінія в центрі графіка приблизно горизонтальна, ми можемо припустити, що залишки дотримуються лінійної моделі.

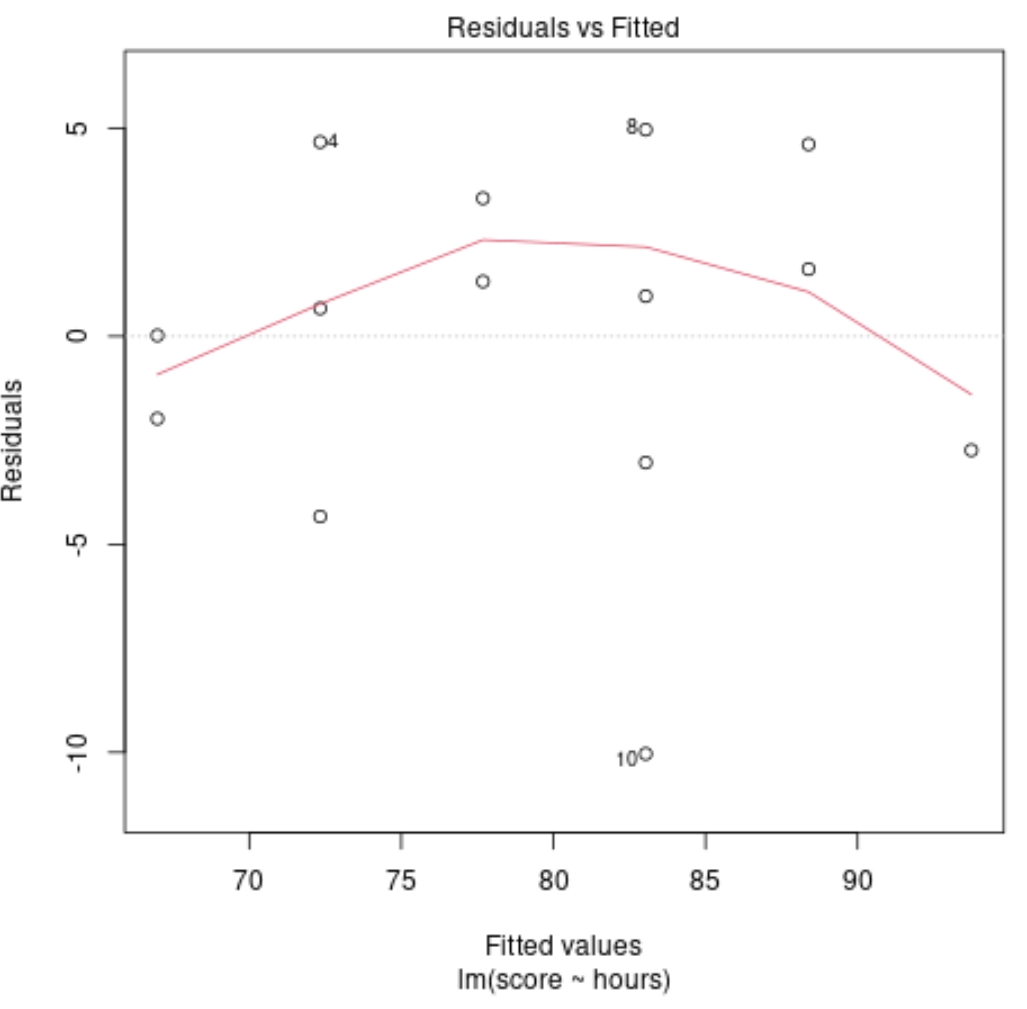
У нашому прикладі ми бачимо, що червона лінія відхиляється від ідеальної горизонтальної лінії, але незначно. Ймовірно, ми стверджуємо, що залишки дотримуються приблизно лінійної моделі і що модель лінійної регресії підходить для цього набору даних.

Додаткові ресурси

Чотири припущення лінійної регресії
Що таке залишки в статистиці?
Як створити ділянку залишків у R
Як інтерпретувати графік масштабу та розташування