Діаграма розкиду

У цій статті пояснюється, що таке діаграма розсіювання. Таким чином, ви дізнаєтеся, для чого використовується хмара точок, як створити хмару точок, як її інтерпретувати та приклади хмар точок.

Що таке хмара точок?

Діаграма розсіювання або діаграма розсіювання — це тип статистичної діаграми, у якій набір даних двох змінних зображено на двох осях декартових координат.

Тому діаграми розсіювання використовуються для аналізу зв’язку між двома статистичними змінними.

Діаграма розсіювання має кілька різних назв, наприклад кореляційна діаграма або діаграма розсіювання .

Слід зазначити, що точкова діаграма вважається одним із основних інструментів контролю якості, як і діаграма Парето, діаграма причин і наслідків, блок-схема тощо.

Як зробити точкову діаграму

Щоб створити точкову діаграму, потрібно виконати наступні кроки:

1. Зберіть статистичні дані із зразка, який ви хочете проаналізувати. Майте на увазі, що для створення діаграми розсіювання має бути принаймні дві кількісні змінні.
2. Побудуйте дві осі діаграми розсіювання.
3. Визначте дві статистичні змінні, які будуть зображені на графіку.
4. Відкалібруйте масштаб кожної осі графіка. Для цього рекомендується спочатку знайти мінімум і максимум кожної змінної і на основі цих значень масштабувати кожну вісь.
5. Позначте кожну пару даних на діаграмі розсіювання точкою.
6. Проаналізуйте та інтерпретуйте отриману діаграму розсіювання.

Приклад діаграми розсіювання

Ознайомившись із визначенням діаграми розсіювання та теорією її створення, цей розділ представляє діаграму цього типу як приклад.

• У наведеній нижче частотній таблиці як дані були зібрані бали з математики та статистики вибірки з 20 студентів. Побудуйте набір даних на діаграмі розсіювання та проаналізуйте його.

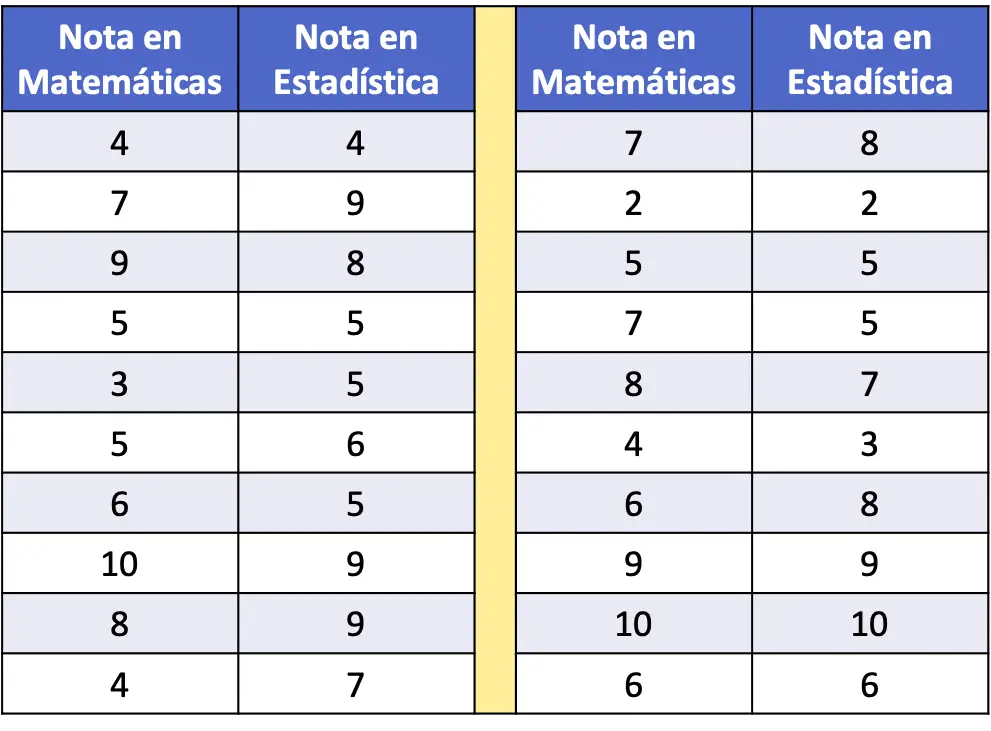
Щоб представити ряд даних на точковій діаграмі, нам просто потрібно побудувати дві осі, відкалібрувати їх і нанести точку на графіку для кожної пари даних. Пам’ятайте, що точка на графіку розміщується на перетині уявних ліній, що відповідають кожному його значенню.

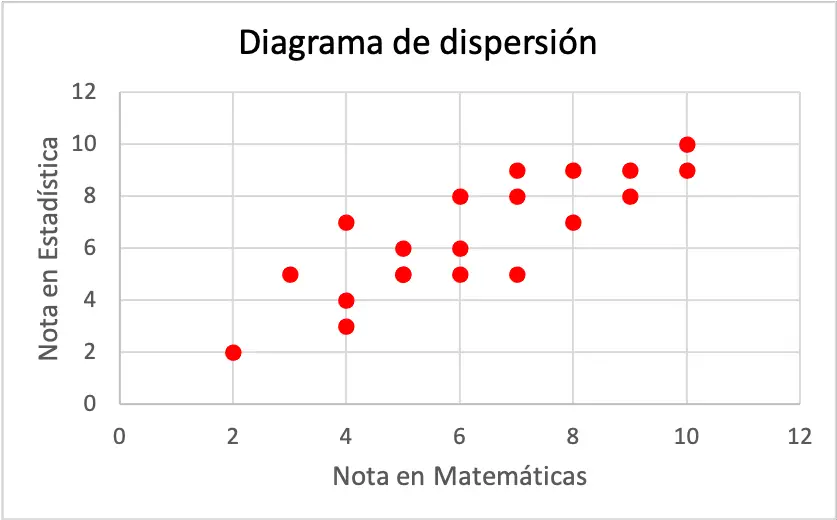
Кожна вісь діаграми розсіювання представляє змінну. Точніше, горизонтальна вісь відповідає оцінці, отриманій з математики, а з іншого боку, вертикальна вісь відповідає оцінці, отриманій зі статистики.

Як ви можете бачити з діаграми розсіювання, дві змінні мають позитивну кореляцію, оскільки одна змінна збільшується разом із збільшенням іншої змінної. Тому робиться висновок, що якщо учень отримує кращу оцінку з математики, то ймовірніше, що він також отримає кращу оцінку зі статистики, і навпаки.

Однак попередній висновок не означає, що одна змінна є причиною іншої, тому що отримання хорошої оцінки з математики не гарантує автоматично хорошу оцінку зі статистики без будь-яких дій, а краще вивчати обидва предмети. У наступному розділі ми розглянемо цю концепцію більш детально.

Діаграма розсіювання та кореляція

За допомогою діаграми розсіювання можна визначити тип кореляції між двома змінними:

• Пряма кореляція (або позитивна кореляція) : одна змінна збільшується, коли інша також збільшується.
• Зворотна кореляція (або негативна кореляція) : коли одна змінна зростає, інша зменшується, і навпаки, якщо одна змінна зменшується, інша збільшується.
• Нульова кореляція (кореляція відсутня) : між двома змінними немає зв’язку.

Подібним чином, незалежно від того, чи є кореляція між двома змінними прямою чи зворотною, кореляцію також можна класифікувати на основі сили чи слабкості зв’язку між двома змінними.

• Сильна кореляція: дві змінні тісно пов’язані. Точки об’єднуються на хмарі точок. Це полегшує визначення зв’язку між змінними.
• Низька кореляція : між двома змінними існує зв’язок, але його важко визначити. На хмарі точок точки розташовані далеко одна від одної.

З іншого боку, кореляцію також можна обчислити чисельно за допомогою формули, що дає змогу математично визначити, наскільки тісно пов’язані дві різні змінні. Щоб побачити, як це працює, натисніть таке посилання:

Пам’ятайте, що навіть якщо існує кореляція між двома змінними, це не означає, що між ними існує причинно-наслідковий зв’язок, тобто кореляція між двома змінними не означає, що зміна однієї змінної є причиною зміни іншої. змінна.

Отже, як і на діаграмі розсіювання в попередньому розділі, хоча існує позитивна кореляція між оцінкою з математики та оцінкою зі статистики, отримати хорошу оцінку з математики не означає отримати хорошу оцінку зі статистики, тому що якщо ви вивчаєте лише математику, ви точно зазнаєте невдачі в статистиці. Отже, ці дві змінні пов’язані, але не є причиною та наслідком.

Щоб дізнатися більше, ви можете продовжити наступну публікацію:

Переваги та недоліки хмари точок

Завдяки характеристикам діаграми розсіювання цей тип статистичної діаграми має переваги та недоліки.

Перевага:

• Досить просто представити ряд даних на точковій діаграмі.
• Діаграма розсіювання дає змогу візуально проаналізувати зв’язок між двома змінними, що полегшує висновки.
• Діаграми розсіювання також можна використовувати в поглибленому статистичному дослідженні як попередній аналіз даних.

Недоліки:

• Ці типи діаграм не є корисними для представлення якісних змінних.
• Інтерпретація діаграми розсіювання може призвести до помилкового висновку про причину та наслідок між двома змінними.
• Діаграма розсіювання не дозволяє аналізувати зв’язок між більш ніж двома змінними.