Експоненціальна регресія в r (крок за кроком)

Експоненціальна регресія – це тип регресії, який можна використовувати для моделювання таких ситуацій:

1. Експоненціальне зростання: Зростання починається повільно, а потім швидко й безмежно прискорюється.

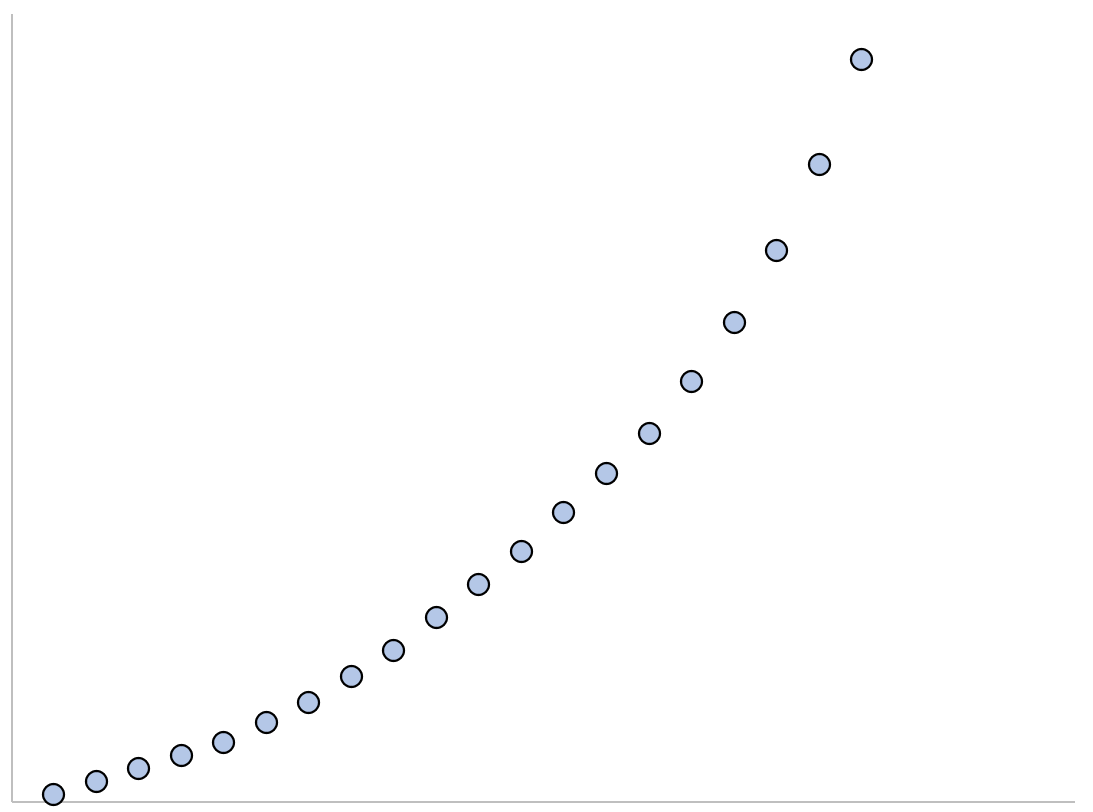
2. Експоненціальний розпад: розпад починається швидко, а потім сповільнюється, наближаючись до нуля.

Рівняння для моделі експоненціальної регресії має такий вигляд:

y = ab ^x

золото:

• y: змінна відповіді
• x: передбачувана змінна
• a, b: коефіцієнти регресії, які описують зв’язок між x і y

Наступний покроковий приклад показує, як виконати експоненціальну регресію в R.

Крок 1: Створіть дані

Спочатку давайте створимо фальшиві дані для двох змінних: x і y :

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

Крок 2: Візуалізуйте дані

Далі створимо швидку діаграму розсіювання, щоб візуалізувати зв’язок між x і y :

 plot(x, y) 

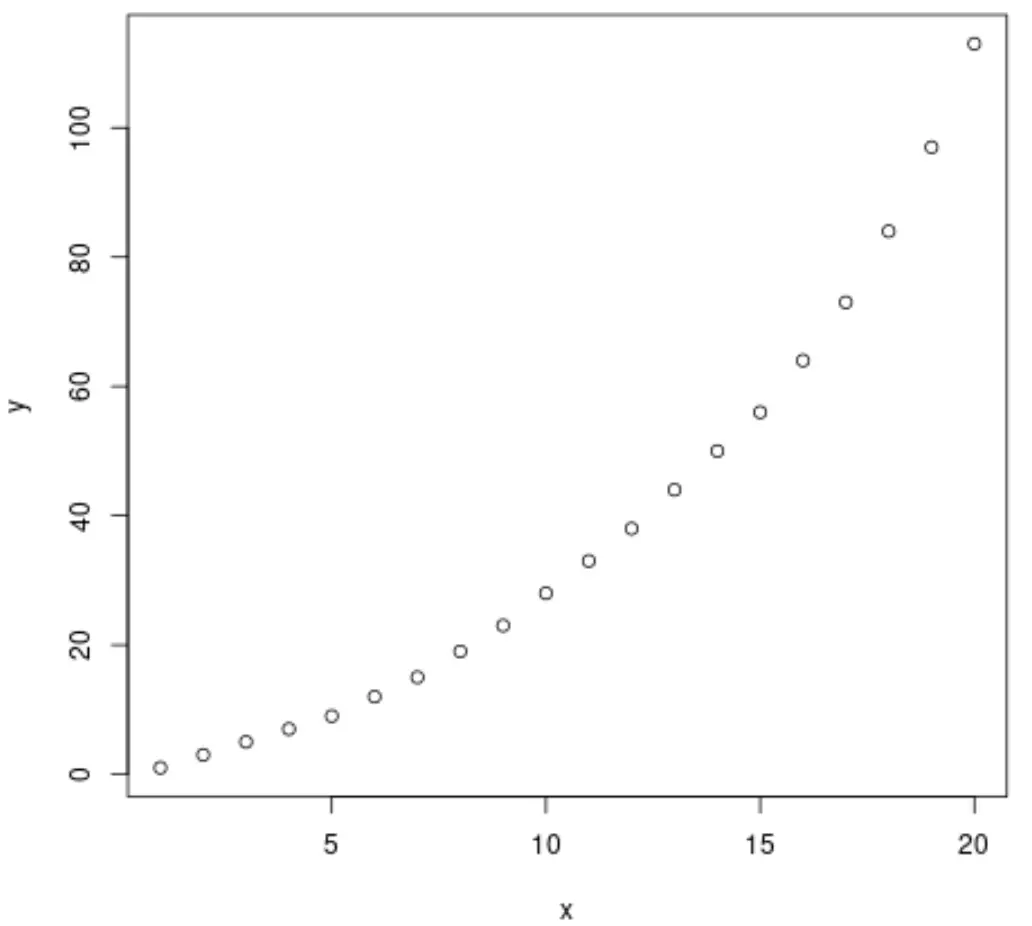
З графіка ми бачимо, що існує чітка модель експоненціального зростання між двома змінними.

Тому здається доцільним застосувати рівняння експоненціальної регресії для опису зв’язку між змінними.

Крок 3. Підберіть модель експоненціальної регресії

Далі ми використаємо функцію lm() , щоб підібрати модель експоненціальної регресії, використовуючи натуральний логарифм y як змінну відповіді та x як змінну предиктора:

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

Загальне F-значення моделі становить 204, а відповідне p-значення надзвичайно низьке (2,917e-11), що вказує на те, що модель в цілому корисна.

Використовуючи коефіцієнти з вихідної таблиці, ми можемо побачити, що підігнане рівняння експоненціальної регресії має вигляд:

ln(y) = 0,9817 + 0,2041(x)

Застосовуючи e до обох сторін, ми можемо переписати рівняння так:

y = 2,6689 * ^1,2264x

Ми можемо використати це рівняння для прогнозування змінної відповіді y на основі значення змінної предиктора x . Наприклад, якщо x = 12, ми передбачимо, що y буде 30,897 :

y = 2,6689 * 1,2264 ¹² = 30,897

Бонус: не соромтеся використовувати цей онлайн-калькулятор експоненціальної регресії, щоб автоматично обчислити рівняння експоненціальної регресії для заданого предиктора та змінної відповіді.

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як виконати квадратичну регресію в R
Як виконати поліноміальну регресію в R