Як розрахувати коефіцієнт інфляції дисперсії (vif) у sas
У регресійному аналізі мультиколінеарність виникає, коли дві або більше змінних предикторів сильно корельовані одна з одною, так що вони не надають унікальної чи незалежної інформації в моделі регресії.
Якщо ступінь кореляції між змінними досить високий, це може спричинити проблеми під час підгонки та інтерпретації регресійної моделі.
Одним із способів виявити мультиколінеарність є використання метрики, відомої як коефіцієнт інфляції дисперсії (VIF) , який вимірює кореляцію та силу кореляції між пояснювальними змінними в регресійній моделі .
Цей підручник пояснює, як обчислити VIF у SAS.
Приклад: розрахунок VIF у SAS
Для цього прикладу ми створимо набір даних, який описує атрибути 10 баскетболістів:
/*create dataset*/ data my_data; input rating points assists rebounds; datalines ; 90 25 5 11 85 20 7 8 82 14 7 10 88 16 8 6 94 27 5 6 90 20 7 9 76 12 6 6 75 15 9 10 87 14 9 10 86 19 5 7 ; run ; /*view dataset*/ proc print data =my_data;
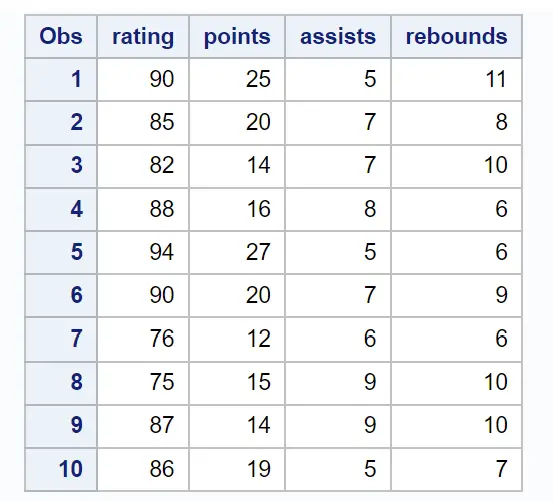
Припустімо, ми хочемо підібрати модель множинної лінійної регресії, використовуючи оцінку як змінну відповіді та очки , передачі та підбирання як змінні прогнозу.
Ми можемо використовувати PROC REG , щоб відповідати цій регресійній моделі з опцією VIF , щоб обчислити значення VIF для кожної змінної предиктора в моделі:
/*fit regression model and calculate VIF values*/ proc reg data =my_data; model rating = points assists rebounds / lively ; run ;
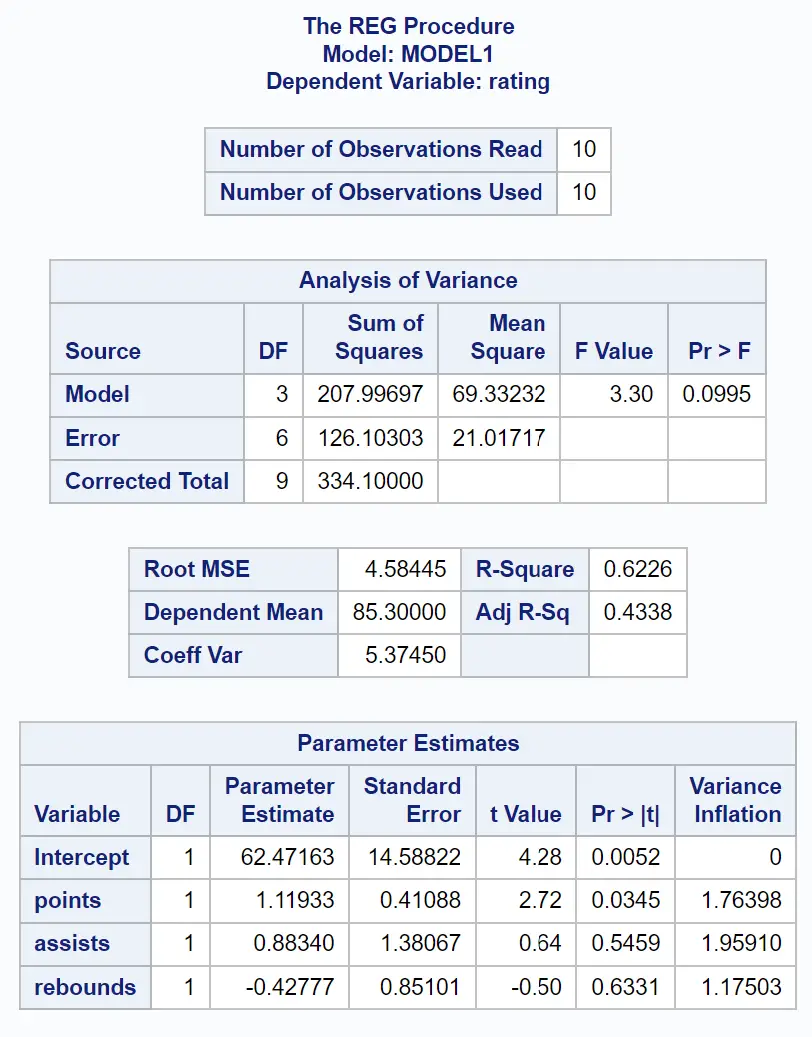
З таблиці оцінок параметрів ми можемо побачити значення VIF для кожної зі змінних предиктора:
- бали: 1,76398
- передачі: 1,96591
- підбирання: 1.17503
Примітка. Ігноруйте VIF для «Перехоплення» в шаблоні, оскільки це значення не має значення.
Значення VIF починається з 1 і не має верхньої межі. Загальне правило інтерпретації VIF:
- Значення 1 вказує на відсутність кореляції між даною змінною предиктора та будь-якою іншою змінною предиктора в моделі.
- Значення від 1 до 5 вказує на помірну кореляцію між даною змінною предиктором та іншими змінними предиктора в моделі, але часто вона недостатньо серйозна, щоб вимагати особливої уваги.
- Значення більше 5 вказує на потенційно серйозну кореляцію між даною змінною предиктора та іншими змінними предиктора в моделі. У цьому випадку оцінки коефіцієнтів і p-значення в результатах регресії, ймовірно, ненадійні.
Оскільки кожне зі значень VIF прогностичних змінних у нашій моделі регресії близьке до 1, мультиколінеарність не є проблемою в нашому прикладі.
Як боротися з мультиколінеарністю
Якщо ви визначите, що мультиколінеарність є проблемою у вашій моделі регресії, існує кілька поширених способів її вирішення:
1. Видаліть одну або кілька сильно корельованих змінних.
Це найшвидше рішення в більшості випадків і часто є прийнятним рішенням, оскільки змінні, які ви видаляєте, все одно є зайвими та додають мало унікальної чи незалежної інформації до моделі.
2. Лінійно поєднує змінні предикторів певним чином, наприклад, додаючи або віднімаючи їх певним чином.
Таким чином ви можете створити нову змінну, яка охоплює інформацію з обох змінних, і у вас більше не буде проблеми мультиколінеарності.
3. Виконайте аналіз, призначений для врахування сильно корельованих змінних, таких як аналіз головних компонентів або регресія часткових найменших квадратів (PLS).
Ці методи спеціально розроблені для роботи з висококорельованими змінними предикторів.
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати інші типові завдання в SAS:
Як виконати множинну лінійну регресію в SAS
Як створити ділянку залишку в SAS
Як розрахувати відстань приготування в SAS