Операції над множинами: об'єднання, перетин, доповнення та різниця

Набір – це сукупність елементів.

Позначаємо множину великою літерою, а елементи множини визначаємо за допомогою фігурних дужок. Наприклад, припустимо, що ми маємо множину під назвою “A” з елементами 1, 2, 3. Ми б записали це так:

A = {1, 2, 3}

Цей підручник пояснює найпоширеніші операції з множинами в ймовірності та статистиці.

спілка

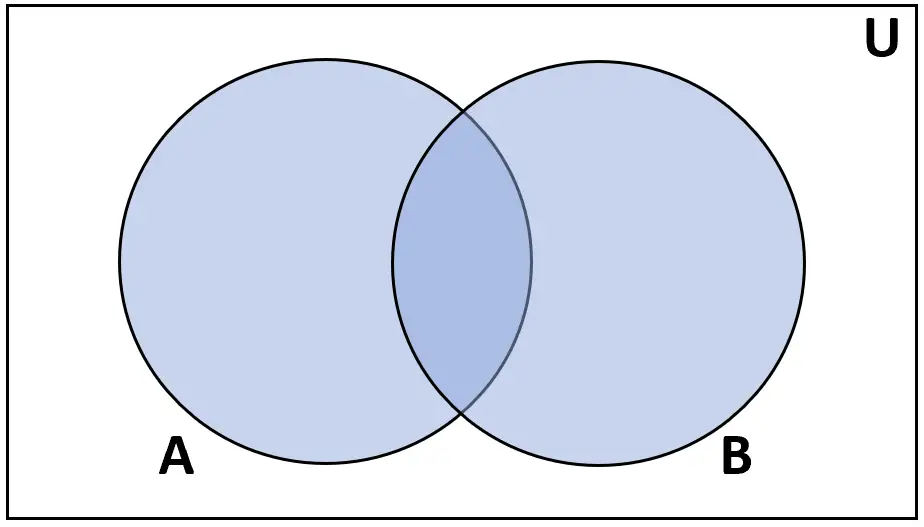
Визначення: об’єднання множин A і B — це множина елементів, що знаходяться або в A, або в B.

Рейтинг: A ∪ B

приклади:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Перетин

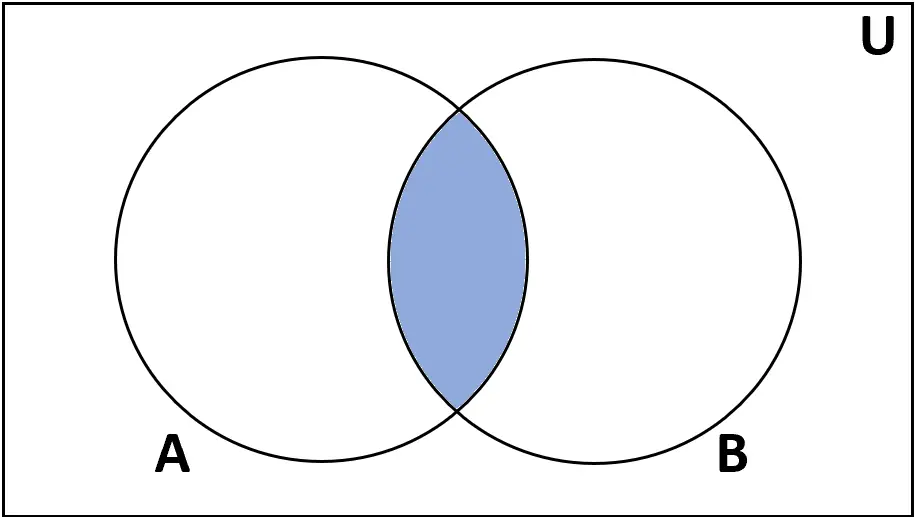
Визначення: Перетин множин A і B — це множина елементів, які містяться в A і B.

Позначення: A ∩ B

приклади:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Доповнюють

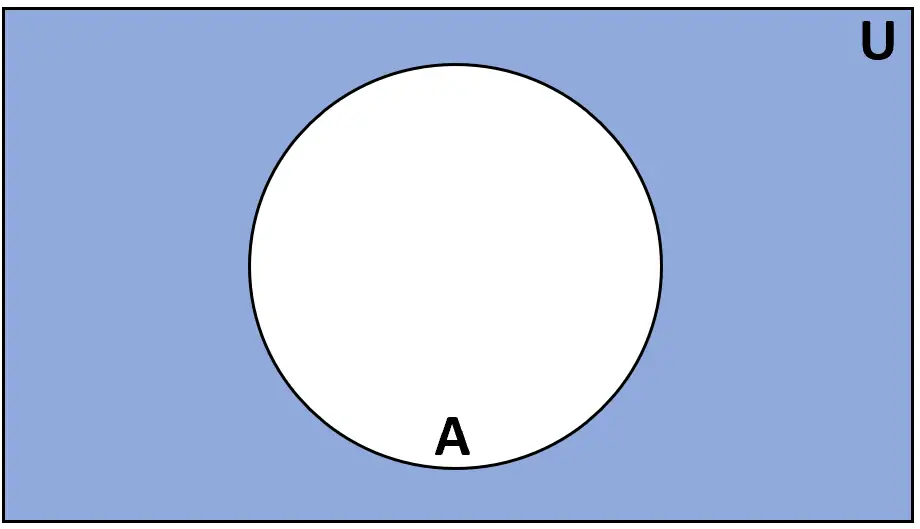
Визначення: Доповненням до множини A є множина елементів, які входять до універсальної множини U, але не входять до A.

Рейтинг: A’ або ^Ac

приклади:

• Якщо U = {1, 2, 3, 4, 5, 6} і A = {1, 2}, то A ^c = {3, 4, 5, 6}
• Якщо U = {1, 2, 3} і A = {1, 2}, то A ^c = {3}

Різниця

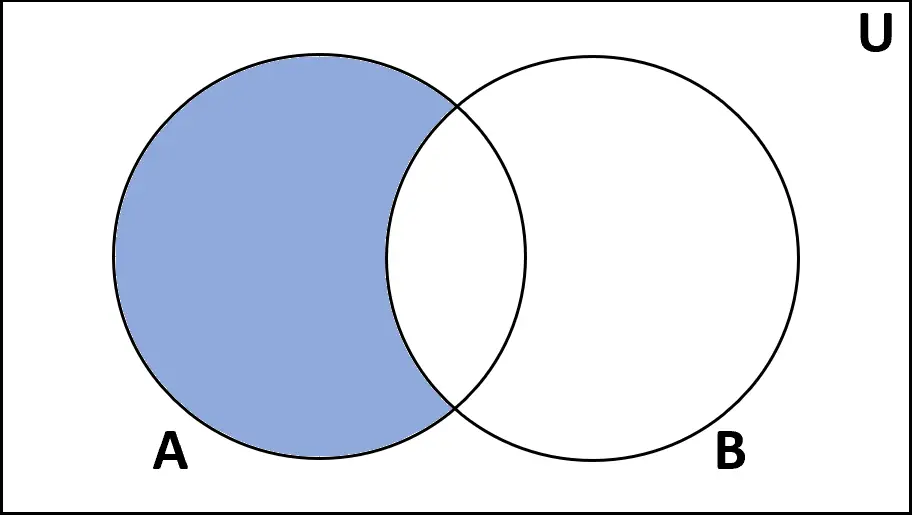
Визначення: різниця між множинами A і B – це множина елементів, які знаходяться в A, але не в B.

Оцінки: A–B

приклади:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Симетрична різниця

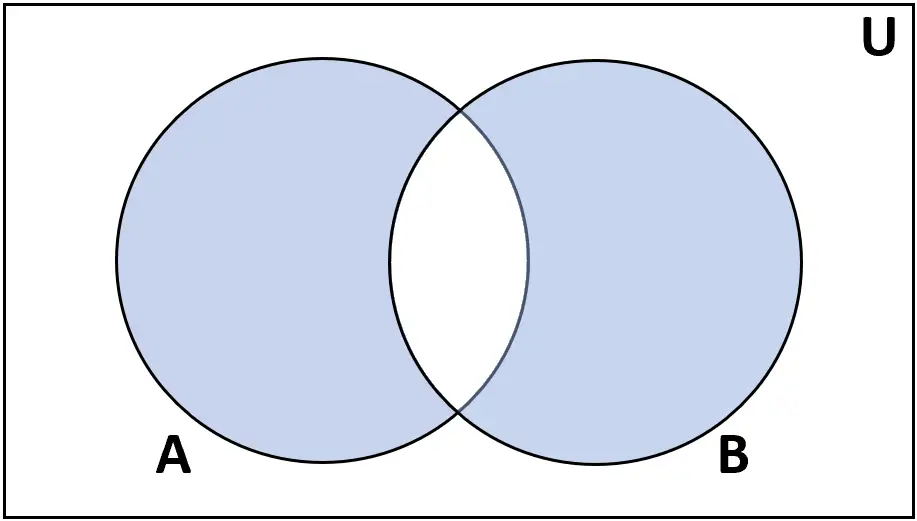
Визначення: Симетрична різниця множин A і B — це множина елементів, які знаходяться в A або B, але не в обох.

Рейтинг: AΔB

приклади:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

Декартовий добуток

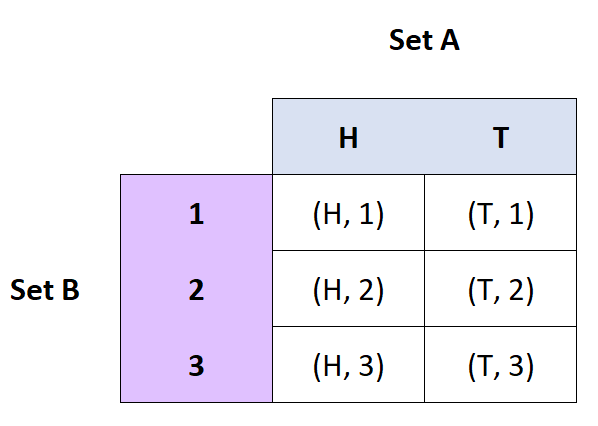
Визначення: декартів добуток множин A і B — це множина впорядкованих пар A і B.

Рейтинг: A x B

приклади:

• Якщо A = {H, T} і B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
• Якщо A = {T, H} і B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}