Закон бенфорда

за Редакція 3 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке закон Бенфорда. Крім того, ви зможете побачити, як був відкритий закон Бенфорда та які застосування цього статистичного закону.

Що таке закон Бенфорда?

Закон Бенфорда , також званий законом першої цифри , — це статистичний закон, згідно з яким ймовірність того, що перша цифра фрагмента даних дорівнює 1, більша, ніж ймовірність того, що це інше число.

Іншими словами, закон Бенфорда говорить, що в наборі числових даних, які існують у реальному житті, число 1 є найбільш повторюваним числом як перша цифра даних.

Крім того, чим вище число, тим менша ймовірність того, що він опиниться на першому місці. Отже, перше число швидше 1, ніж 2, але 2 швидше, ніж 3, 3 швидше, ніж 4 і так далі.

Своєю назвою закон Бенфорда зобов’язаний американцеві Френку Бенфорду. Хоча Бенфорд не винайшов його, він популяризував це статистичне правило. Нижче ми побачимо походження закону Бенфорда.

Формула закону Бенфорда

Закон Бенфорда стверджує, що ймовірність того, що перша цифра є певним числом, дорівнює логарифму один плюс один над цим числом.

Таким чином , формула закону Бенфорда виглядає так:

$\begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}$

Отже, з формули закону Бенфорда ми можемо вивести ймовірність того, що для кожного числа воно є першою цифрою елемента даних. У наступній таблиці ви можете побачити відсотки всіх ймовірностей:

малюнок	Ймовірність, що бути першим номером
1	30,1%
2	17,6%
3	12,5%
4	9,7%
5	7,9%
6	6,7%
7	5,8%
8	5,1%
9	4,6%

Крім того, нижче ви можете побачити гістограму, на якій графічно представлені всі ймовірності закону Бенфорда:

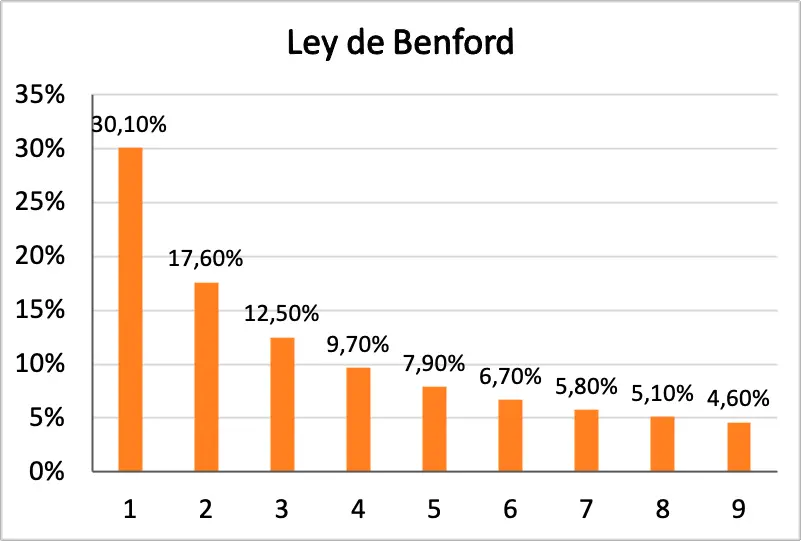
Історія закону Бенфорда

У 1881 році математик Саймон Ньюкомб вивів закон Бенфорда, коли виявив, що перші сторінки таблиць логарифмів використовувалися значно частіше, ніж останні сторінки. Це означало, що перші цифри чисел не однаково ймовірні, але що 1 зустрічалася частіше, ніж 2, 2 частіше, ніж 3, і так далі аж до 9.

Однак Ньюком не залишив статистичних доказів дотримання цього правила, він просто зробив вирахування з зносу логарифмічних таблиць.

Пізніше, зокрема в 1938 році, фізик Френк Бенфорд зробив таке ж спостереження, а також провів експеримент, щоб перевірити це емпірично. На наборі статистичних даних із 20 229 значень із 20 різних зразків він провів дослідження першої цифри кожного з даних. Отже, на основі результатів він продемонстрував, що закон Бенфорда виконується, і вивів формулу, яка дозволила йому обчислити ймовірність того, що перша цифра буде певним числом (ми бачили цю формулу вище).

Коротше кажучи, хоча закон Бенфорда вперше відкрив Саймон Ньюкомб, він названий на честь Френка Бенфорда, оскільки він підтвердив цей статистичний закон.

Застосування закону Бенфорда

Закон Бенфорда — статистичний закон, який знаходить застосування в дуже різних сферах. Наприклад, закон Бенфорда широко використовується в економіці, біології і навіть політиці.

В економіці закон Бенфорда часто використовується для виявлення маніпулювання даними, тому що якщо набір даних не відповідає закону Бенфорда, це вказує на те, що даними було маніпулювано. Цей закон, наприклад, використовується для виявлення можливих випадків податкового шахрайства.

Слід зазначити, що закон Бенфорда не використовується для демонстрації істинності випадкових явищ, оскільки результати рівноймовірні. Таким чином, правило Бенфорда не можна використовувати для перевірки результатів лотереї.

З іншого боку, у генетиці закон Бенфорда можна використовувати для аналізу відмінностей у довжині геному між різними типами організмів.

Нарешті, також робилися спроби виявити шахрайство виборців шляхом застосування закону Бенфорда, хоча його корисність у цьому випадку була під сумнівом.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше