Закон великих чисел: визначення + приклади

Закон великих чисел стверджує, що зі збільшенням розміру вибірки вибіркове середнє наближається до очікуваного значення.

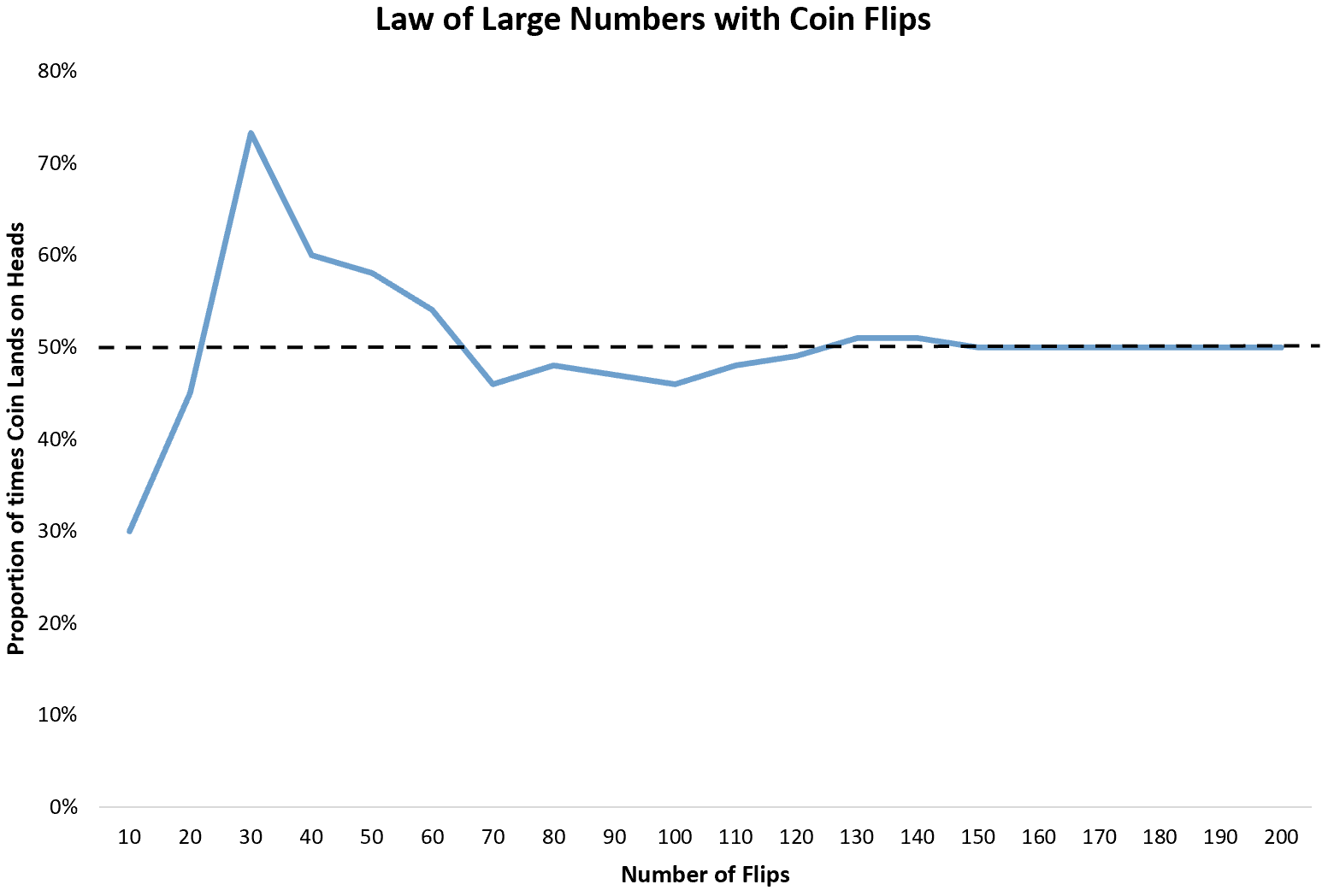
Найпростіший приклад — підкидання монети. Щоразу, коли ми підкидаємо монету, ймовірність того, що вона випаде оллами, становить 1/2. Отже, очікувана частка голів, які з’являться під час нескінченної кількості кидків, становить 1/2 або 0,5 .

Однак якщо ми підкидаємо монету 10 разів, ми можемо виявити, що вона потрапляє головами лише 3 рази. Оскільки 10 переворотів — це малий розмір вибірки, немає гарантії, що частка голови буде близькою до 0,5 .

Якщо ми продовжимо кидати монету ще 10 разів, ми можемо виявити, що вона потрапляє на голову в цілому 9 разів із 20. Якщо ми кидаємо її ще 10 разів, ми можемо виявити, що вона потрапляє на голову 22 рази з 30.

Коли ми підкидаємо монету, кількість разів, коли вона випадає, буде зближуватися до очікуваної частки 0,5 .

Ця проста ідея закону великих чисел використовується багатьма типами підприємств і галузей у реальному житті.

Закон великих чисел в казино

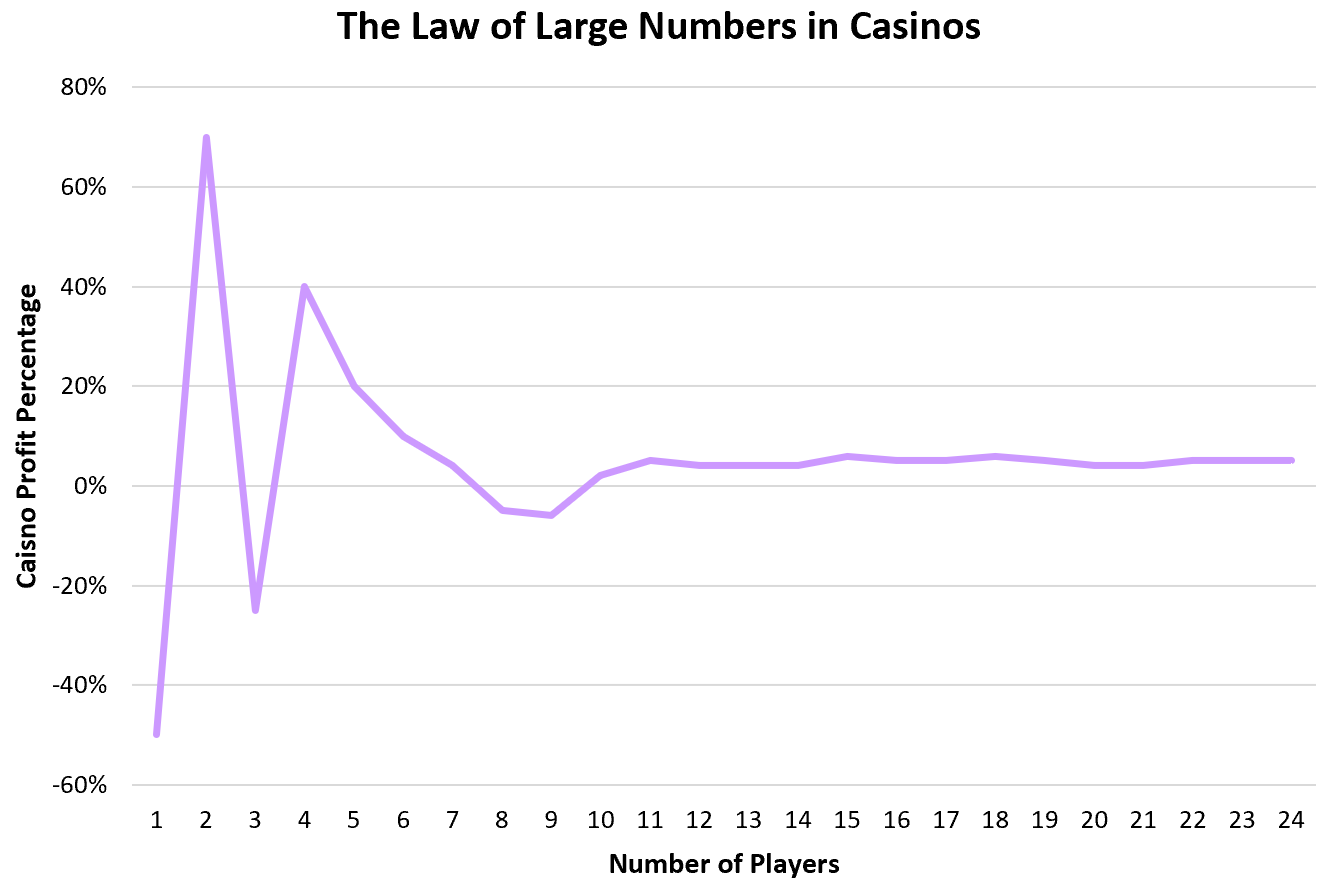
Казино покладаються на закон великих чисел для надійного отримання прибутку. У більшості ігор казино виграє приблизно в 51-55% випадків. Це означає, що окремим особам може пощастити і час від часу вони виграють пристойну суму, але з десятків тисяч окремих гравців казино виграє очікувані 51-55% часу.

Наприклад, Джессіка може зіграти кілька ігор у казино й виграти 50 доларів.

Майк також міг зіграти кілька ігор і програти 70 доларів.

Джон міг зіграти кілька ігор і виграти 25 доларів.

Сьюзен могла зіграти кілька ігор і втратити 40 доларів.

Деякі гравці виграють гроші, а інші програють гроші, але через те, як розроблено ігри, казино можуть бути впевнені, що вони виграють із тисяч осіб.

Закон великих чисел у страхуванні

Страхові компанії також покладаються на закон великих чисел, щоб залишатися прибутковими.

Основна ідея полягає в тому, що тисячі страхових компаній можуть застрахувати людей, які сплачують певну премію щомісяця, і що лише невеликий відсоток людей, яких вони страхують, насправді потребуватиме страхування для оплати великих несподіваних витрат.

Наприклад, кожна з 1000 осіб могла б платити по 1000 доларів на рік за страхування, що принесло б страховій компанії прибуток у 1 000 000 доларів.

Проте 90 особам може знадобитися отримати по 10 000 доларів США від страхової компанії, щоб покрити непередбачені витрати, пов’язані з різними нещасними випадками, що призведе до збитків у 900 000 доларів для страхової компанії.

Зрештою страхова компанія отримує прибуток у розмірі $1 000 000 – $900 000 = $100 000 .

Це означає, що страхова компанія може розраховувати на отримання досить прогнозованого прибутку в середньому на тисячах людей.

Зауважте, що ця економічна модель працює, оскільки страхова компанія страхує велику кількість людей . Якби вони застрахували лише 10 осіб, це було б надто ризиковано, оскільки великі несподівані витрати могли б знищити бізнес.

Таким чином, страхові компанії покладаються на закон великих чисел, щоб прогнозувати свої прибутки передбачуваним чином.

Закон великих чисел у відновлюваних джерелах енергії

Закон великих чисел також використовується компаніями, які займаються відновлюваною енергетикою.

Основна ідея полягає в тому, що вітрові турбіни та сонячні панелі можуть живити генератори для виробництва електроенергії в різних частинах бізнесу. Однак надворі немає ні вітру, ні сонця, а це означає, що вітрові турбіни та сонячні батареї не завжди здатні виробляти надійну електроенергію для електрогенераторів.

Компанії з відновлюваної енергетики обходять цю проблему шляхом підключення десятків тисяч вітряних турбін або сонячних панелей до однієї електромережі, що підвищує ймовірність того, що ці джерела енергії вироблятимуть надійну кількість енергії. енергії для мережі.

Також набагато легше передбачити, скільки енергії буде вироблено цими джерелами енергії, оскільки інженери можуть просто взяти очікуване середнє значення для десятків тисяч вітрових турбін або сонячних панелей.

Детальне пояснення цього явища можна знайти в цій статті Scientific American .