Розподіл парето
У цій статті пояснюється, що таке розподіл Парето в статистиці та для чого він використовується. Ви також зможете побачити графік розподілу Парето та властивості цього типу розподілу ймовірностей.
Що таке розподіл Парето?
Розподіл Парето — безперервний розподіл ймовірностей, який використовується в статистиці для моделювання принципу Парето. Таким чином, розподіл Парето є розподілом ймовірностей, який має кілька значень, ймовірність появи яких набагато вище, ніж інші значення.
Пам’ятайте, що закон Парето, також званий правилом 80-20, є статистичним принципом, який говорить, що більшість причин явища є причиною невеликої частини населення.
Розподіл Парето має два характерних параметри: параметр масштабу x m і параметр форми α.
Спочатку розподіл Парето використовувався для опису розподілу багатства всередині населення, оскільки більша частина його була зумовлена невеликою часткою населення. Але в даний час розподіл Парето має багато застосувань, наприклад, в контролі якості, в економіці, в науці, в соціальній сфері і т.д.
Розподіл Парето названо на честь економіста Вільфредо Парето, який сформулював розподіл. Однак найбільше він відомий завдяки діаграмі Парето.
Таблиця розподілу Парето
Тепер, коли ми знаємо визначення розподілу Парето, давайте розглянемо кілька прикладів розподілу Парето, представлених графічно.
Отже, нижче ви можете побачити, як виглядає графік функції щільності розподілу Парето в залежності від його характерних значень:
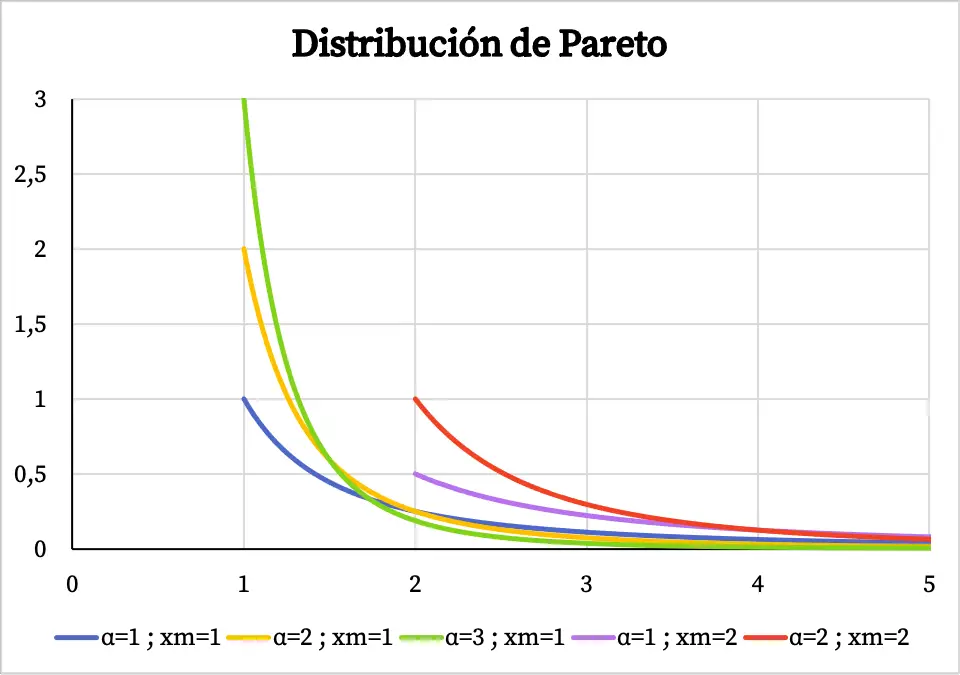
Зверніть увагу, що область розподілу Парето проходить від значення x m до +∞, тому функція щільності не існує до значення x m .
З іншого боку, графік кумулятивної функції ймовірності розподілу Парето має такий вигляд:
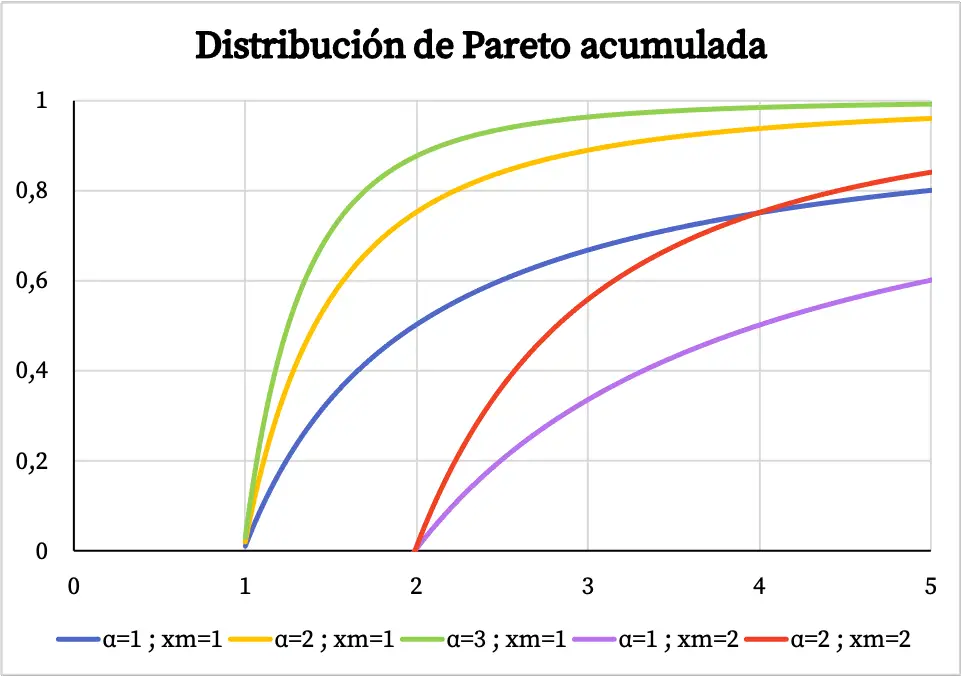
Характеристика розподілу Парето
Нижче наведено найважливіші характеристики розподілу Парето, пов’язані з теорією ймовірностей і статистикою.
- Розподіл Парето має два характерних параметри, які визначають його криву: параметр масштабу x m і параметр форми α.
- Область розподілу Парето складається з усіх дійсних чисел від параметра масштабу до плюс нескінченності.
- Якщо α більше за 1, середнє значення розподілу Парето дорівнює добутку α, помноженого на x m , і α мінус 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li> Дисперсія розподілу Парето залежить від двох характерних параметрів розподілу та обчислюється за такою формулою:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
![\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0dc2c772a0a0662ad05f8b22c3cf1ba1_l3.png "Rendered by QuickLaTeX.com")
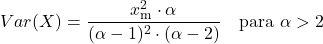
- Режим розподілу Парето еквівалентний масштабному параметру x m розподілу.
- Формула для функції густини розподілу Парето є:
![\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m](https://statorials.org/wp-content/ql-cache/quicklatex.com-1e182771cfe3bf9a145a2ee59b9c7eeb_l3.png "Rendered by QuickLaTeX.com")
- Подібним чином формула для кумулятивної функції ймовірності розподілу Парето має вигляд:
![\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha](https://statorials.org/wp-content/ql-cache/quicklatex.com-480adc7841b7c72cb4bfecb446ed3fab_l3.png "Rendered by QuickLaTeX.com")
- Коефіцієнт асиметрії розподілу Парето залежить лише від параметра форми α і має такий вираз:
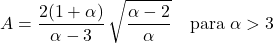
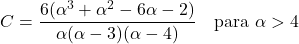
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше