Залежна змінна

У цій статті пояснюється, що таке залежні змінні. Таким чином, ви дізнаєтесь, що означає залежність змінної в математиці та статистиці, і, крім того, ви зможете побачити кілька прикладів залежних змінних.

Що таке залежна змінна?

Залежна змінна — це змінна, значення якої залежить від значення іншої змінної. Іншими словами, значення залежної змінної змінюватиметься залежно від значення незалежної змінної.

Загалом, залежна змінна зазвичай позначається літерою y на осі y (вертикальна вісь).

Наприклад, ціна акцій є залежною змінною, яка залежить від багатьох інших змінних, таких як економічний результат компанії, кількість інвесторів, останні новини компанії тощо.

Приклади залежних змінних

Тепер, коли ми знаємо визначення залежної змінної, ми побачимо кілька прикладів цього типу змінної, щоб повністю зрозуміти концепцію.

• Здоров’я людини (залежна змінна) залежить від її раціону (незалежна змінна).
• Частота серцевих скорочень людини (залежна змінна) залежить від того, наскільки вона висока (незалежна змінна).
• Рівень задоволеності клієнта (залежна змінна) змінюється залежно від якості наданої послуги (незалежна змінна).
• Кількість забруднюючих речовин, які викидає країна (залежна змінна), залежить від промислового виробництва цієї країни (незалежна змінна).
• Зарплата таксиста (залежна змінна) змінюється в залежності від кількості поїздок, які він здійснює (незалежна змінна).

Залежна змінна в математиці

У математиці причинно-наслідковий зв’язок зазвичай моделюється за допомогою незалежної змінної та залежної змінної. Таким чином, функція визначає математичне співвідношення, яке існує між залежною змінною та незалежною змінною.

Залежні змінні зазвичай позначаються буквою y , з іншого боку, літера x зазвичай використовується для позначення незалежних змінних.

Наприклад, функція y=2x вказує, що коли незалежна змінна x збільшується на одну одиницю, залежна змінна y збільшується вдвічі більше.

Щоб дізнатися більше про математичні функції, ви можете відвідати веб-сайт нашого партнера, function.xyz .

Залежна змінна в статистиці

Однак насправді дуже важко знайти зв’язок між двома змінними, який можна визначити точною математичною функцією, тому що іноді те саме значення незалежної змінної призводить до іншого значення залежної змінної.

Наприклад, іноді, навчаючись більше, ми отримуємо нижчу оцінку або, навпаки, навчаючись менше, ми отримуємо кращу оцінку. Тому кількість годин, які ми присвячуємо навчанню, не є єдиним фактором, який впливає на отриману оцінку, вона також може змінюватися залежно від складності іспиту або складності матеріалу, що вивчається.

З цієї причини в статистиці зазвичай проводять багато експериментів, щоб визначити, чи існує зв’язок між двома змінними, одна з яких буде незалежною змінною, а інша – залежною. Потім отримані результати можна представити графічно, щоб перевірити, чи зв’язані змінні, і, якщо так, побачити, який тип зв’язку вони мають (позитивний, негативний, лінійний, експоненціальний тощо).

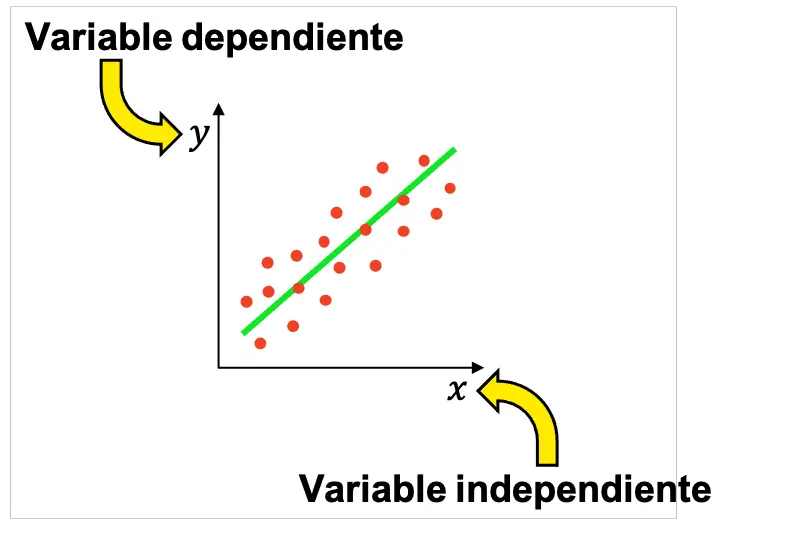
Майте на увазі, що в опитуванні може бути більше однієї незалежної змінної, хоча основні статистичні дослідження проводяться з однією незалежною та однією залежною змінною.

Після проведення статистичного дослідження можна обчислити математичну функцію, щоб зробити наближення та таким чином змоделювати зв’язок між змінними. Тому зазвичай спочатку створюється статистична модель, а потім — математична.