Що таке залишковий розрив? (визначення & #038; приклад)

Залишкова дисперсія (іноді її називають «непоясненою дисперсією») відноситься до дисперсії в моделі, яку не можна пояснити змінними моделі.

Чим вище залишкова дисперсія моделі, тим менше модель здатна пояснити варіацію в даних.

Залишкова дисперсія з’являється в результатах двох різних статистичних моделей:

1. ANOVA: використовується для порівняння середніх трьох або більше незалежних груп.

2. Регресія: використовується для кількісного визначення зв’язку між однією або декількома змінними предиктора та змінною відповіді .

У наступних прикладах показано, як інтерпретувати залишкову дисперсію в кожному з цих методів.

Залишкова дисперсія в моделях ANOVA

Щоразу, коли ми підбираємо модель ANOVA («дисперсійний аналіз»), ми отримуємо таблицю ANOVA, яка виглядає так:

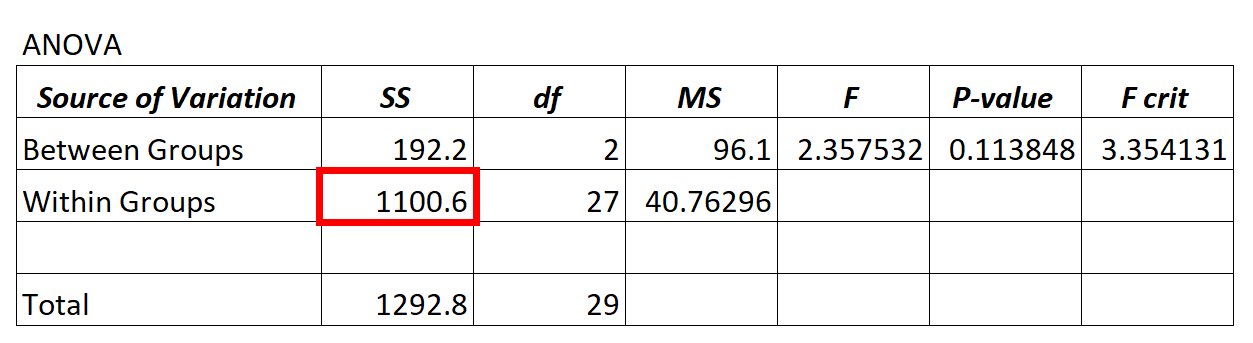
Значення залишкової дисперсії з моделі ANOVA знаходиться в стовпці SS («сума квадратів») для варіації всередині групи .

Це значення також називається «сумою квадратів помилок» і обчислюється за такою формулою:

Σ(X _ij – X _j ) ²

золото:

• Σ : грецький символ, що означає «сума»
• X _ij : ^i-те спостереження групи j
• X _j : середнє значення групи j

У наведеній вище моделі ANOVA ми бачимо, що залишкова дисперсія становить 1100,6.

Щоб визначити, чи є ця залишкова дисперсія «високою», ми можемо обчислити середню суму квадратів для груп і середню суму квадратів для груп і знайти співвідношення між ними, яке дає загальне значення F у таблиці ANOVA.

• F = MS _{входить} / MS _{входить}
• F = 96,1 / 40,76296
• F = 2,357

Значення F у таблиці ANOVA вище становить 2,357, а відповідне значення p — 0,113848. Оскільки це p-значення не менше α = 0,05, ми не маємо достатніх доказів, щоб відхилити нульову гіпотезу.

Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що середня різниця між групами, які ми порівнюємо, значно відрізняється.

Це говорить нам про те, що залишкова дисперсія моделі ANOVA висока порівняно з варіацією, яку модель може фактично пояснити.

Залишкова дисперсія в регресійних моделях

У регресійній моделі залишкова дисперсія визначається як сума квадратів різниць між прогнозованими точками даних і спостережуваними точками даних.

Він розраховується таким чином:

Σ(ŷ _i – y _i ) ²

золото:

• Σ : грецький символ, що означає «сума»
• ŷ _i : прогнозовані точки даних
• y _i : спостережувані точки даних

Коли ми підбираємо регресійну модель, ми зазвичай отримуємо результат, який виглядає так:

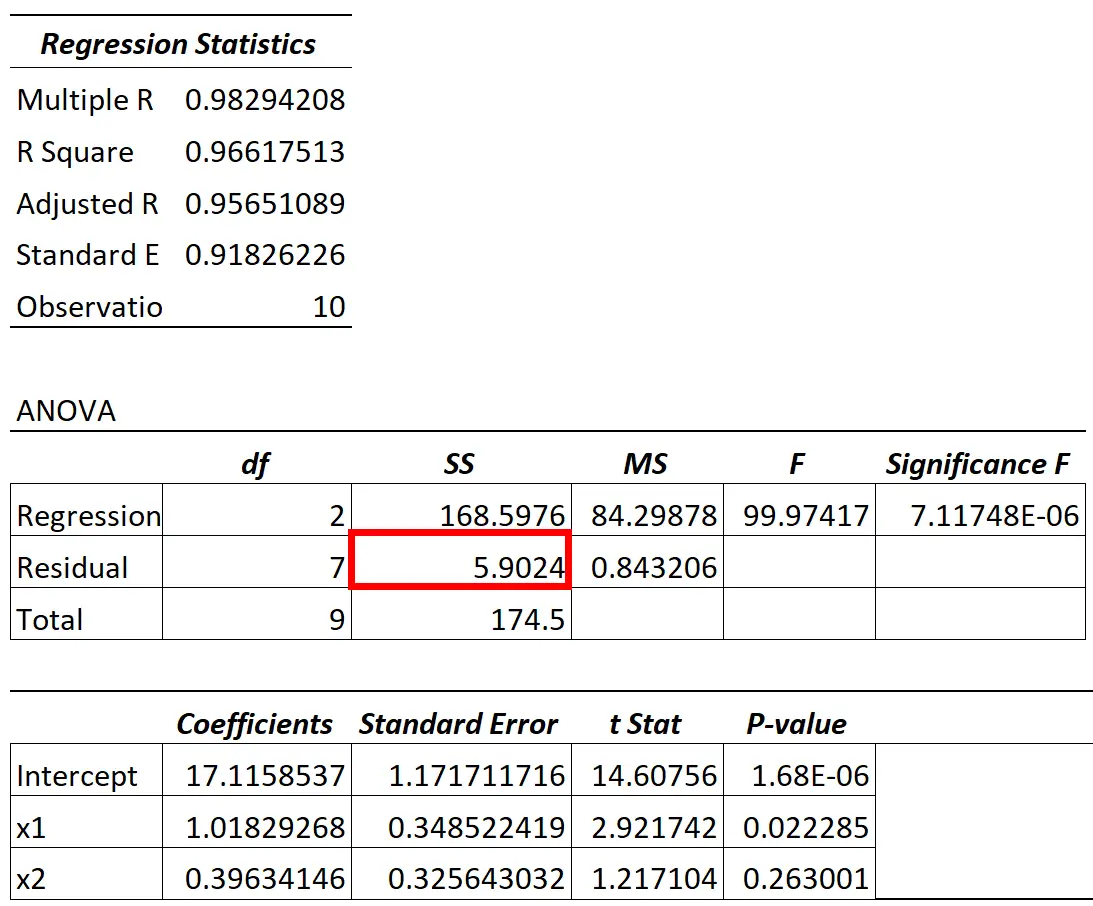
Значення залишкової дисперсії з моделі ANOVA можна знайти в стовпці SS («сума квадратів») для залишкової варіації.

Співвідношення залишкової варіації до загальної варіації в моделі говорить нам про відсоток варіації у змінній відповіді, який не можна пояснити змінними предиктора в моделі.

Наприклад, у таблиці вище ми розрахуємо цей відсоток таким чином:

• Непояснена варіація = SS Residual / SS Total
• Непояснена варіація = 5,9024 / 174,5
• Непояснена варіація = 0,0338

Це значення також можна розрахувати за такою формулою:

• Непояснена варіація = 1 – R ²
• Непояснена варіація = 1 – 0,96617
• Непояснена варіація = 0,0338

Значення R-квадрат моделі повідомляє нам про відсоток варіації змінної відповіді, який можна пояснити змінною предиктора.

Таким чином, чим нижча незрозуміла варіація, тим більша здатність моделі використовувати прогностичні змінні для пояснення варіації змінної відповіді.

Додаткові ресурси

Що таке хороше значення R-квадрат?
Як розрахувати R-квадрат в Excel
Як обчислити R-квадрат у R